Нет, это статья не о графах с титулами и дворцами. Речь пойдет о графах из мира математики — тех самых, что состоят из точек и линий между ними. Мы разберемся, что такое графы в контексте дискретной математики, где и как они применяются. Познакомимся с их основными видами и попробуем решить несколько занимательных задач.
Что такое графы и зачем они нужны
Графы — одно из фундаментальных понятий математики. В самом простом представлении граф — это множество точек, соединенных линиями. Точки называются вершинами графа, а линии — ребрами. Также вершины могут называться узлами, а ребра — связями. Вот так может выглядеть граф:
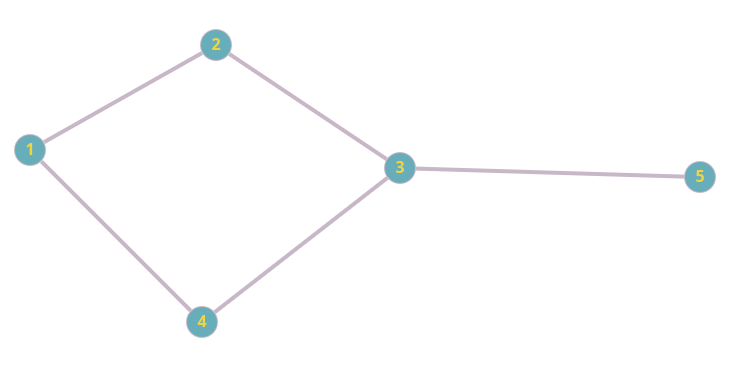
В дискретной математике существует целый раздел, посвященный изучению графов. Он называется теорией графов и считается одной из ветвей топологии.
С математической точки зрения граф — это совокупность двух множеств. Одно из них — множество вершин, другое — множество ребер. Каждый элемент из множества ребер представляет собой пару элементов из множества вершин.
Граф — это топологический объект, а не геометрический: он не изменится, если изменить его размеры или масштаб отдельных его частей. Он останется тем же графом — с теми же вершинами и ребрами. Важна не форма, а структура: какие вершины и как связаны между собой. Для сравнения, если изменить длину стороны у треугольника — геометрического объекта — мы получим уже другой треугольник.
Графы нашли широкое применение в современной науке и технике. Их используют в физике, химии, социологии, информатике и многих других дисциплинах. С помощью графов удобно анализировать взаимосвязи между объектами и внутренние связи внутри сложных систем. Именно поэтому графы широко применяются в сетевых технологиях, например, для описания компьютерных сетей. Кроме того, они используются при анализе маршрутов транспортных сообщений — например, для оптимизации авиаперелетов или автобусных рейсов.
Вершины и ребра
Вершина графа — это точка, представляющая какой-либо объект. В топологической модели графа не имеют значения ни координаты вершины, ни ее размер или расположение.
Ребро графа — это неупорядоченная пара вершин, связанных друг с другом. Такие вершины называются концевыми.
Инцидентность — одно из ключевых понятий в теории графов. Вершина называется инцидентной ребру, если она является одной из его концевых вершин.
Рассмотрим следующий граф:
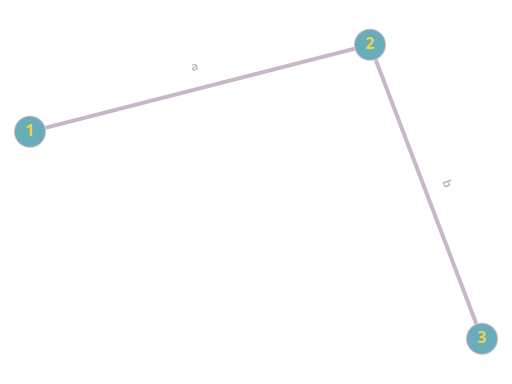
В этом графе вершины 1 и 2 инцидентны ребру a, так же как вершины 2 и 3 инцидентны ребру b. Кроме того, ребра a и b инцидентны вершине 2. Отдельно можно отметить, что вершина 2 инцидентна ребру b, а ребро a, помимо вершины 2, инцидентно также вершине 1 — как и ребро b инцидентно вершине 3.
Еще одно важное понятие — смежность вершин и ребер. Если две вершины инцидентны одному и тому же ребру, они называются смежными. Аналогично, если два ребра инцидентны одной вершине, они также считаются смежными.
В приведенном графе вершины 1 и 2 — смежные, как и вершины 2 и 3. Ребра a и b также являются смежными, поскольку обе инцидентны вершине 2.
Петля — это ребро, инцидентное одной и той же вершине дважды. Пример:

Ребра могут быть кратными (параллельными), то есть имеющими одинаковые концевые вершины:

Степень вершины — это количество ребер, инцидентных данной вершине. Другими словами, это число ребер, исходящих из этой вершины.
Вершина может быть изолированной — в этом случае ее степень равна нулю, так как она не соединена ни с одной другой вершиной. У так называемой висячей вершины степень равна единице — к ней подсоединено только одно ребро.
Рассмотрим следующий граф:
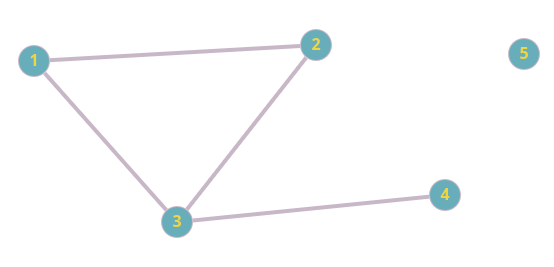
Степени вершин 1 и 2 равны двум, а степень вершины 3 — трем. Вершина 4 является висячей, так как ее степень равна единице. Вершина 5 — изолированная, поскольку ее степень равна нулю.
Все рассмотренные выше графы имеют неориентированные ребра, то есть ребра без направления. Однако ребра могут быть и ориентированными — такие ребра называются дугами. Вот пример графа с ориентированными ребрами:
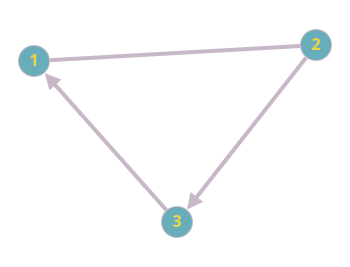
Как видно, в этом графе два ориентированных ребра (1-3 и 2-3) и одно неориентированное (1-2).
Какие бывают графы
Графы бывают самые разные. Рассмотрим некоторые разновидности графов.
Псевдографы и мультиграфы
Ранее мы упоминали петли и кратные ребра. Графы, содержащие петли, называются псевдографами, а графы с кратными ребрами — мультиграфами. Если в графе присутствуют и петли, и кратные ребра, такой граф называют псевдомультиграфом.
Граф, в котором нет ни петель, ни кратных ребер, называется простым графом.
Вот пример псевдомультиграфа:
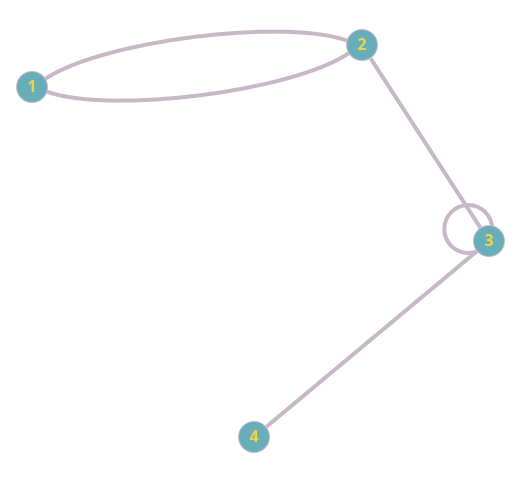
Ориентированные и неориентированные графы
Граф, в котором все ребра имеют направление, называется ориентированным. Такой граф еще называют орграфом. Если все ребра — без направления, то граф называется неориентированным.
Если же в графе одновременно присутствуют как направленные, так и ненаправленные ребра, то он называется смешанным графом.
Пример ориентированного графа:
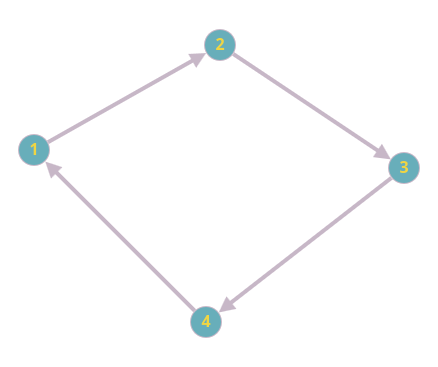
Полные и регулярные графы
Граф называется полным, если каждая пара его вершин соединена одним ребром. Пример:
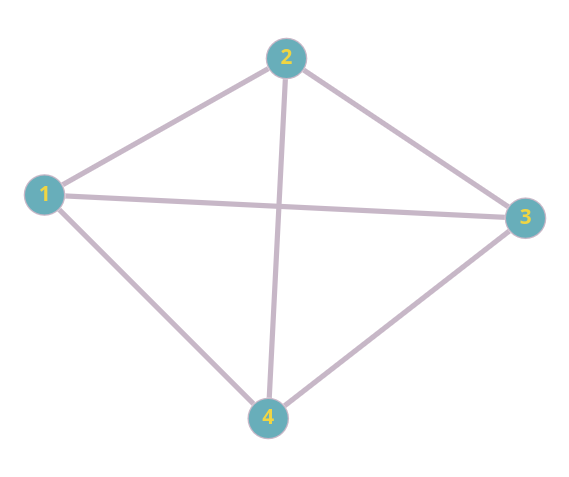
То есть в таком графе, если и добавлять новые соединения, то сделать это можно только с помощью петель или кратных ребер — другие варианты нарушат его простоту.
Существует еще одно важное понятие — регулярный граф. Это граф, в котором все вершины имеют одинаковую степень. Примером регулярного графа является показанный выше полный граф, а также, например, ориентированный граф из предыдущего раздела, если каждая вершина в нем имеет одинаковое количество входящих и исходящих дуг.
Пустой граф
Пустой граф — это граф без ребер, то есть состоящий из одних вершин:
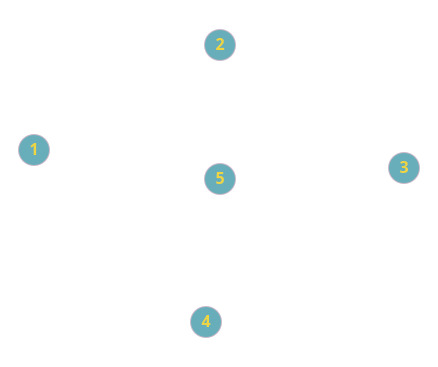
Для чего может понадобиться такой граф? Например, для того, чтобы показать, что какие-либо объекты никак не связаны друг с другом.
Планарный граф
Планарным графом называют такой граф, который можно изобразить на плоскости так, чтобы его ребра пересекались только в вершинах, то есть нигде не пересекались между собой вне узлов.
Вот пример планарного графа:
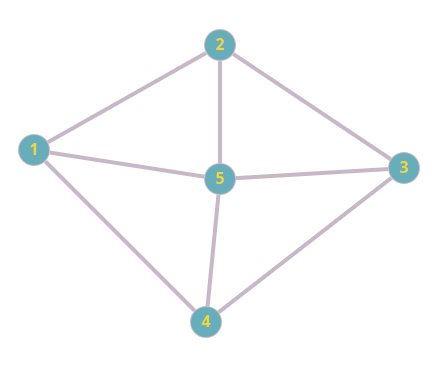
Двудольный граф
Если вершины графа можно разделить на две группы так, что ребра соединяют только вершины из разных групп, а внутри каждой группы соединений нет, то такой граф называется двудольным.
Вот пример двудольного графа:
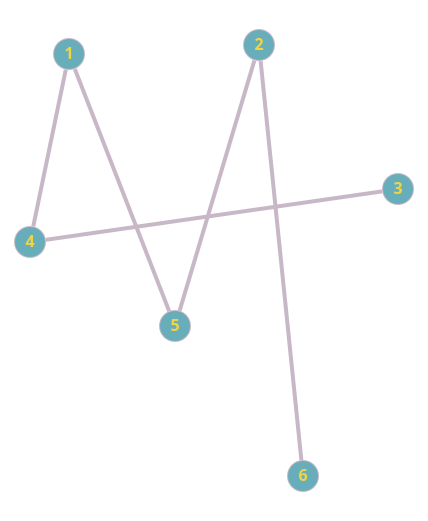
Здесь мы видим две группы вершин. Одна группа включает вершины 1, 2 и 3, другая — вершины 4, 5 и 6. Связи существуют только между вершинами, принадлежащими разным группам. Внутри самих групп вершины никак не связаны между собой.
Взвешенные графы
Взвешенными называют графы, в которых каждому ребру сопоставлено числовое значение, называемое весом. Вес может отражать расстояние, время в пути, скорость передачи данных или любую другую значимую величину, связанную со связью между вершинами.
Вот пример взвешенного графа:
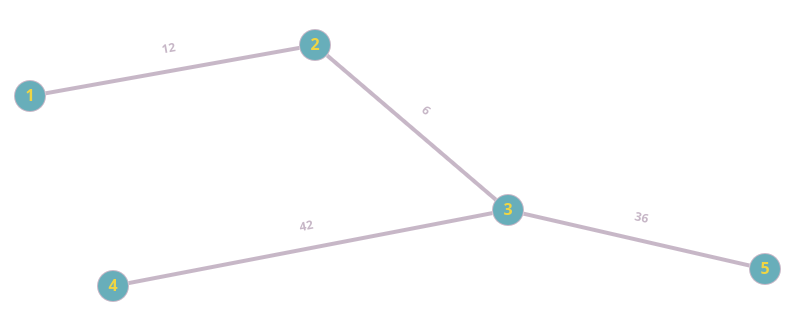
Деревья
Еще одна интересная разновидность графов — это деревья. Прежде чем говорить о деревьях введем следующие понятия:
- Путь — это последовательность смежных ребер.
- Цепь — это путь без повторяющихся ребер.
- Цикл — это такая цепь, в которой последняя вершина совпадает с первой.
- Связный граф — это такой граф, в котором существует путь между любой парой вершин.
Дерево — это связный граф без циклов.
Граф можно назвать деревом, если в нем выполняются следующие условия:
- Если взять любую пару вершин, то между ними можно проложить один единственный путь.
- В дереве количество ребер на единицу меньше количества вершин.
- Хотя бы одна из вершин в дереве должна быть висячей.
- Нет замкнутых областей (циклов).
Пример дерева:
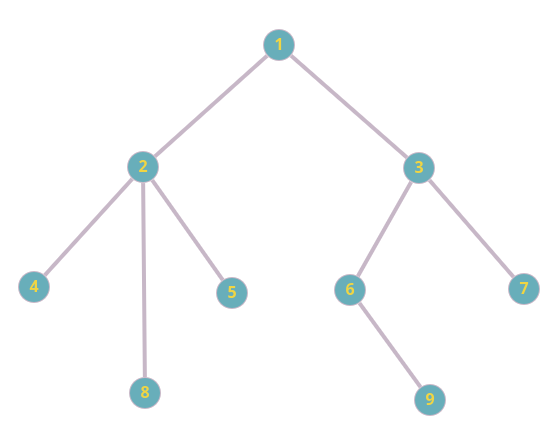
Изображенное выше дерево называется корневым деревом. Вершина 1 — это корень дерева. Она также является родительской вершиной для вершин 2 и 3. В свою очередь, вершины 2 и 3 являются потомками вершины 1.
Существует также особый тип деревьев — бинарные деревья. Это такие деревья, в которых каждая вершина имеет не более двух потомков.
Вот пример бинарного дерева:
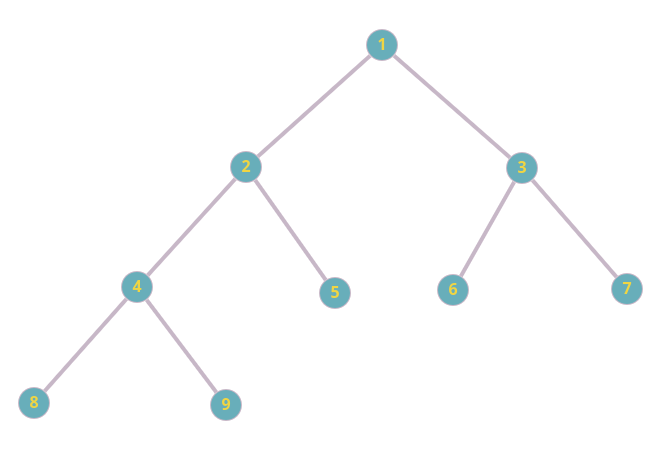
У бинарных деревьев степень вершины не может быть больше трех.
Задачи с графами
С помощью графов можно решать различные интересные задачки.
Задача 1
Решим, например, такую задачу: Требуется узнать сколько разных трехзначных чисел можно записать при помощи цифр 0 и 1.
Составим граф. Так как числа нужны трехзначные, то разделим его на три группы. Первая группа — группа сотен, вторая группа представляет десятки и третья — единицы. Соединим вершины, учитывая, что число не может начинаться с нуля:
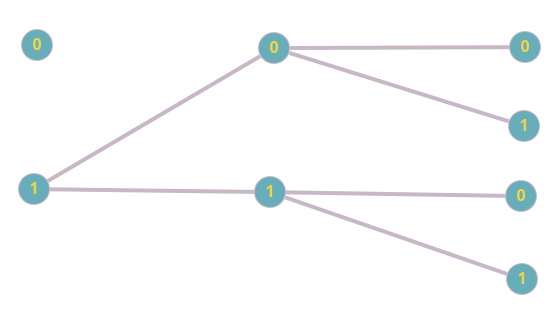
Получился граф (бинарное дерево) с одной изолированной вершиной. Как видно, можно составить только 4 трехзначных числа используя 0 и 1. Это числа 100, 101, 110 и 111.
Задача 2
Решим еще одну задачу. Пусть даны пять университетских футбольных команд. Каждая команда сыграла с другой по одному матчу. Требуется узнать сколько всего матчей было сыграно.
Для решения этой задачи нам понадобится составить полный граф с пятью вершинами:
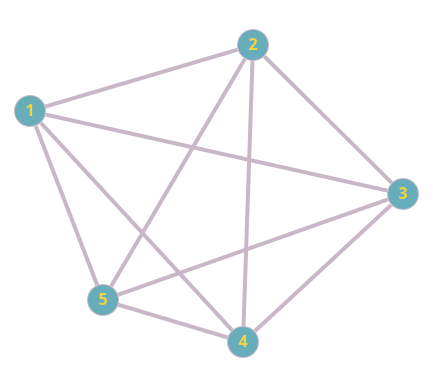
Подсчитаем количество ребер в графе. Это можно сделать вручную, но можно воспользоваться следующей формулой:
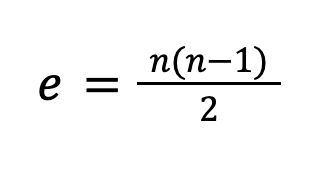
В этой формуле e — количество ребер, а n — количество вершин. Подставим в формулу число 5 и получим:
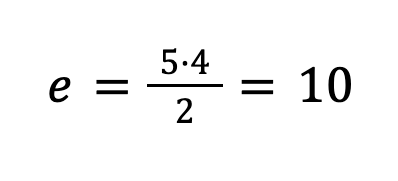
То есть, всего было сыграно 10 матчей.
Задача 3
Еще одна задача. На участке растут 8 деревьев: тополь, яблоня, береза, рябина, дуб, лиственница, клен и сосна. Известно, что яблоня выше клена, рябина выше лиственницы, дуб ниже березы, но выше сосны, береза ниже тополя, сосна выше рябины, а лиственница выше яблони. Требуется расположить деревья от самого высокого до самого низкого.
Здесь мы будем использовать ориентированный граф. Вершины графа будут представлять деревья, а ребра — отношения высоты. Если известно, что яблоня выше клена, то мы ориентируем ребро от яблони в сторону клена, то есть от низкого дерева к более высокому. Таким образом получаем такой граф:
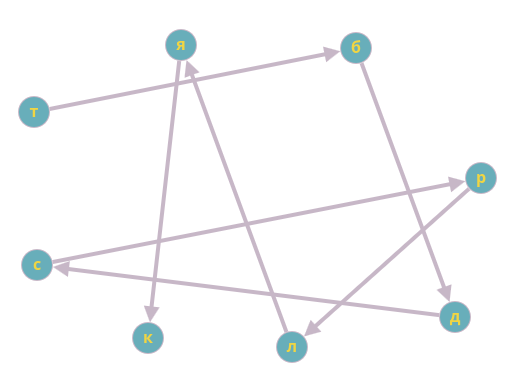
Итак, в порядке уменьшения высоты деревья располагаются следующим образом: тополь, береза, дуб, сосна, рябина, лиственница, яблоня, клен.
Подведем итоги
- Графы — важное понятие в дискретной математике. Граф можно представить как совокупность множества вершин и множества ребер.
- Графы широко применяются в науке и технике. С их помощью можно моделировать и изучать связи между объектами.
- Среди разновидностей графов можно назвать полные, регулярные, псевдографы, двудольные графы и другие.
- С помощью графов можно решать разнообразные интересные задачи.