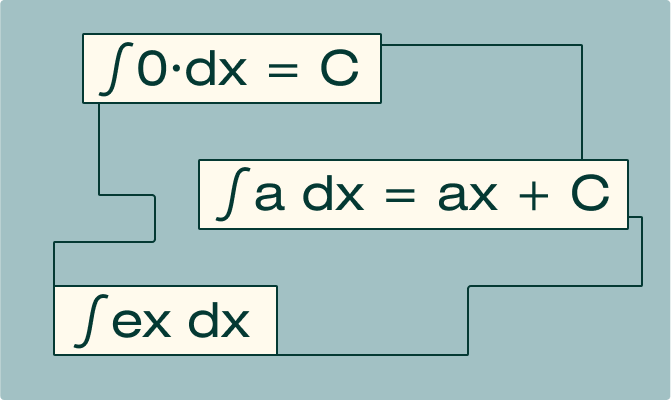Что такое интегралы: от площади под кривой до машинного обучения

Интегралы — это мощнейший инструмент как в классической математике, так и в машинном обучении. Многие помнят их со школы или университета как что-то, связанное с поиском «площади под кривой», но зачем это нужно на практике, особенно в ML? Давайте разбираться.

Что такое интеграл в математике и зачем он нужен

Представьте, что вы едете на машине и ваш спидометр постоянно показывает разную скорость. Как узнать, какое общее расстояние вы проехали за час? Если бы скорость была постоянной (скажем, 60 км/ч), все просто: 60 км/ч * 1 час = 60 км. Но скорость менялась!

Интеграл — это математический инструмент, который позволяет нам суммировать бесконечно много бесконечно малых величин. В примере с машиной мы могли бы разбить час на миллионы крошечных интервалов времени. В каждый такой момент скорость почти постоянна. Умножив эту «почти постоянную» скорость на крошечный промежуток времени, мы получим микроскопическое расстояние, пройденное за этот момент. Интеграл — это способ сложить все эти микрорасстояния, чтобы получить точное общее расстояние.

Проще говоря, интеграл помогает найти:

• площадь фигуры сложной формы (та самая «площадь под кривой»);
• объем тел вращения;
• общее изменение какой-либо величины, если мы знаем скорость ее изменения (как в примере с машиной);
• среднее значение функции на отрезке;
• вероятности в теории вероятностей и статистике (очень важно для ML!). Например, площадь под кривой плотности распределения вероятности дает нам вероятность попадания случайной величины в определенный интервал.

В ML интегралы неявно всплывают при работе с непрерывными распределениями вероятностей, при вычислении математического ожидания, в некоторых методах оптимизации и при анализе моделей. Понимание интегралов дает более глубокое видение этих процессов.

Как работает интеграл

Вернемся к площади под кривой. Представьте график какой-то функции, скажем, y = x². Как найти площадь под этим графиком от x = 0 до x = 2?

Идея, лежащая в основе интеграла (спасибо Ньютону и Лейбницу!), гениальна в своей простоте:

1. Разбиваем отрезок (от 0 до 2) на множество очень узких вертикальных столбиков (прямоугольников).
2. Ширина каждого столбика — крошечная величина (назовем ее Δx).
3. Высота каждого столбика примерно равна значению функции y = x² в этой точке.
4. Площадь одного такого столбика: высота * ширина ≈ f(x) * Δx.
5. Суммируем площади всех этих столбиков: Σ f(x) * Δx.

А теперь фокус: если мы сделаем эти столбики бесконечно узкими (Δx стремится к нулю), то наша сумма площадей столбиков станет точно равна площади под кривой. Этот предел суммы и есть интеграл.

Математически это записывается символом ∫, который похож на вытянутую букву S (от слова “Sum” — сумма).

Для чего нужен дифференциал

В записи интеграла, например ∫ f(x)dx, вы видите dx. Это и есть дифференциал. Что он означает?

Помните наши бесконечно узкие столбики из предыдущего пункта? dx — это и есть та самая бесконечно малая ширина столбика. Он указывает:

1. по какой переменной мы «суммируем» (интегрируем). В данном случае — по x;
2. бесконечно малую величину, на которую мы умножаем значение функции f(x), чтобы получить «площадь» бесконечно тонкого столбика f(x)dx.

Дифференциал тесно связан с понятием производной. Если производная f'(x) показывает мгновенную скорость изменения функции f(x), то дифференциал dy = f'(x) dx показывает бесконечно малое изменение функции y = f(x), соответствующее бесконечно малому изменению аргумента dx. В контексте интеграла dx просто говорит нам: «Мы суммируем бесконечно малые кусочки вдоль оси X».

Что такое неопределенный интеграл

А вот здесь начинается самое интересное! Неопределенный интеграл — это операция, обратная дифференцированию (нахождению производной).

Если производная отвечает на вопрос «Какова скорость изменения этой функции?», то неопределенный интеграл отвечает: «Какая функция имеет вот такую скорость изменения?»

Например, мы знаем, что производная функции y = x² равна y’ = 2x. Тогда неопределенный интеграл от 2x будет равен x². Записывается это так: ∫ 2x dx = x².

Но есть нюанс! Производная от x² + 5 тоже равна 2x. И производная от x² − 100 тоже равна 2x. Производная любой константы равна нулю!

Поэтому, когда мы берем неопределенный интеграл, мы не можем точно знать, какая константа была у исходной функции. Мы обозначаем эту неизвестную константу как + C (константа интегрирования).

Правильно: ∫ 2x dx = x² + C.

Неопределенный интеграл дает нам не одну конкретную функцию, а целое семейство функций (первообразных), которые отличаются друг от друга на константу.

Таблица интегралов элементарных функций

«Полная» таблица интегралов — это как «полный» словарь языка, она огромна. Но для большинства задач, особенно на начальном этапе, достаточно знать несколько основных интегралов, которые получаются обращением правил дифференцирования. Вот самые ходовые:

• Интеграл от нуля: ∫ 0 dx = C
• Интеграл от константы: ∫ k dx = kx + C (где k — число)
• Степенная функция: ∫ xⁿ dx = (xⁿ⁺¹ / (n+1)) + C (при n ≠ −1)
  • Пример: ∫ x² dx = (x³ / 3) + C
  • Пример: ∫ √x dx = ∫ x¹ᐟ² dx = (x³/² / (3/2)) + C = (2/3)x√x + C

• Интеграл от 1/x: ∫ (1/x) dx = ∫ x⁻¹ dx = ln|x| + C (здесь n = −1, поэтому степенное правило не работает!)
• Экспонента:
  • ∫ eˣ dx = eˣ + C
  • ∫ aˣ dx = (aˣ / ln a) + C
• Тригонометрические функции:
  • ∫ sin(x) dx = −cos(x) + C
  • ∫ cos(x) dx = sin(x) + C
  • ∫ (1/cos²(x)) dx = tg(x) + C
  • ∫ (1/sin²(x)) dx = −ctg(x) + C

Этого набора обычно хватает для решения 80% задач на первых порах. Более сложные интегралы часто сводятся к табличным с помощью различных методов (замена переменной, интегрирование по частям).

Математические свойства интегралов

Интегралы обладают удобными свойствами, которые сильно упрощают вычисления:

1. Вынесение константы за знак интеграла: ∫ k * f(x) dx = k * ∫ f(x) dx

• Пример: ∫ 5x² dx = 5 * ∫ x² dx = 5 * (x³/3) + C
• Аналогия: Если вы едете в пять раз быстрее, то и расстояние за то же время проедете в пять раз больше.

2. Интеграл суммы/разности: ∫ (f(x) ± g(x)) dx = ∫ f(x) dx ± ∫ g(x) dx

• Пример: ∫ (x² + cos(x)) dx = ∫ x² dx + ∫ cos(x) dx = (x³/3) + sin(x) + C (rонстанту C достаточно написать один раз в конце).
• Аналогия: Если общее количество воды в бассейне складывается из потока из двух труб, то и общий объем равен сумме объемов из каждой трубы.

Эти два свойства (линейность интеграла) позволяют нам разбивать сложные функции на более простые части и интегрировать их по отдельности.

Что такое определенный интеграл

Если неопределенный интеграл — это семейство функций (антипроизводная + C), то определенный интеграл — это конкретное число.

Определенный интеграл ∫[a, b] f(x) dx (читается «интеграл от a до b f(x) dx») вычисляет ту самую чистую площадь под графиком функции f(x) между вертикальными линиями x = a и x = b.

• a — нижний предел интегрирования.
• b — верхний предел интегрирования.

Как его вычислить? Здесь нам на помощь приходит формула Ньютона–Лейбница (основа интегрального исчисления):

1. Найдите одну из первообразных F(x) для функции f(x) (т. е. возьмите неопределенный интеграл, но константу C можно опустить, она все равно сократится).
2. Вычислите значение первообразной в верхней точке: F(b).
3. Вычислите значение первообразной в нижней точке: F(a).
4. Вычтите второе из первого: ∫[a, b] f(x) dx = F(b) − F(a).

Пример из жизни: Если f(t) — это скорость потока воды в литрах в секунду, то ∫[t₁, t₂] f(t) dt даст нам точное количество литров воды, которое вытекло из трубы за время от t₁ до t₂. Это уже не формула зависимости объема от времени, а конкретное число литров.

Примеры математического вычисления интегралов

Давайте применим наши знания.

Пример 1: Неопределенный интеграл

Найти ∫ (3x² − 4x + 5) dx.

1. Используем свойство суммы/разности: ∫ 3x² dx − ∫ 4x dx + ∫ 5 dx
2. Выносим константы: 3 ∫ x² dx — 4 ∫ x¹ dx + 5 ∫ x⁰ dx (помним, что x⁰ = 1)
3. Применяем формулу для степенной функции ∫ xⁿ dx = xⁿ⁺¹ / (n + 1): 3 * (x³/3) − 4 * (x²/2) + 5 * (x¹/1) + C
4. Упрощаем: x³ − 2x² + 5x + C

Проверка: Возьмем производную от x³ − 2x² + 5x + C. Получим (x³)’ − (2x²)’ + (5x)’ + (C)’ = 3x² − 4x + 5 + 0. Совпало с исходной функцией под интегралом!

Пример 2: Определенный интеграл

Вычислить ∫[1, 2] (3x² − 4x + 5) dx.

1. Мы уже нашли первообразную в предыдущем примере: F(x) = x³ − 2x² + 5x. (Константу C можно опустить.)
2. Вычисляем F(b), то есть F(2) :  F(2) = (2)³ − 2*(2)² + 5*(2) = 8 − 2*4 + 10 = 8 − 8 + 10 = 10
3. Вычисляем F(a), то есть F(1) :  F(1) = (1)³ − 2*(1)² + 5*(1) = 1 − 2*1 + 5 = 1 − 2 + 5 = 4
4. Применяем формулу Ньютона-Лейбница F(b) − F(a) : ∫[1, 2] (3x² − 4x + 5) dx = F(2) − F(1) = 10 − 4 = 6

Ответ: 6. Это число — площадь под параболой y = 3x² − 4x + 5 на отрезке от x = 1 до x = 2.

Пример вычисления интегралов на Python

Вручную считать интегралы бывает утомительно, особенно для сложных функций. К счастью, у нас есть Python и его замечательные библиотеки!

Основные инструменты:

• SymPy: для символьных вычислений (как мы делали на бумаге, получает точную формулу или значение).
• SciPy: для численных вычислений (получает приближенное числовое значение, полезно, когда аналитическое решение найти сложно или невозможно).

import sympy
import scipy.integrate as spi
import numpy as np

# --- Символьные вычисления с SymPy ---

# Определяем символьную переменную
x = sympy.symbols('x')

# Определяем функцию
f_sym = 3*x**2 - 4*x + 5

# 1. Неопределенный интеграл
indefinite_integral = sympy.integrate(f_sym, x)
print(f"Неопределенный интеграл (SymPy): {indefinite_integral}")
# Вывод: Неопределенный интеграл (SymPy): x**3 - 2*x**2 + 5*x
# (SymPy по умолчанию не пишет + C, но мы помним!)

# 2. Определенный интеграл
definite_integral_sym = sympy.integrate(f_sym, (x, 1, 2)) # (переменная, ниж_предел, верх_предел)
print(f"Определенный интеграл (SymPy): {definite_integral_sym}")
# Вывод: Определенный интеграл (SymPy): 6
# (Результат совпал с ручным расчетом!)


# --- Численные вычисления с SciPy ---

# Определяем функцию как Python-функцию (для SciPy)
def f_num(x_val):
  return 3*x_val**2 - 4*x_val + 5

# 3. Определенный интеграл (численно)
# scipy.integrate.quad(функция, ниж_предел, верх_предел)
# Возвращает кортеж: (приближенное значение интеграла, оценка погрешности)
definite_integral_num, error_estimate = spi.quad(f_num, 1, 2)

print(f"Определенный интеграл (SciPy численно): {definite_integral_num}")
print(f"Оценка погрешности (SciPy): {error_estimate}")
# Вывод:
# Определенный интеграл (SciPy численно): 6.0
# Оценка погрешности (SciPy): 6.661338147750939e-14 (очень маленькая ошибка)

# Пример с функцией, которую сложно взять вручную (численно)
def hard_func(x_val):
    return np.exp(-x_val**2) * np.sin(x_val)**2

integral_hard_num, _ = spi.quad(hard_func, -np.inf, np.inf) # Интеграл от -inf до +inf
print(f"Численный интеграл от exp(-x^2)*sin(x)^2 по всей оси: {integral_hard_num}")
# Этот интеграл аналитически тоже берется, но численно - проще.
# SciPy отлично справляется с такими задачами.

Неопределенный интеграл (SymPy): x3 – 2*x2 + 5*x
Определенный интеграл (SymPy): 6
Определенный интеграл (SciPy численно): 6.0
Оценка погрешности (SciPy): 6.661338147750939e-14
Численный интеграл от exp(-x^2)*sin(x)^2 по всей оси: 0.5602022593661148

Как видите, Python позволяет легко вычислять как точные (символьные), так и приближенные (численные) значения интегралов. В ML чаще используются численные методы, так как мы работаем с данными и сложными моделями, где аналитические формулы получить трудно.

Коротко об интегралах

• Интеграл — это мощный инструмент для «суммирования» бесконечно малых величин, позволяющий находить площади, объемы, общие изменения и многое другое.
• Неопределенный интеграл — операция, обратная производной, дающая семейство функций (+ C).
• Определенный интеграл — это конкретное число, равное чистой площади под кривой между двумя пределами.
• Дифференциал dx указывает, по какой переменной мы интегрируем и что ширина «столбика» бесконечно мала.
• Интегралы обладают свойствами, упрощающими вычисления (линейность).
• Python (SymPy, SciPy) — отличный помощник для вычисления интегралов.