Математический анализ нужен не только ученым. Его используют в программировании, экономике, инженерии и других сферах.
В статье разберем основные понятия матанализа, расскажем, зачем он нужен и кому стоит его изучать.
Что такое матанализ
Математический анализ — комплекс разделов математики, который изучает функции, их параметры и изменения. Он также помогает понять сложные концепции других математических направлений, например дискретной математики, математической кибернетики и теории вероятностей.
Матанализ нужен разным специалистам, от физиков до программистов. Например, с его помощью оценивают время реализации алгоритмов или оптимизируют процесс машинного обучения.
В широком смысле математический анализ состоит из двух разделов:
- Интегральное исчисление изучает интегралы — они описывают, какие значения функция приобретает за определенное время. Раздел применяется для подсчета массы, объема и других величин, а также анализа вероятностей.
- Дифференциальное исчисление изучает производные — они показывают скорость изменения функции по ее входным параметрам. Раздел используется для оптимизации и моделирования процессов, а также анализа данных.
История развития матанализа
Принято считать, что математический анализ зародился в 17 веке. В середине 17 века Рене Декарт опубликовал свой труд «Геометрия», где описал аналитический метод координат. Это подтолкнуло ученых к разработке задач на языке числовых функций. Над этим работали Пьер Ферма, Блез Паскаль и другие математики.
Метод анализа параллельно изобрели двое ученых — Исаак Ньютон и Готфрид Вильгельм Лейбниц. Это привело к спору за приоритет открытия. Ньютон сформулировал метод флюксий, то есть производных, и флюент (переменных). Лейбниц предложил дифференциальное и интегральное исчисление и ввел символику, которая используется и сейчас, — знаки для дифференциала, интеграла, производной.
Математический анализ развивали многие ученые. Огюстен Луи Коши в начале 19 века создал теорию пределов. За следующие 150 лет появились теории множеств, меры и функций действительного переменного. Работа в этом направлении продолжается до сих пор.
Основные понятия матанализа
Рассмотрим основные термины математического анализа.
Функция
В матанализе функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует только один элемент другого. В свою очередь, множество — это набор математических объектов, например чисел.
Рассмотрим на примере:
\(y=f(x)\)
Здесь одна переменная, где множеству x (области определения функции) сопоставляется множество y (область значений функции). Функцию в математике можно задать как таблицу, график, формулу или правило. В математическом анализе она обычно принимает вид формулы.
Последовательность
Этот объект матанализа похож на функцию. Последовательность — это пронумерованная совокупность объектов, в которой важен их порядок. Однако в ней допускаются повторения. Если мы говорим о числовой последовательности, то объектами будут числа.
Рассмотрим на примере:
\( f : n \rightarrow x \)
n — это натуральные числа, а x — их последовательность. Можно сказать, что последовательность — это та же самая функция, но аргумент здесь — натуральное число.
Ряд
Ряд в математическом анализе — это сумма элементов последовательности. Чтобы получить такой ряд, нужно сложить каждый элемент с предыдущими. Даже если последовательность бесконечная, можно продолжать складывать ее элементы один за другим.
Результат такого процесса зависит от самой последовательности. Если элементы последовательности постоянно увеличиваются, сумма ряда будет стремиться к бесконечности — такой ряд называют расходящимся. Если же сумма ряда приближается к конкретному числу, его называют сходящимся.
Предел
Предел — понятие, с помощью которого определяют состояние функции рядом с конкретной точкой. Изначально его понимали как предельный переход, но позже ученые разделили пределы последовательностей и функций.
Предел последовательности — это число, к которому она стремится по мере увеличения номеров членов до бесконечности. Предел функции описывает поведение функции, когда ее аргументы приближаются к определенному значению.
В математическом анализе пределы важны для изучения непрерывности, интегрирования и дифференцирования.
Производные
Производная — параметр, отображающий, как меняется функция между двумя точками. Визуально она выглядит как касательная к функции: соприкасается с одной точкой и следует параллельно росту функции. Производная помогает измерять скорость изменения функции, выявлять точки перегиба, а также минимальные и максимальные значения на заданном множестве.
Чтобы вычислить производную, нужен предел, потому что функция меняется даже при небольшом приращении.
Для этого используется формула:
\( f′(x) = \lim_{h \rightarrow 0} \frac{f(x + h) — f(x)}{h} \)
где:
— \( f'(x) \) — производная функции \( f(x) \) в точке \( x \), характеризующая скорость изменения функции в этой точке.
— \( \lim_{h \rightarrow 0} \) — предел при \( h \), стремящемся к нулю, то есть мы рассматриваем очень малые изменения \( h \).
— \( f(x + h) \) — значение функции \( f(x) \) в точке \( x + h \), где \( h \) — малое приращение аргумента.
— \( f(x) \) — значение функции в точке \( x \).
— \( h \) — малое изменение аргумента \( x \), на которое сдвигается аргумент функции.
— \( \frac{f(x + h) — f(x)}{h} \) — отношение приращения функции к приращению аргумента, которое приближает производную при достаточно малом \( h \).
В частности, формула полезна при вычислении физических процессов.
Дифференциальные и интегральные уравнения
В математическом анализе дифференциал — это линейное приближение изменения функции в ответ на малое приращение аргумента. Дифференциальным называется уравнение, которое связывает независимую переменную x, неизвестную функцию y(x) и ее производные до заданного предела n.
Оно выглядит так:
\( F(x, y, y′, y′′, \dots, y^n) = 0 \)
Дифференциальные уравнения используются в разных сферах. Например, в химии — для моделирования реакций, в экономике — для прогнозирования изменения спроса.
Интегральные уравнения включают интеграл — сумму бесконечно малых элементов функции. С ее помощью можно решить разные типы задач, например узнать площадь на участке графика. Еще интеграл позволяет рассчитать первообразную: так называется функция, производная от которой совпадает с исходной функцией.
В матанализе выделяют два типа интегралов: определенный, вычисляемый на заданном интервале, и неопределенный, который возвращает функцию с неопределенной константой.
Причины изучать математический анализ
Математический анализ — это основа для многих научных и технических дисциплин. Специалистам в таких областях, как программирование, физика, экономика, инженерия и анализ данных, необходимо владеть его методами для решения профессиональных задач.
Вот несколько примеров, где и для чего используется матанализ:
- Программирование — разработка алгоритмов. Матанализ помогает улучшать алгоритмы, оценивать их сложность и повышать эффективность программ. Расскажем об этом подробнее в следующем разделе.
- Финансы — прогнозирование экономики. С помощью матанализа можно предсказывать изменения на рынках, рассчитывать риски и оптимизировать инвестиции. Он помогает оценивать динамику активов и строить долгосрочные прогнозы.
- Инженерия — моделирование систем. Математический анализ используется для предсказания поведения сложных систем. Например, при проектировании аэрокосмических объектов расчет нагрузок и динамики основан на дифференциальных уравнениях.
- Здравоохранение — анализ данных. В медицине матанализ помогает обрабатывать большие данные для диагностики и разработки новых методов лечения. В биоинформатике его используют для анализа генетики и создания лекарств.
Математический анализ не только помогает решать задачи, но и развивает мышление. Он учит мыслить последовательно, находить оригинальные подходы, улучшает внимание, память и развивает логику.
Применение математического анализа в IT
Математический анализ — основа многих процессов в IT. Он помогает разрабатывать алгоритмы, оптимизировать работу программ, анализировать данные и решать сложные инженерные задачи.
Рассмотрим несколько направлений, где полезен матанализ.
Программирование
Какие задачи поможет решить матанализ:
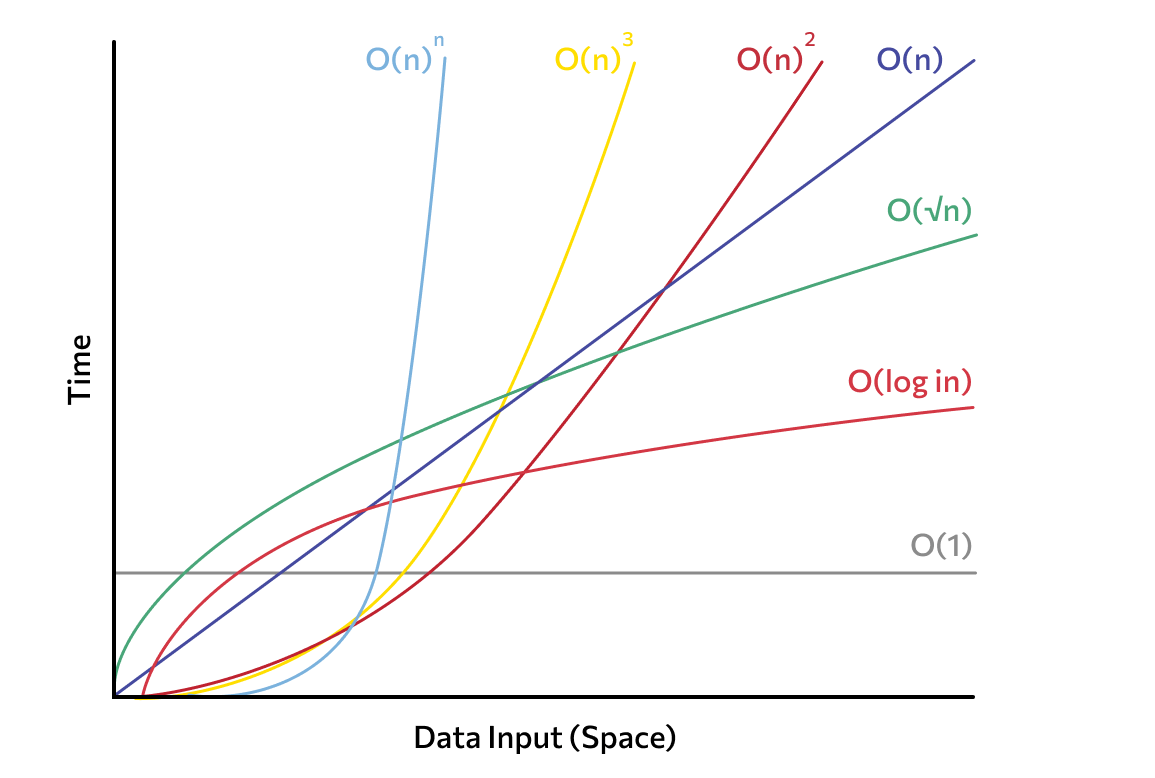
- Рассчитать время выполнения алгоритма. С помощью матанализа можно точно оценить, сколько времени займет выполнение алгоритма в зависимости от его сложности и объема входных данных. А также сравнить несколько алгоритмов и понять, какой из них работает быстрее. Это важно для оптимизации кода и выбора лучшего подхода к решению задачи.
- Улучшить алгоритм. Математический анализ помогает понять, на каких этапах алгоритм замедляется и что можно сделать для его ускорения. Это включает уменьшение количества операций, изменение порядка вычислений или улучшение работы с памятью. Такой подход позволяет находить моменты пиковых нагрузок программы и настраивать работу для более эффективного использования ресурсов, например снижая время простоя процессора или применяя более быстрые структуры данных.
- Создать адаптивный алгоритм. С помощью матанализа можно создать алгоритмы, которые умеют автоматически подстраиваться под текущие условия. Они меняют количество потоков или выбирают более эффективные структуры в зависимости от объема данных или нагрузки на систему. Это полезно, когда ресурсы ограничены или нужно быстро реагировать на изменения условий.
Машинное обучение
Задачи, в которых не обойтись без матанализа:
- Оптимизация моделей. ML-модели постоянно настраиваются для повышения точности предсказаний. С помощью математического анализа можно использовать методы, такие как градиентный спуск, который корректирует параметры модели для уменьшения ошибки.
- Оценка градиентов. При обучении нейронных сетей важно оценивать, как изменение каждого веса влияет на общую ошибку модели. Матанализ помогает вычислить эти градиенты и находить оптимальные значения весов. Это влияет на точность результатов в сложных задачах, таких как распознавание изображений или прогнозирование.
- Разработка моделей. Для описания сложных динамических процессов, которые меняются во времени, часто используют дифференциальные уравнения. С их помощью можно предсказывать траектории в робототехнике, улучшать обработку изображений, прогнозировать климатические явления, анализировать финансовые рынки и т. д. Математический анализ помогает решать такие уравнения, создавая модели, которые точно описывают поведение систем в будущем.
Анализ данных
В Data Science математический анализ используют для решения задач регрессии, классификации и группировки.
- Регрессия: с помощью производных можно определить, как изменения одной переменной влияют на другую.
- Классификация: производные помогают моделям лучше различать объекты, анализируя, как меняется вероятность их принадлежности к разным категориям.
- Группировка данных: интегралы позволяют суммировать изменения и объединять данные в группы, находя закономерности и анализируя поведение объектов.
Геймдев
В сфере разработки игр математический анализ выполняет такие задачи:
- Моделирование поведения объектов. Например, можно точно определить скорость и траекторию движения персонажей или предметов с учетом силы гравитации, трения и сопротивления воздуха. Также математический анализ помогает моделировать состояние веществ, таких как вода, огонь или дым, чтобы они выглядели естественно.
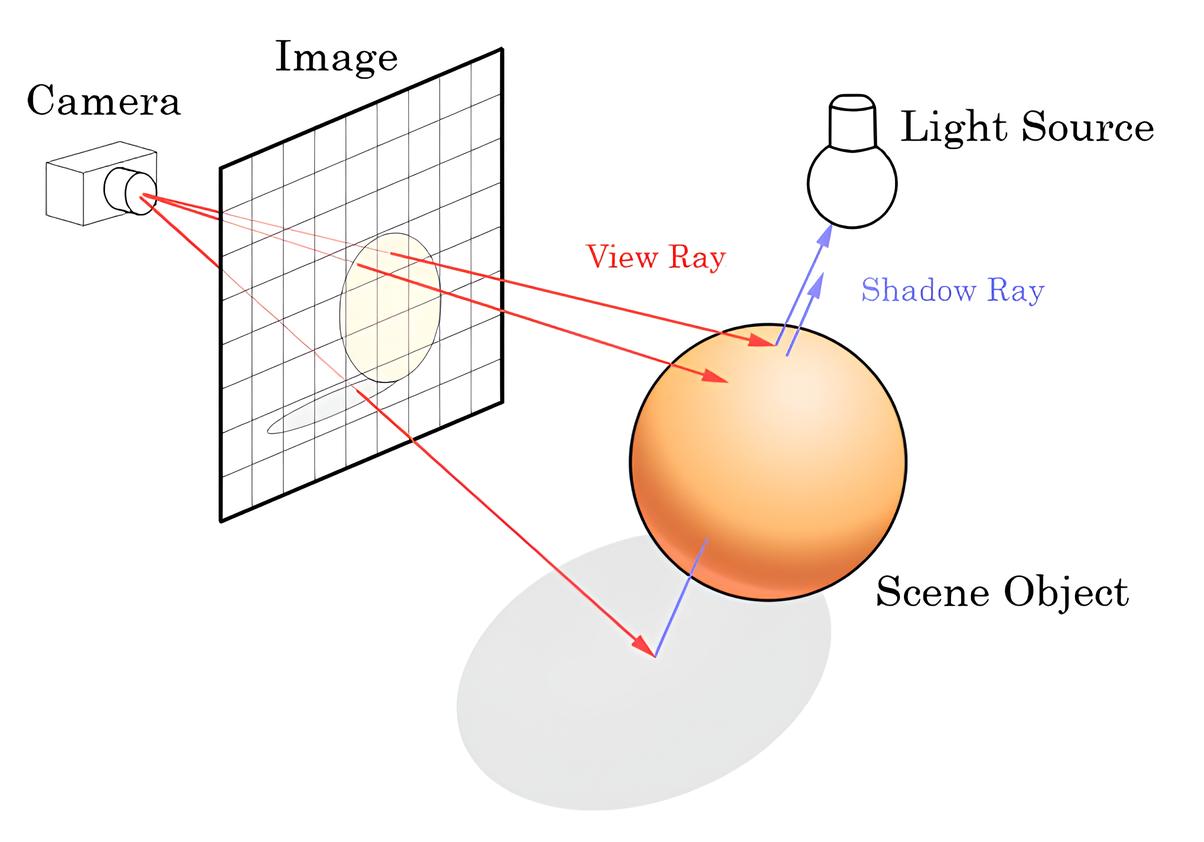
- Реалистичная графика. Для расчета перспективы и проекций геймдизайнеры используют матанализ, чтобы объекты на экране выглядели правильно относительно точки зрения игрока. Кроме того, он нужен для вычисления теней и освещения, чтобы они изменялись в зависимости от угла падения света, положения источников и формы предметов, что делает изображение более правдоподобным.
- Повышение производительности. С помощью матанализа можно выявить узкие места в работе алгоритмов и улучшить их за счет более эффективных вычислений. Это помогает ускорить обработку в реальном времени, особенно в играх с высокой нагрузкой на процессор.
Математический анализ — главное
- Математический анализ помогает разбирать функции на составляющие, изучать их поведение и изменения.
- В математический анализ входят такие понятия, как функция, последовательность, ряд, предел, производная и интеграл.
- Основные разделы матанализа — это интегральное и дифференциальное исчисление. Дифференциальное исчисление изучает производные и скорость изменения функций, а интегральное — суммы бесконечно малых величин и нахождение площадей под кривыми.
- Математический анализ в IT помогает разрабатывать и оптимизировать алгоритмы, анализировать данные, создавать и настраивать модели машинного обучения и проводить вычисления для сложных систем.
- Освоение матанализа не только полезно для решения прикладных задач, но также развивает мышление — учит мыслить последовательно, находить оригинальные подходы, улучшает внимание, память и развивает логику.