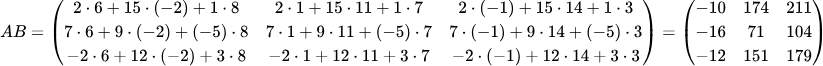В этой статье разбираем важнейшее понятие из высшей алгебры. Поговорим о том, какими бывают матрицы и какие действия можно с ними выполнять. Рассмотрим, как с помощью матриц решать несложные системы линейных уравнений. В конце вы сможете сами решить уравнение и проверить себя.
Что такое матрицы
Любой, кто хоть немного интересовался высшей математикой, слышал это таинственное слово — матрицы. Это важное понятие из области высшей алгебры. Матрица — это прямоугольная таблица элементов. Рассматривать мы будем числовые матрицы, в которых в качестве элементов выступают числа.
Обычно матрицы обозначают прописными латинскими буквами (A, B, C, D…). Рассмотрим такую матрицу:
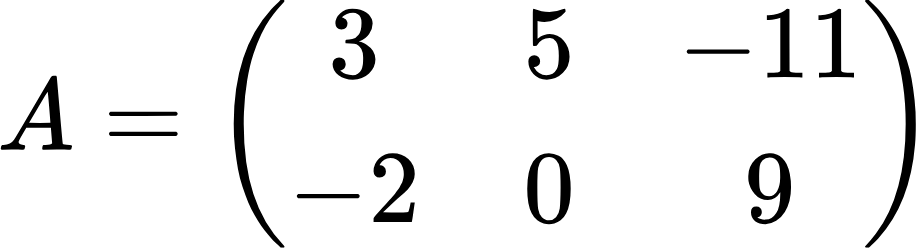
Эта матрица состоит из двух строк и трех столбцов. Всего в состав матрицы входит 6 элементов. Элементы в матрице существуют сами по себе. То есть ни о каких сложениях или вычитаниях речи не идет. Матрица — это просто набор чисел.
Если у матрицы совпадает количество строк и столбцов, то такую матрицу называют квадратной:
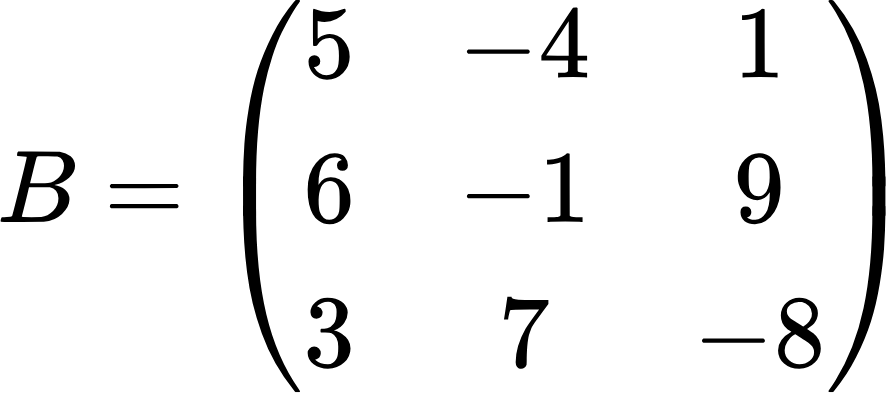
Векторами называют матрицы, у которых одна строка или один столбец. Вот пример вектора:
Это тоже вектор:
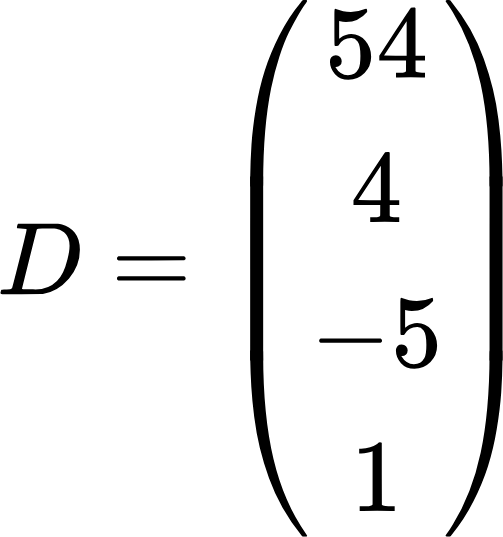
Далее переходим к рассмотрению действий с матрицами.
Вынесение и внесение минуса
Рассмотрим следующую матрицу:
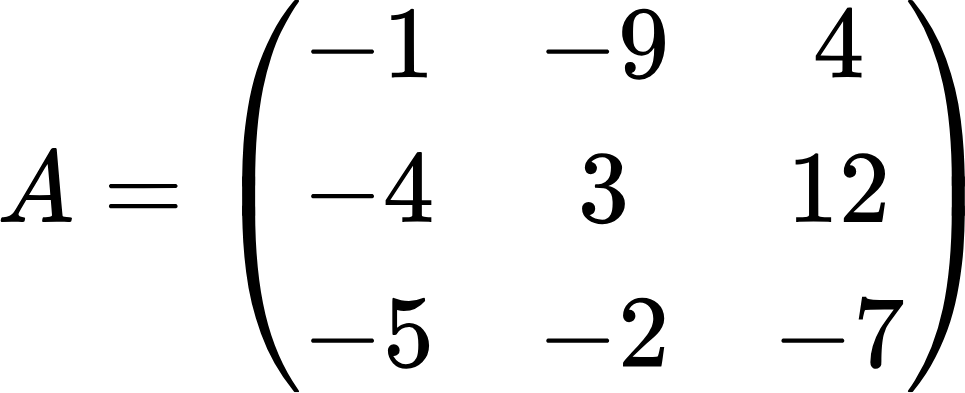
Слишком много отрицательных чисел. Это может быть неудобно при различных операциях с матрицей. Вынесем минус за пределы матрицы. Для этого поменяем у каждого числа знак на противоположный:
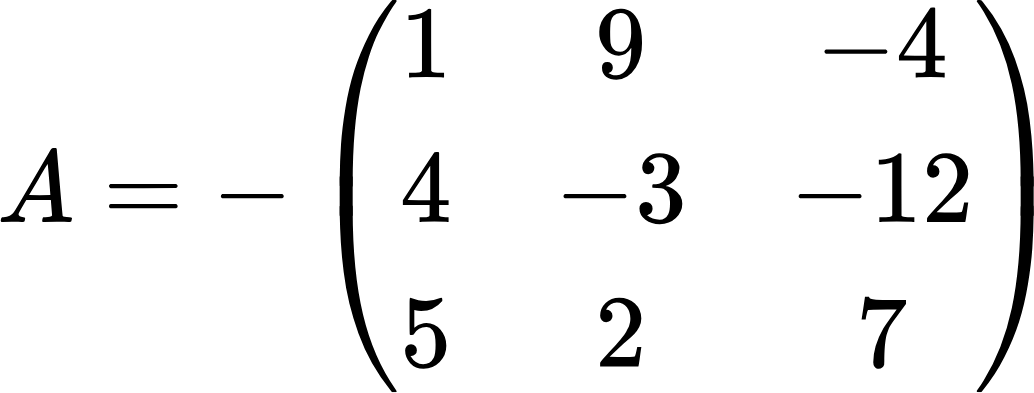
Для обратной операции внесения минуса нужно точно так же поменять все знаки у элементов матрицы на противоположные. В результате получим исходную матрицу.
Умножение матрицы на число
Вспомним правило: чтобы умножить одночлен на многочлен, надо каждый член многочлена умножить на этот одночлен и полученные произведения сложить. С умножением матрицы на число дело обстоит примерно так же: чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на это число. Например, умножим матрицу
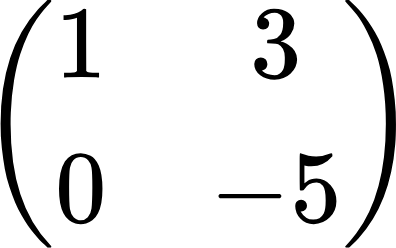
на 2. Получим:
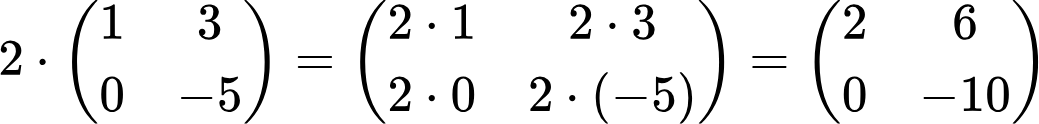
Транспонирование матриц
Чтобы транспонировать матрицу, нужно ее строки записать в виде столбцов. Самый простой пример транспонирования получается с векторами. Возьмем такой вектор:

И просто превратим строку в столбец:
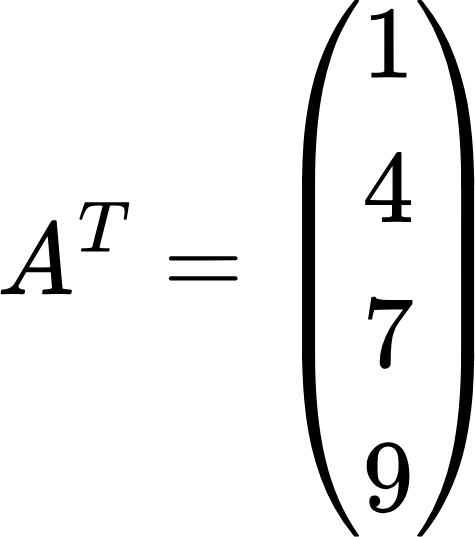
Транспонированные матрицы обычно обозначаются надстрочным индексом T, расположенным сверху и справа от буквы, или же можно использовать штрих вместо индекса. Теперь давайте транспонируем матрицу посложнее:
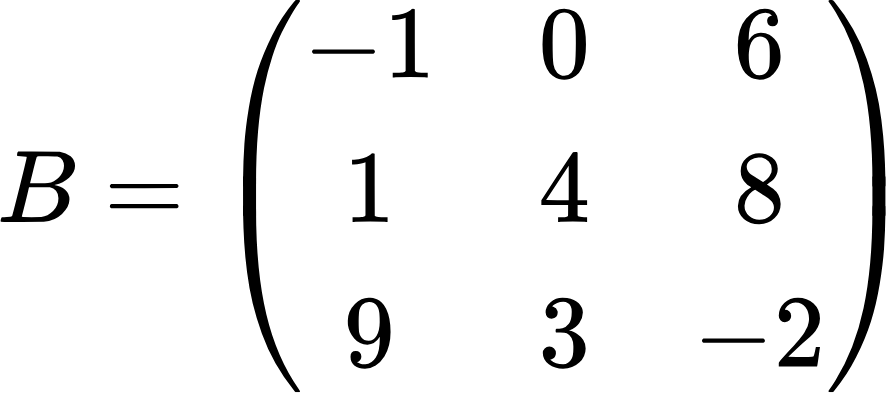
Сначала переписываем первую строку (самую верхнюю) в первый столбец:
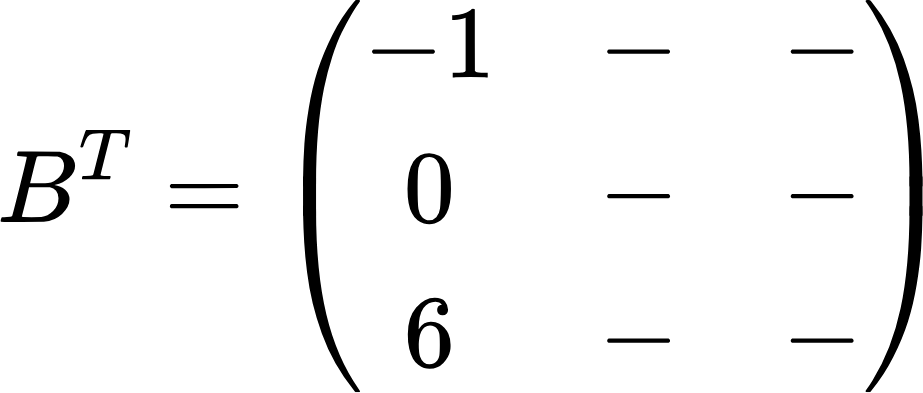
Дальше переписываем вторую строку во второй столбец:
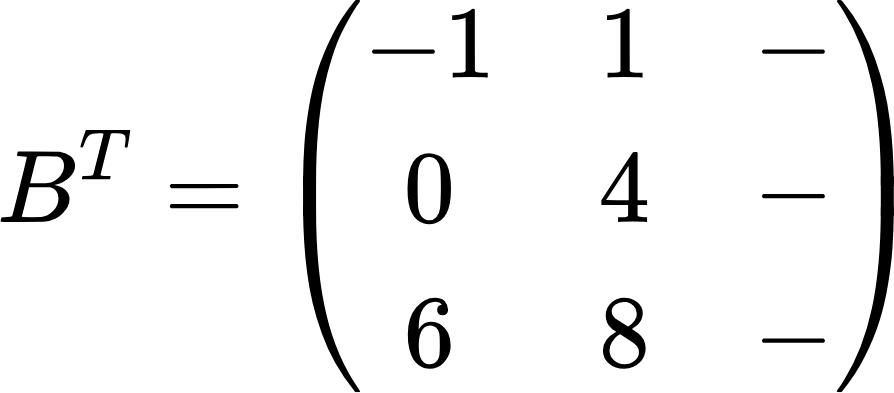
И, наконец, осталось только переписать последнюю строку в последний оставшийся столбец:
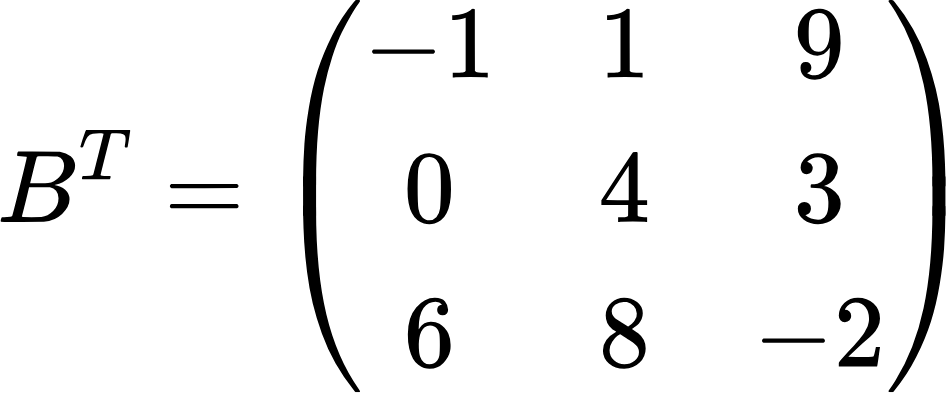
Получили транспонированную матрицу.
Сумма и разность матриц
Для того чтобы сложить матрицы, нужно сложить их соответствующие элементы. Чтобы найти разность матриц, надо найти разность их соответствующих элементов.
Не все матрицы можно складывать или вычитать. Для операций сложения или вычитания нужно, чтобы матрицы были одинаковыми по размеру. То есть если, например, нам дана матрица три на три (третьего порядка), то ее можно складывать только с такой же по размеру матрицей и ни с какой другой.
Теперь рассмотрим, как складывать матрицы на конкретном примере. Сложим матрицы:
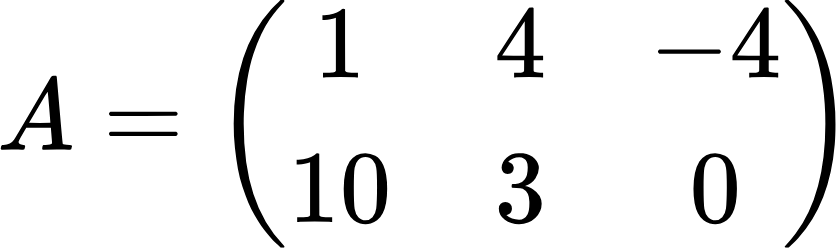
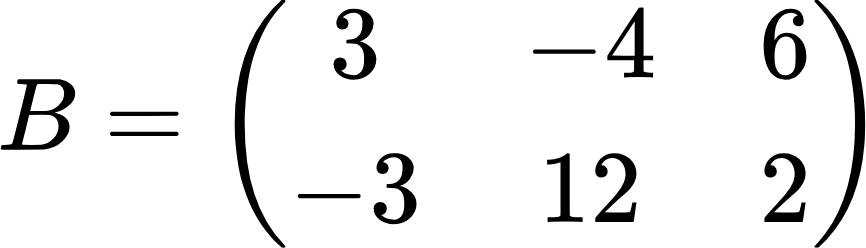
Слаживаем соответствующие элементы матриц:
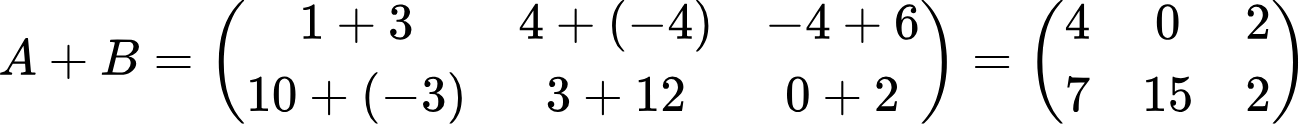
Найдем разность следующих матриц:
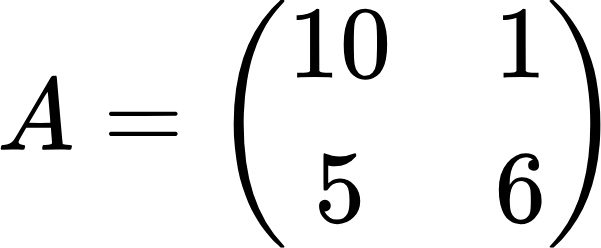
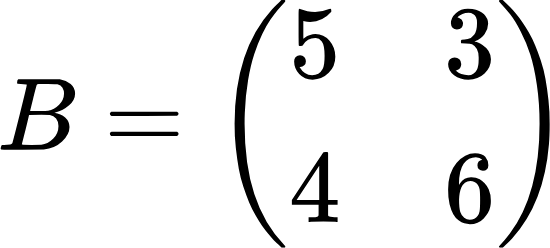
Находим разность соответствующих элементов матриц:
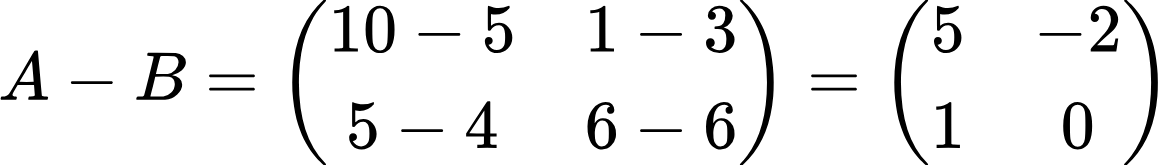
Строго говоря, вычитание — это то же самое сложение, только вычитаемое становится слагаемым и берется с противоположным знаком. Например, вместо того, чтобы отнимать от 1 число 3, мы можем прибавить к 1 число −3 или, наоборот, к −3 прибавить 1, так как от перестановки слагаемых сумма не меняется:
1-3=1+(-3)=-3+1=-2
Это ярко проявляется в многочленах. Многочлен — это сумма одночленов, просто одночлены идут с разными знаками.
Умножение матриц
Не все матрицы можно перемножать. Чтобы матрицу A можно было умножить на матрицу B, необходимо, чтобы число столбцов матрицы A равнялось числу строк матрицы B.
Разберем на конкретных примерах. Сначала мы приведем формулу, а потом по ней перемножим парочку матриц. Первая формула для самого простого случая:
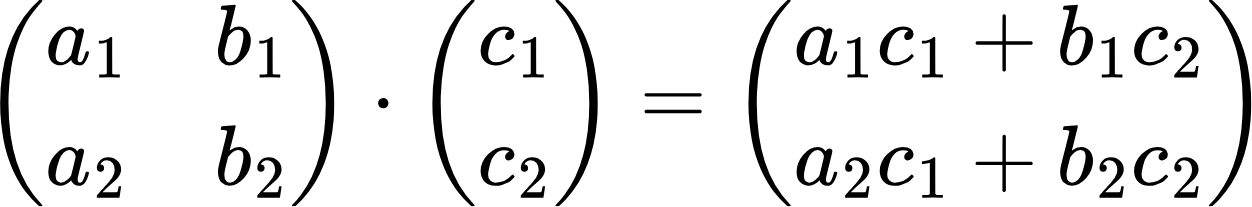
Перемножим по ней эти две матрицы:
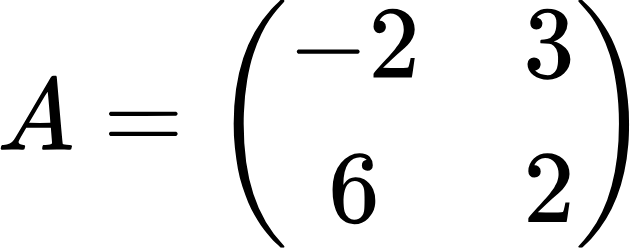
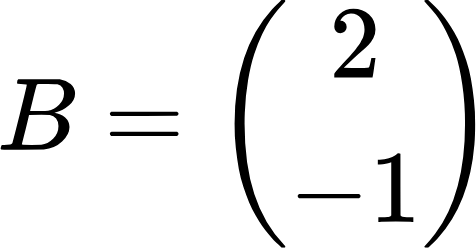
Как видно из формулы, чтобы получить произведение этих матриц, нужно каждый элемент верхней строки первой матрицы умножить на соответствующий элемент второй матрицы и получившиеся произведения сложить. Таким образом получаем первый элемент произведения. Также поступаем с нижней строкой первой матрицы и в результате получаем второй элемент произведения. По сути, при умножении матриц применяется принцип «строка на столбец»:
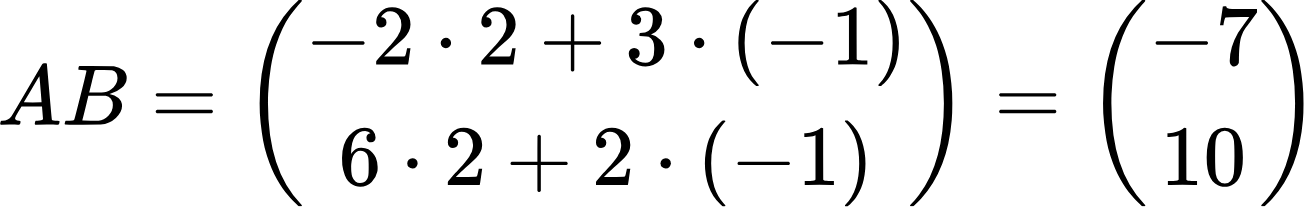
Теперь рассмотрим пример посложнее. Формула:
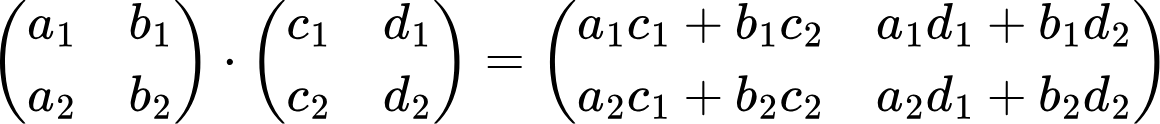
Найдем произведение следующих матриц:
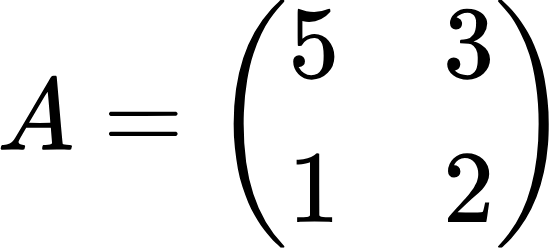
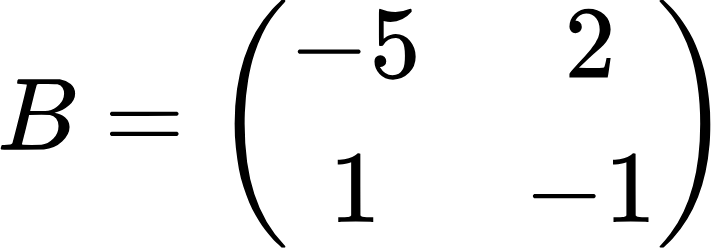
Чтобы получить первый столбец произведения, перемножаем и складываем элементы первой матрицы и элементы первого столбца второй матрицы. Чтобы получить второй столбец произведения, перемножаем и складываем элементы первой матрицы и элементы второго столбца второй матрицы. Здесь также для получения любого элемента произведения применяется принцип «строка на столбец». Применяем формулу:
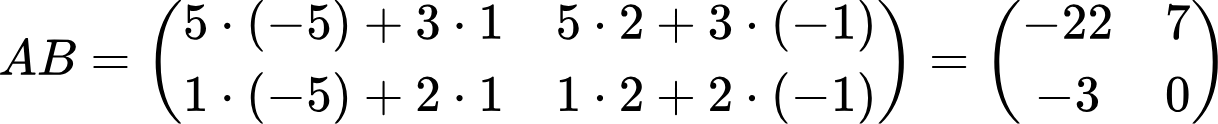
Аналогично умножаются матрицы и более внушительных размеров, только формулы для элементов произведения там будут подлиннее. Пример:
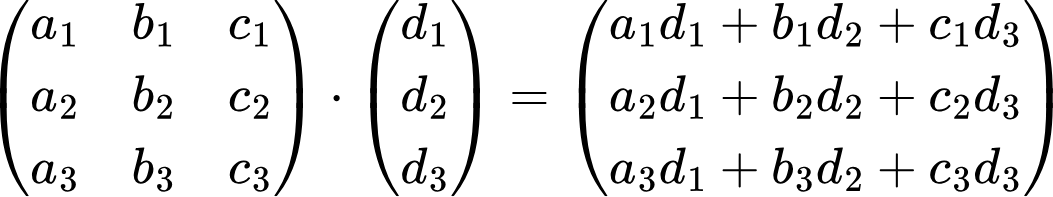
Как видно, здесь у каждого элемента произведения по три слагаемых. Пример применения этой формулы:
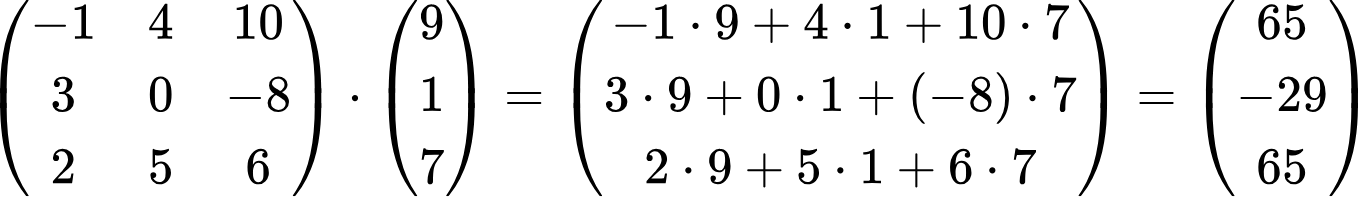
Вычисление определителей
Определители нужны, например, чтобы находить обратные матрицы и решать системы линейных уравнений. Допустим, нам дана матрица:
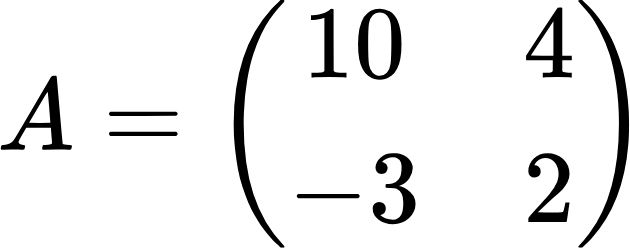
Ее определитель обозначается как A, но также довольно часто можно встретить обозначение определителя латинской буквой D или греческой . Вычисление или нахождение определителя также называют раскрытием определителя. Раскрыть определитель — это значит найти некоторое число. Определитель можно вычислить только для квадратной матрицы. Самый простой определитель — это определитель два на два (второго порядка). Его можно вычислить по следующей формуле:
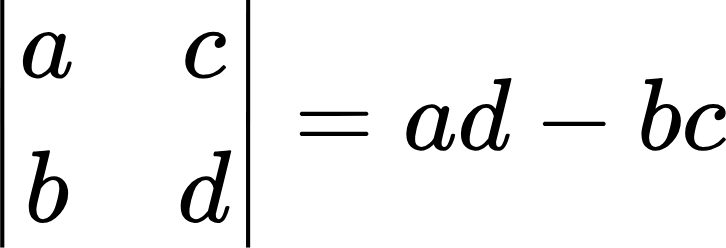
Найдем, например, определитель для вышеприведенной матрицы A:
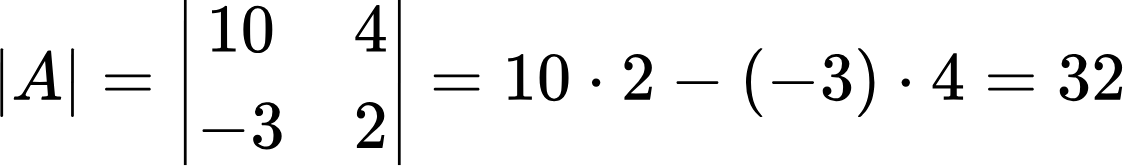
Теперь рассмотрим более сложный случай. Допустим, дана следующая матрица:
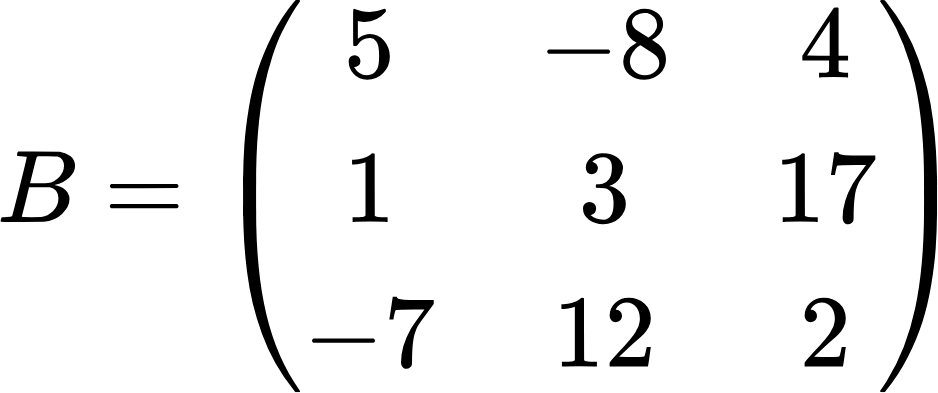
Требуется раскрыть ее определитель. Делается это по такой формуле:
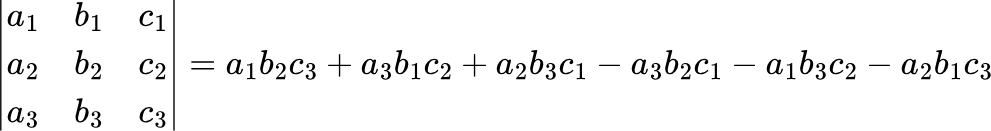
Применяем формулу к матрице B:
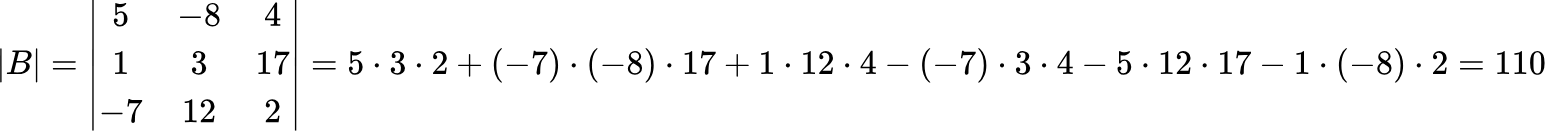
Переходим к следующему действию.
Нахождение обратной матрицы
Как и в случае определителей, обратную матрицу можно найти только для квадратной матрицы. Еще и не для всякой квадратной матрицы существует ей обратная, а только для такой, у которой определитель не равен нулю. Обратные матрицы обозначаются как A-1 и вычисляются по следующей формуле:
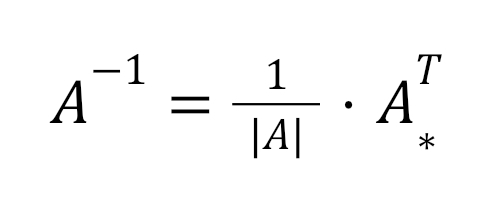
Где |A| — определитель матрицы, а A*T — транспонированная матрица алгебраических дополнений соответствующих элементов матрицы A.
В качестве примера найдем обратную матрицу для следующей матрицы:
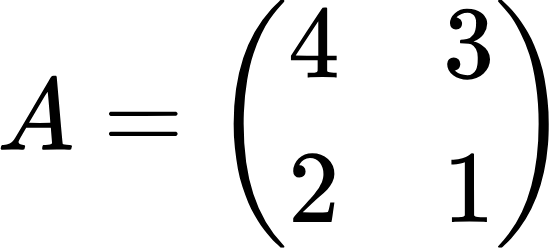
Сначала найдем определитель:
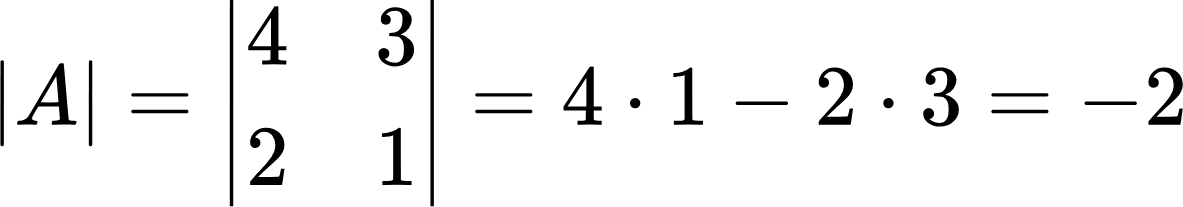
Определитель не равен нулю, а значит обратная матрица существует. Далее нам понадобится так называемая матрица миноров. Она имеет такие же размеры, как и исходная матрица:
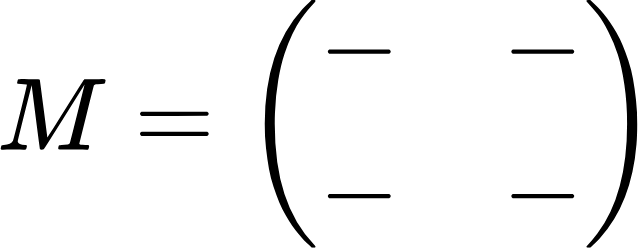
Нам надо ее заполнить. Как это сделать? Обратимся к исходной матрице и возьмем первый ее элемент (число 4), потом мысленно вычеркнем строку и столбец, в которых он находится. Оставшееся число (1) и будет искомым минором. Записываем его как первый элемент матрицы миноров:
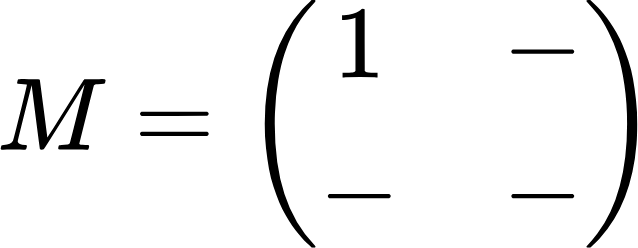
Теперь берем второй элемент исходной матрицы (число 3) и также вычеркиваем его строку и столбец. Остается число 2, которое заносим в нашу матрицу миноров:
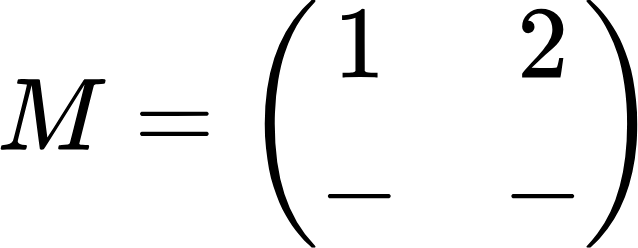
Такую же операцию проделываем и с оставшимися элементами. Сначала с двойкой, а потом с единицей. В результате матрица миноров должна иметь следующий вид:
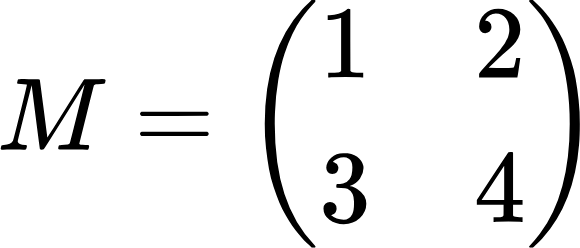
А дальше превращаем матрицу миноров в матрицу алгебраических дополнений. Для этого просто меняем знаки на противоположные у второго и третьего элемента матрицы миноров, то есть у чисел 2 и 3. В результате получим:
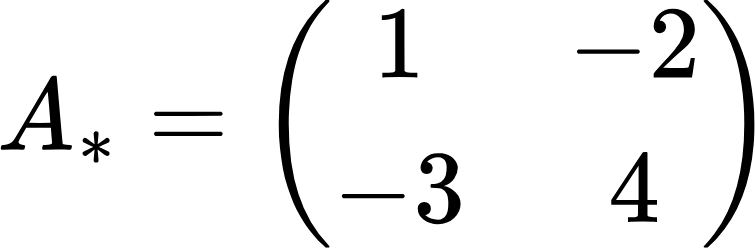
Транспонируем эту матрицу и получаем:
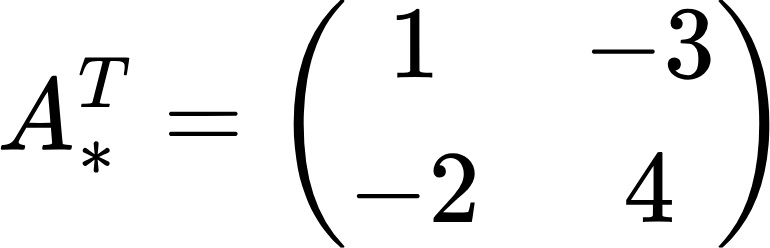
Согласно приведенной в начале этого раздела формуле, обратная матрица будет иметь следующий вид:
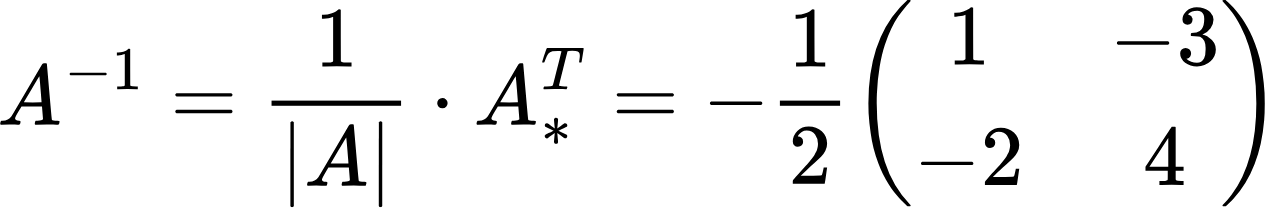
Умножив транспонированную матрицу алгебраических дополнений A*T на -12, получим:
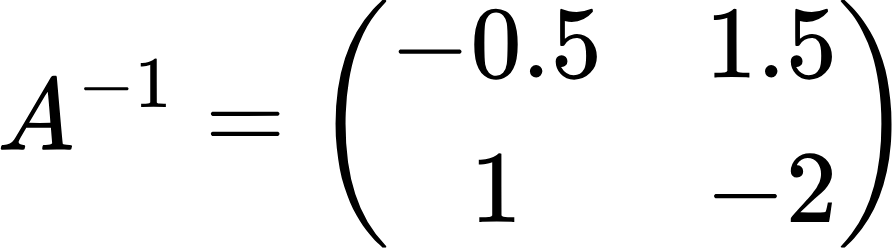
Как проверить, что мы правильно нашли обратную матрицу? Здесь можно провести аналогию с обычными числами, где при умножении какого-либо числа на ему обратное число получается единица:
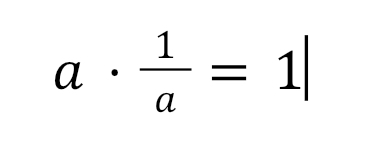
То есть, если умножить исходную матрицу на обратную, тоже должно получится что-то подобное единице. Так и есть. В результате должна получиться так называемая единичная матрица:
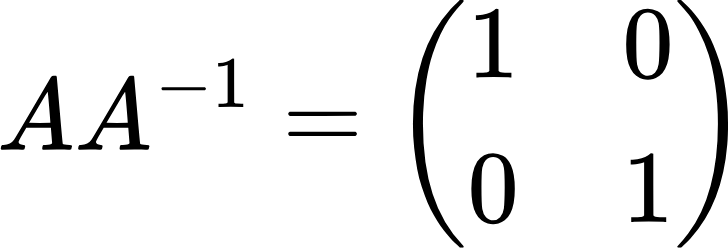
Сделаем проверку:
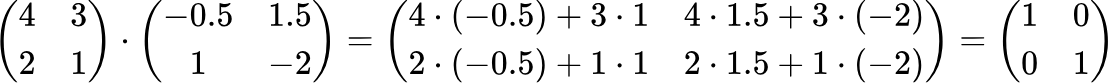
Получили единичную матрицу, а это значит, что обратная матрица найдена верно.
Решение систем уравнений с помощью формул Крамера
Разберем, как при помощи матриц, а вернее их определителей, решать системы линейных уравнений с двумя переменными. Делать это мы будем по формулам Крамера. Итак, пусть нам дана такая система уравнений:
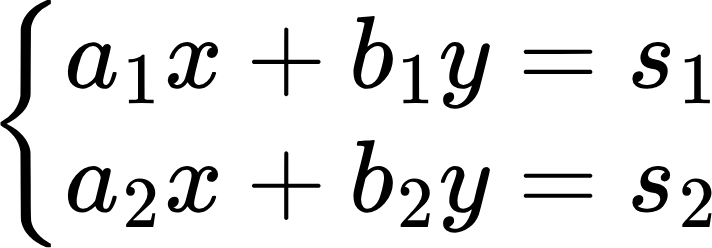
Чтобы ее решить, для начала надо вычислить главный определитель системы:
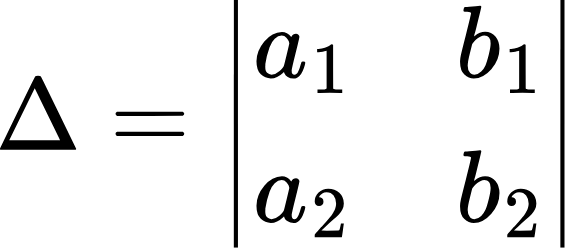
Если =0, то решений системы бесконечное множество или же их нет вовсе, а если 0, то система имеет одно-единственное решение. Далее нужно найти два вот таких определителя:
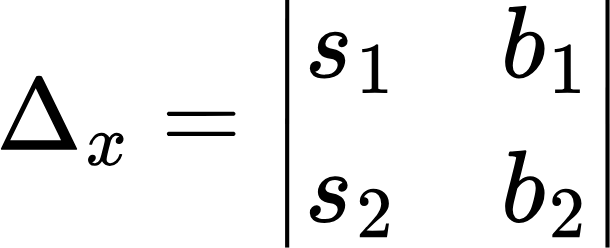
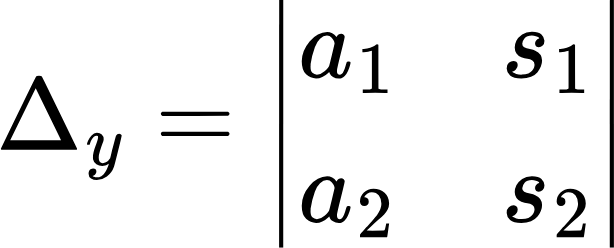
После того как все определители найдены, можно вычислять корни системы по следующим формулам:
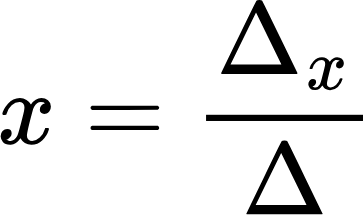
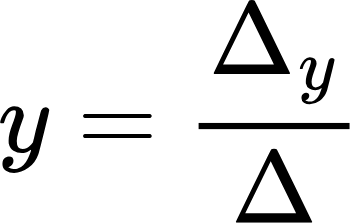
В качестве примера давайте решим систему уравнений:
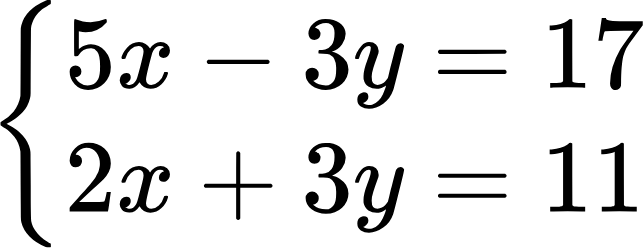
Ищем главный определитель:
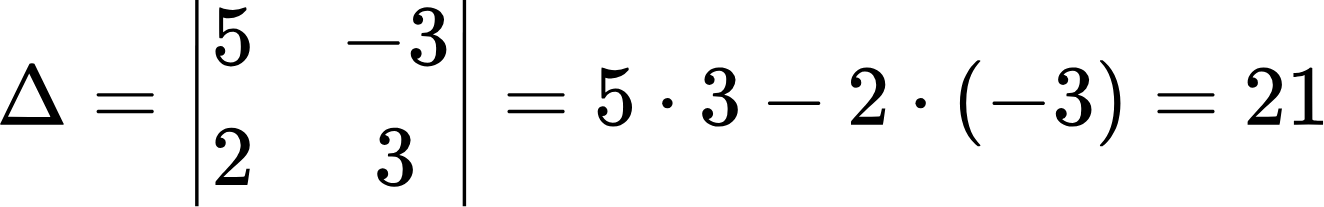
Главный определитель не равен нулю, значит система имеет одно решение. Вычисляем остальные определители:
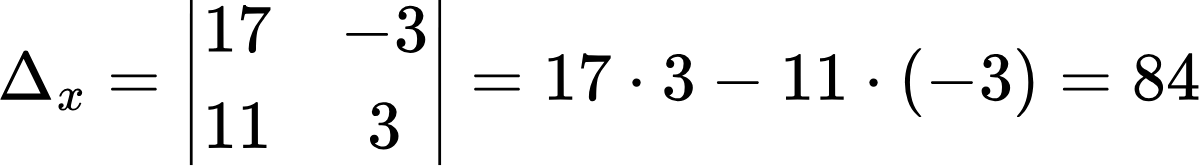
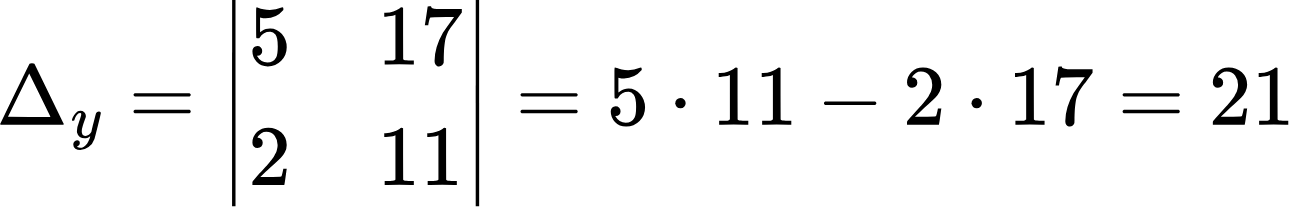
Все определители найдены, и теперь можно заняться вычислением корней:
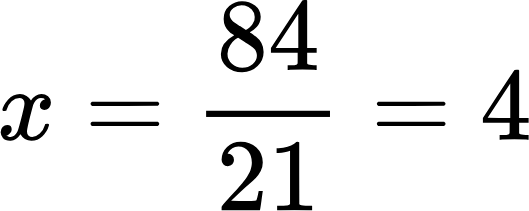
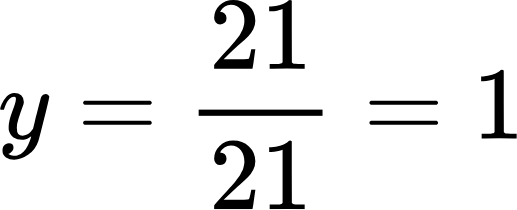
Сделаем проверку, подставив найденные корни в систему:
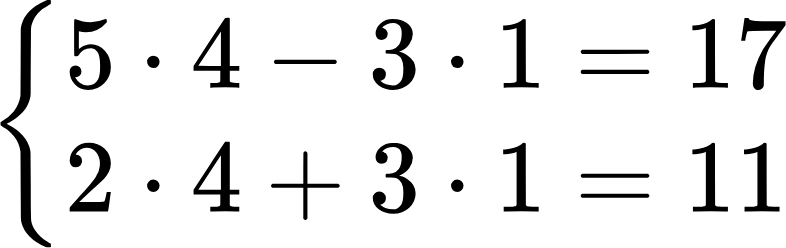
Получили два верных числовых равенства, а это значит, что система уравнений решена верно.
Приведем еще один пример. Решим систему:
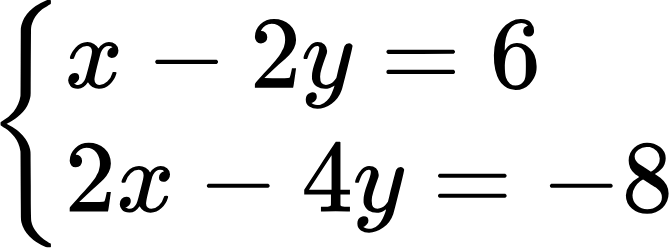
Ищем главный определитель:
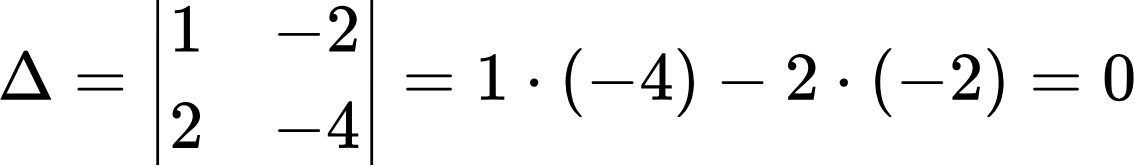
Как видим, определитель равен нулю, а значит, система может иметь бесконечное множество решений или не иметь их вообще. Уточним это с помощью способа подстановки. Выразим из первого уравнения x через y:
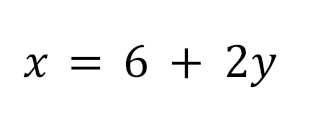
Подставим правую часть этого выражения вместо x во второе уравнение:
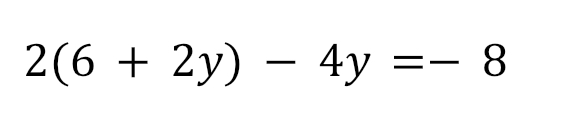
Делаем необходимые преобразования:
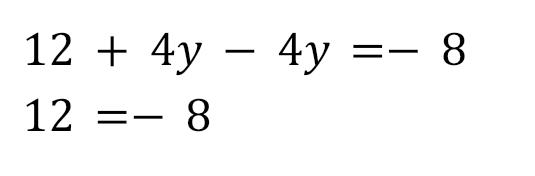
Получили неверное числовое равенство, а значит, система не имеет решений.
Решим еще одну систему:
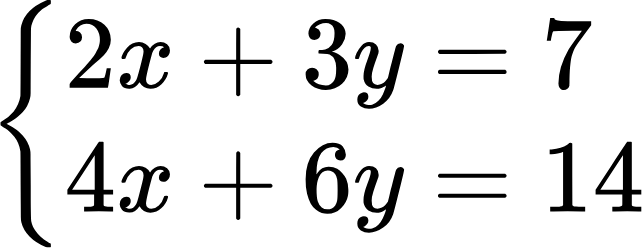
Главный определитель этой системы тоже равен нулю:
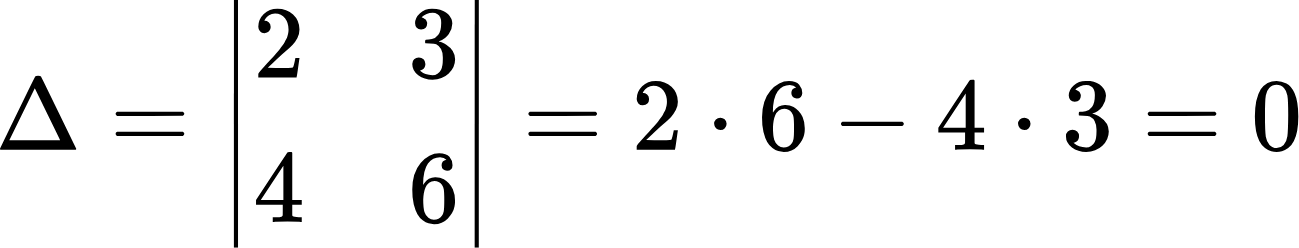
Присмотримся повнимательней к уравнениям системы. Если умножить первое уравнение на 2, то мы получим второе уравнение. Или если разделить второе уравнение на 2, то мы получим первое уравнение. То есть эти уравнения равносильны и по сути мы имеем дело с одним уравнением с двумя неизвестными, а они, как известно, имеют бесконечное множество решений. Значит, и исходная система уравнений имеет бесконечное множество решений.
Задание для самостоятельного выполнения
В разделе про умножение матриц мы рассмотрели примеры умножения матриц второго порядка и умножения матрицы третьего порядка на вектор. Учитывая эти примеры, произведите умножение следующих матриц:
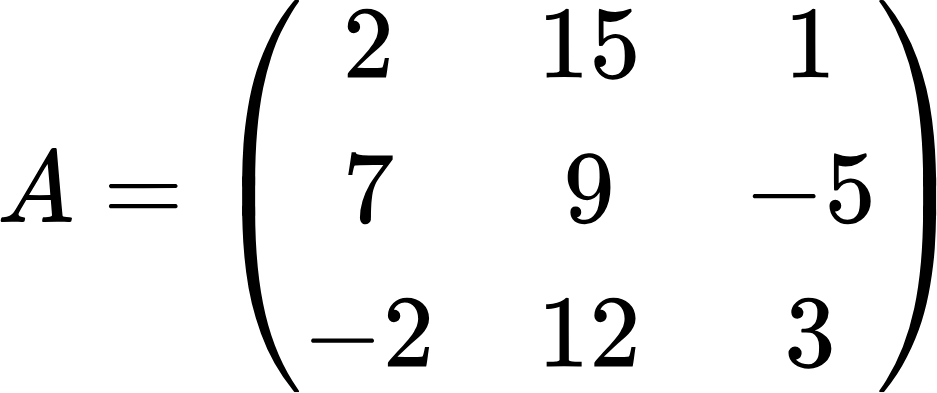
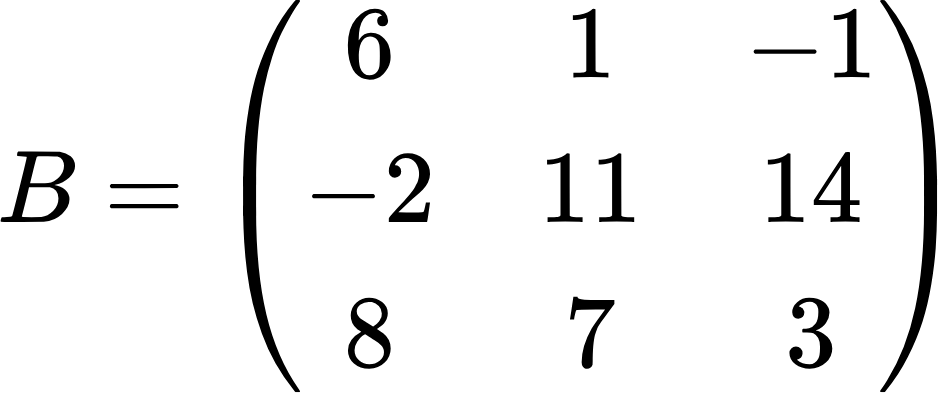
Так как перемножаются матрицы третьего порядка, то в результате тоже должна получиться такая же матрица. Применяя принцип строка на столбец, получим: