Что такое факториал числа и как его считать

Факториал часто встречается в математике, особенно часто — в задачах комбинаторики и математического анализа. Разберемся с факториалом и научимся решать простые задачи.

Что такое факториал

Иногда в математике надо посчитать произведение натуральных чисел, следующих по порядку и начинающихся с единицы. Если стоит задача посчитать произведение до десятка, то такая запись помещается в одну строчку: 1 × 2 × 3 × 4 × 5. Если вычисления доходят до нескольких десятков или даже сотен, то только на запись выражения может уйти достаточно много времени. Для его экономии и более компактного вида в математике существует факториал.

Факториал натурального числа n — это произведение всех натуральных чисел от 1 до n, включая само n. Факториал записывается в виде восклицательного знака после числа (n!), а произносится как «эн факториал». Зная все это, выражение выше можно записать более компактно: 1 × 2 × 3 × 4 × 5 = 5! = 120. Факториал активно применяется в комбинаторике, теории чисел, математическом анализе, функциональном анализе и других разделах математики.

Натуральные числа — это числа, встречающиеся естественным образом во время порядкового счета (1, 2, 3, 4, 5 и далее). Последовательно расположенные натуральные числа в порядке возрастания называют натуральным рядом.

Базовые свойства факториала

Важно запомнить, что в математике факториал может быть только натуральным числом. Поэтому нельзя вычислить факториал отрицательного или дробного числа. Также важно запомнить:

• факториал нуля всегда равен единице — 0! = 1;
• факториал единицы всегда равен единице — 1! = 1.

Для быстрого вычисления можно пользоваться таблицей факториалов, которая содержит уже посчитанные факториалы чисел:

n!	Значение
1!	1
2!	2
3!	6
4!	24
5!	120
6!	720
7!	5 040
8!	40 320
9!	362 880
10!	3 628 800
11!	39 916 800
12!	479 001 600
13!	6 227 020 800
14!	87 178 291 200
15!	1 307 674 368 000
16!	20 922 789 888 000
17!	355 687 428 096 000
18!	6 402 373 705 728 000
19!	121 645 100 408 832 000
20!	2 432 902 008 176 640 000

Из таблицы можно заметить, что факториал — быстрорастущая функция. Значение 10! уже преодолевает разряд тысяч, переходя в миллионы.

Рекуррентная формула факториала

Факториал подвержен рекурсии, что упрощает процесс его вычисления. Рассмотрим на простом примере. Надо найти значение 6!. Для этого разложим компактную запись факториала на отдельные множители: 6! = 1 × 2 × 3 × 4 × 5 × 6. Можно начать перемножать все числа друг за другом, но из записи видно, что можно сэкономить время, умножив факториал пяти на шесть: 5! × 6. Мы уже знаем, что факториал 5 равен 120, поэтому просто умножим значение на шесть и получим 720: 6! = 1 × 2 × 3 × 4 × 5 × 6 = 5! × 6 = 720.

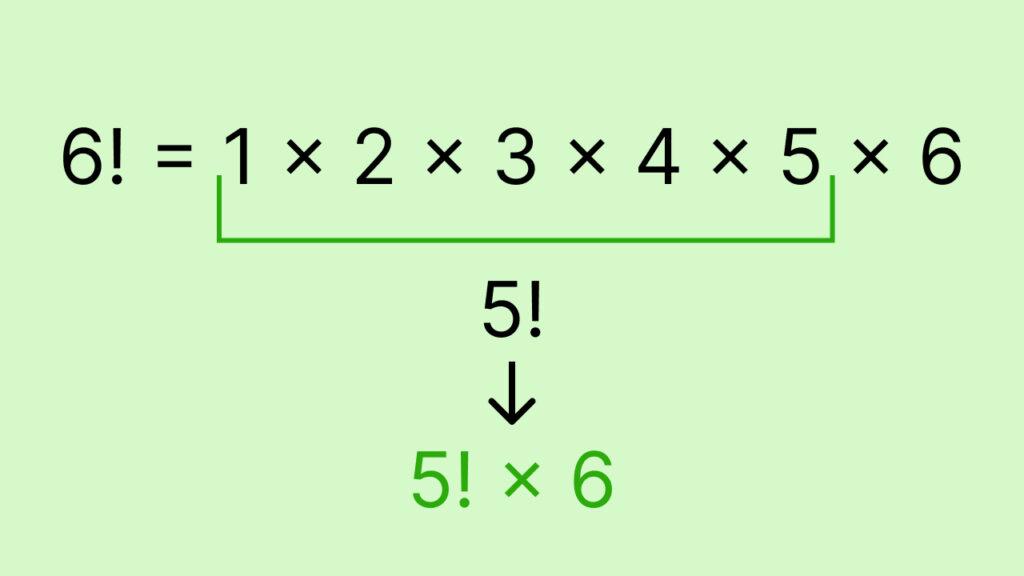
Рекуррентную формулу факториала в общем виде можно записать так:
n! = (n — 1)! × n. Такую формулу удобно использовать для построения алгоритмов вычисления факториала в программировании, но считать с ней факториалы больших чисел долго и сложно. Например, если надо найти 100!, то нужно знать 99!, потому что 100! = 99! × 100.

Воспользуемся рекуррентной формулой факториала для вычисления с помощью Python. Код функции будет выглядеть так:

def factorial(n):
    # Обработка стандартных значений
    if n == 1 or n == 0:
        return 1
    else:
        # Обработка значений больше единицы
        return factorial(n-1) * n

Создаем функцию factorial и передаем в качестве аргумента значение n. Если n равно нулю или единице, то возвращаем единицу согласно базовым свойствам факториала. В остальных случаях рекурсивно вызываем функцию factorial со значением n-1. Попробуем запустить функцию для различных чисел и сравнить результат с таблицей факториалов:

print(factorial(5))
print(factorial(10))
print(factorial(15))
print(factorial(999))

Вывод:
>>> 120
>>> 3628800
>>> 1307674368000
>>> RecursionError: maximum recursion depth exceeded in comparison

Резульатыт работы функции верные, а это значит, что код работает. Можно заметить, что при попытке вычислить 999! программа выдала ошибку. Связано это с максимальной глубиной рекурсии — в Python по умолчанию установлен лимит на 998 рекурсивных вызовов. Глубину рекурсии можно увеличить, если перед функцией указать новое значение лимита:

import sys

sys.setrecursionlimit(2000)

Теперь рекурсивно функцию можно вызывать до 2 тыс. раз, но это может нагружать компьютер, особенно если вычислять большие значения.

Формула Стирлинга

Вычисление факториала числа n путем нахождения произведения всех натуральных чисел от 1 до n может занять много времени. Такие задачи сложно обрабатывать даже с помощью компьютера. Все из-за того, что функция факториала растет слишком быстро. Облегчить задачу можно с помощью формулы шотландского математика Джеймса Стирлинга, которая позволяет быстро вычислить приближенное значение факториала. Общая запись формулы выглядит следующим образом:

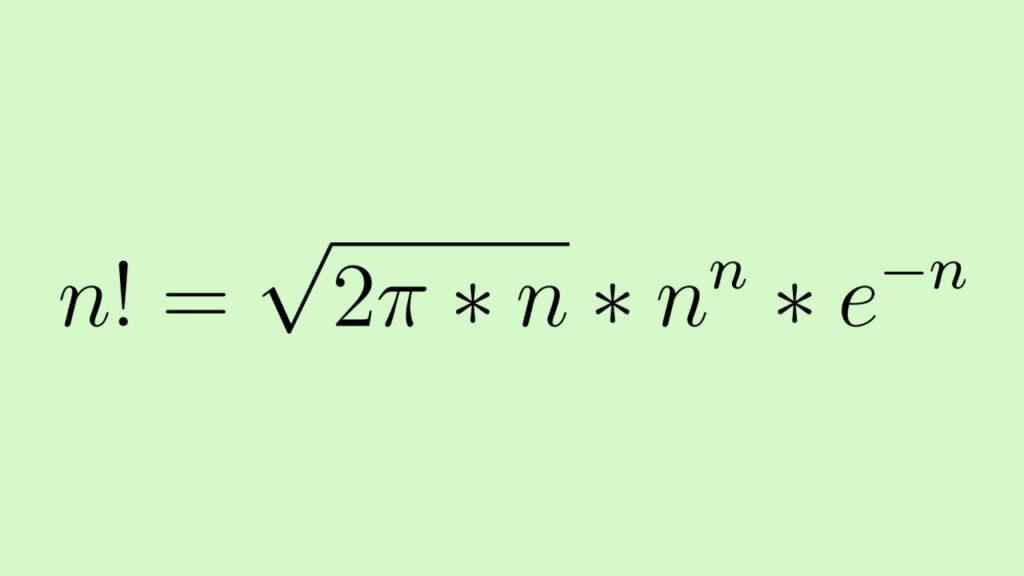
Для понимания формулы напомним, что π приблизительно равно 3,14, а e — 2,71. После этого в формулу Стирлинга останется только подставить значение n и выполнить математические операции.

Рассмотрим пример нахождения 5! с помощью формулы Стирлинга:

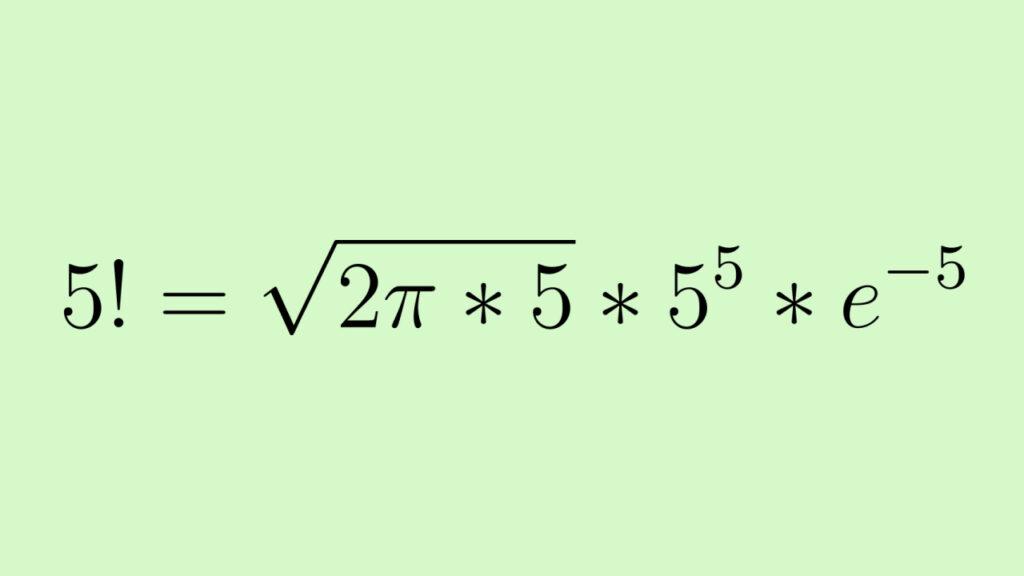
После ряда преобразований и вычислений получим, что 5! = 118,019. Если перемножить числа одно за другим, то 5! = 120. На примере хорошо видно, что значение получается приближенным. Для малых значений n, как в примере выше, погрешность будет больше, чем для больших.

Где применяется факториал

Наглядная область применения факториала — задачи на перестановки без повторений из комбинаторики. Рассмотрим на примере.

Задача

На банкет пригласили группу, состоящую из 6 человек. Сколькими способами можно разместить гостей за одним столом?

За столом есть шесть мест, по одному для каждого гостя:

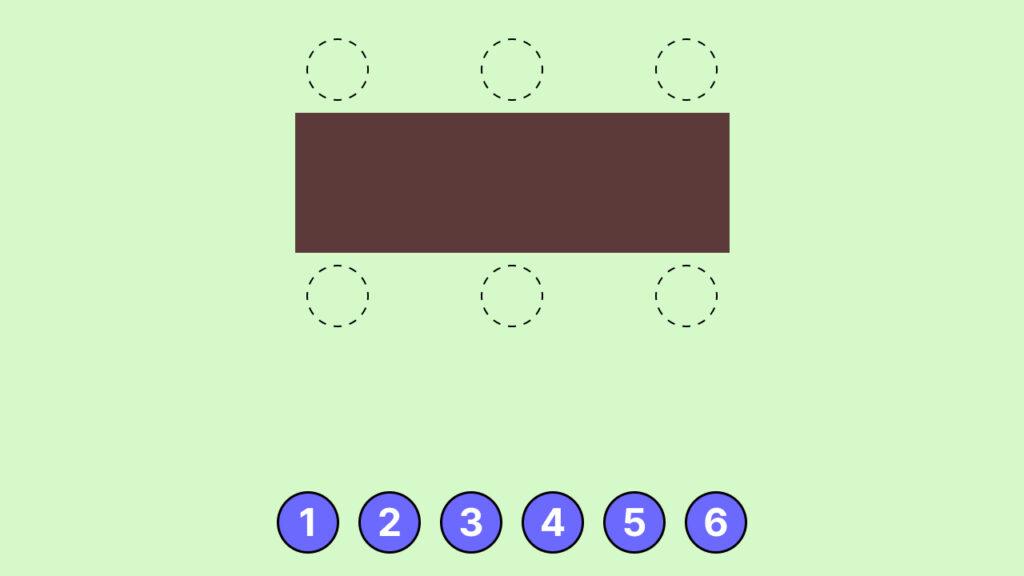
Можно попробовать посчитать вручную все возможные комбинации размещения гостей, но это займёт много времени. Во-первых, уже учтенные комбинации надо запоминать и при каждой новой комбинации проверять, нет ли уже такой. Во-вторых, очень легко упустить возможную комбинацию.

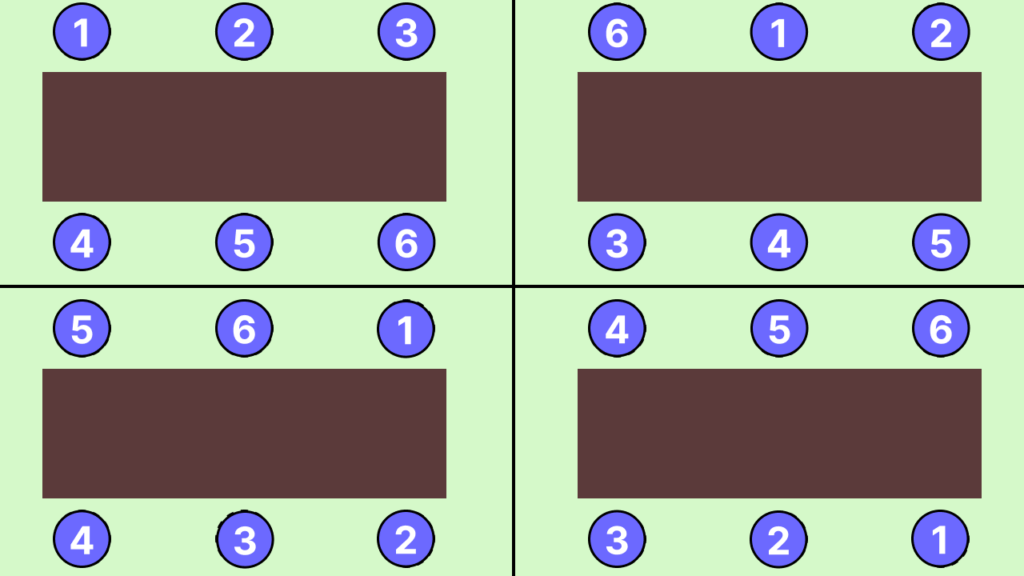
Такие задачи можно легко и быстро решать с помощью факториала. Для этого каждому месту присвоим букву латинского алфавита от A до F:

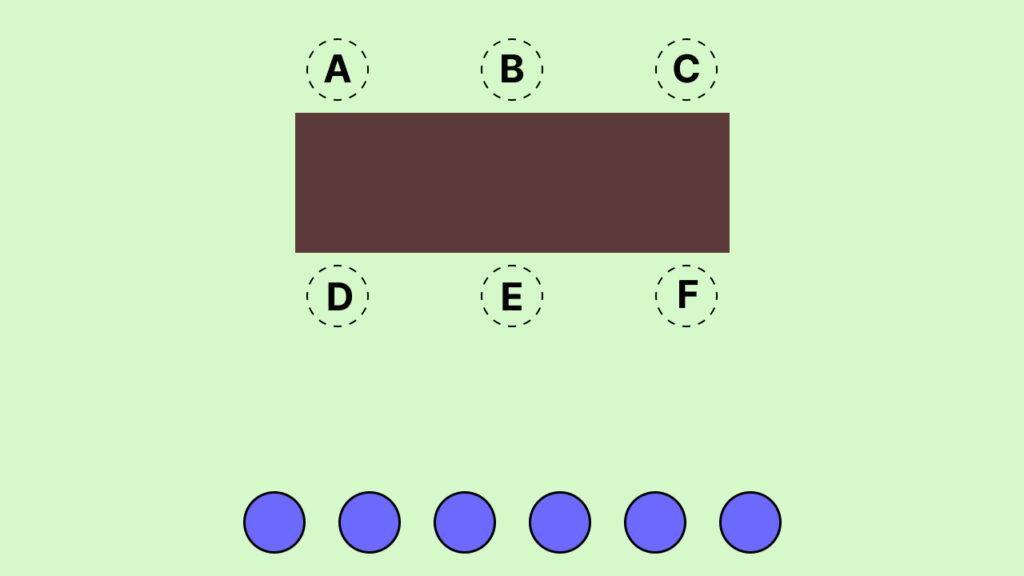
На место под буквой A мы можем расположить любого из 6 гостей, у нас останется еще 5. На место под буквой B уже можно посадить любого из 5 гостей, останется 4. На место под буквой C можно посадить любого из 4 гостей, останется еще 3. И так далее. На последнее место F можно посадить всего одного гостя, так как остальных уже рассадили. Получим следующую ситуацию:

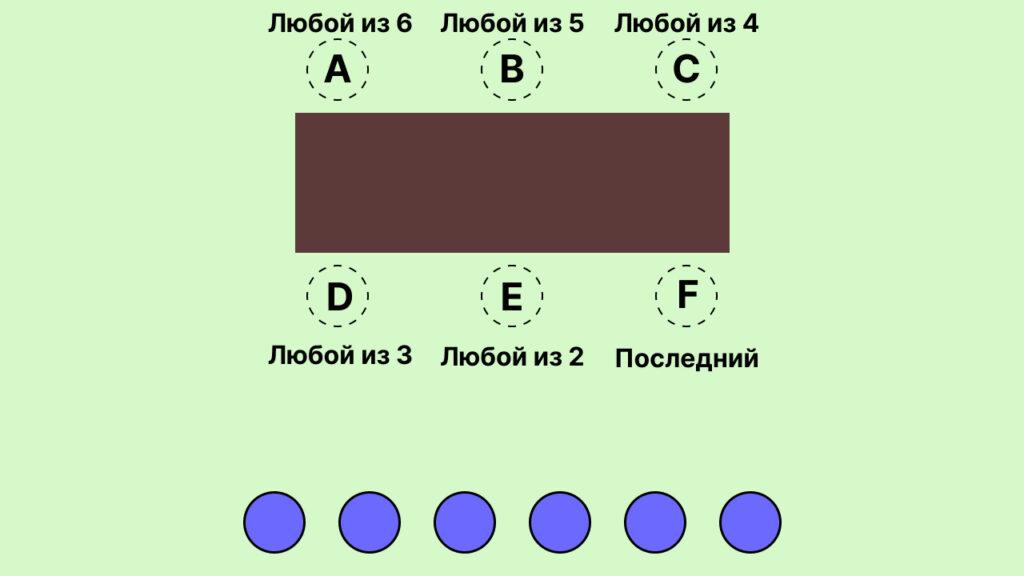
Для того чтобы узнать все способы рассадки гостей, надо перемножить возможные варианты, записанные в изображении над местами. Получим 6 × 5 × 4 × 3 × 2 × 1. Это же выражение можно записать в виде 6!, что равно 720.

Практические задачи

Теперь мы знаем достаточно для решения задач на нахождение факториала. Важно помнить, что можно упрощать факториалы, раскрывать краткую запись, сворачивать полную, сокращать и перемножать. 

Задача 1

Сократите дробь:

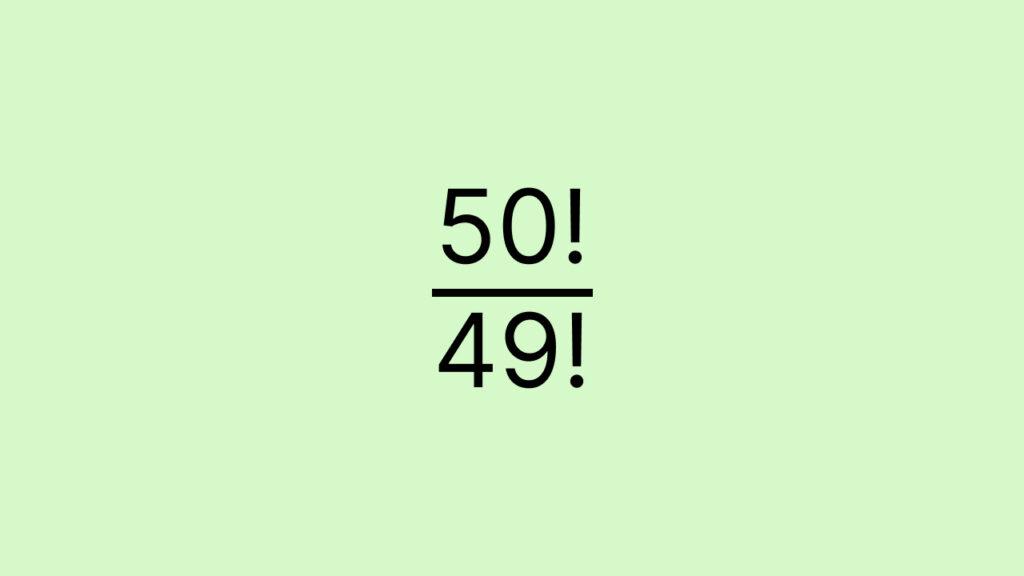
Для решения задачи воспользуемся рекуррентным свойством факториала и разложим числитель. Получившиеся значения в числителе и знаменателе можно сократить, останется 50.

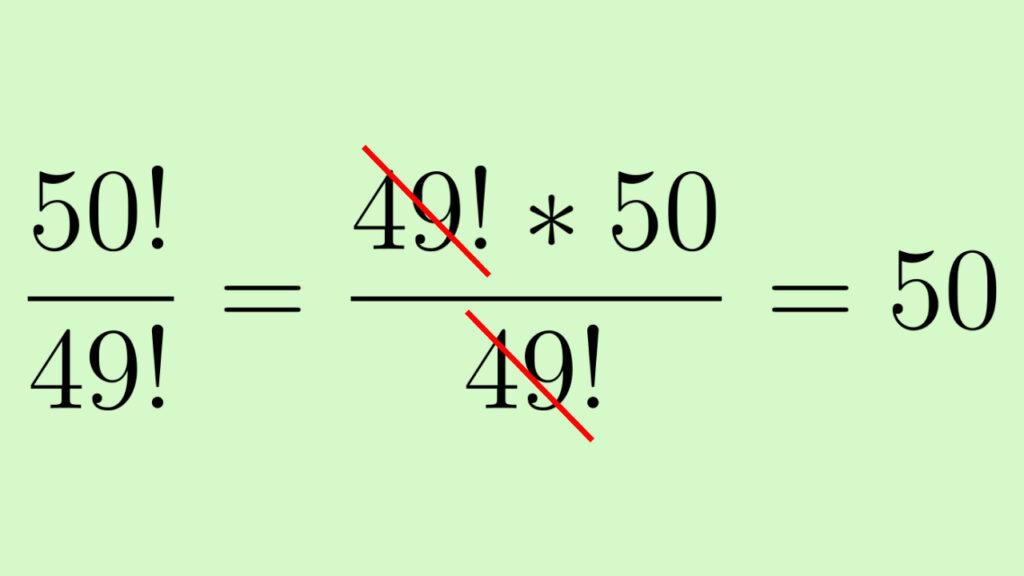
Задача 2

Найдите значение выражения при n=5:

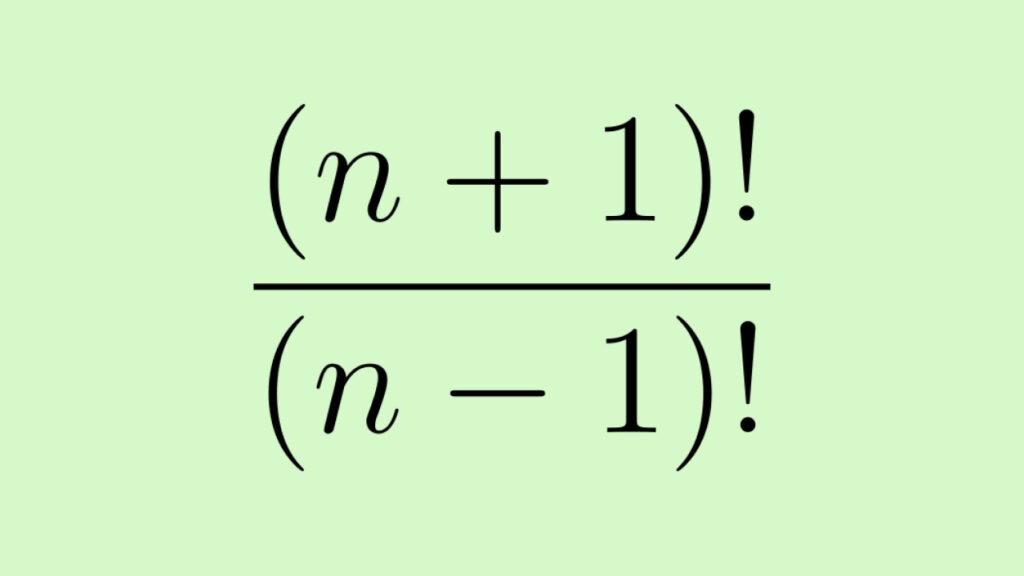
Подставим значения и посчитаем скобки, получившийся числитель можем разложить по рекуррентной формуле, чтобы выражение выглядело как 6 × 5 × 4!. Сократим лишнее и получим 6 × 5 = 30:

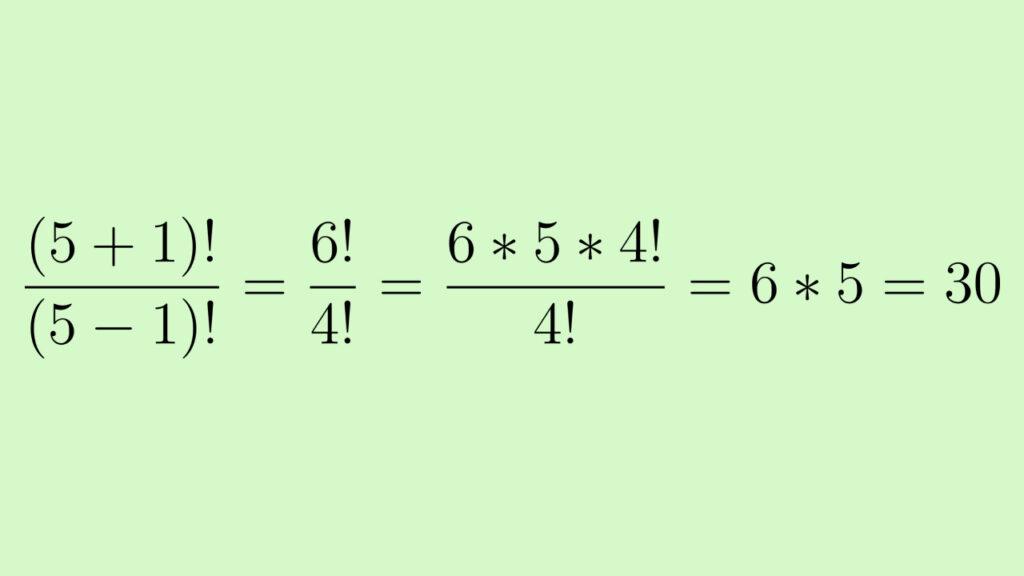
Задача 3

Найдите сумму факториалов чисел от 1 до 5:

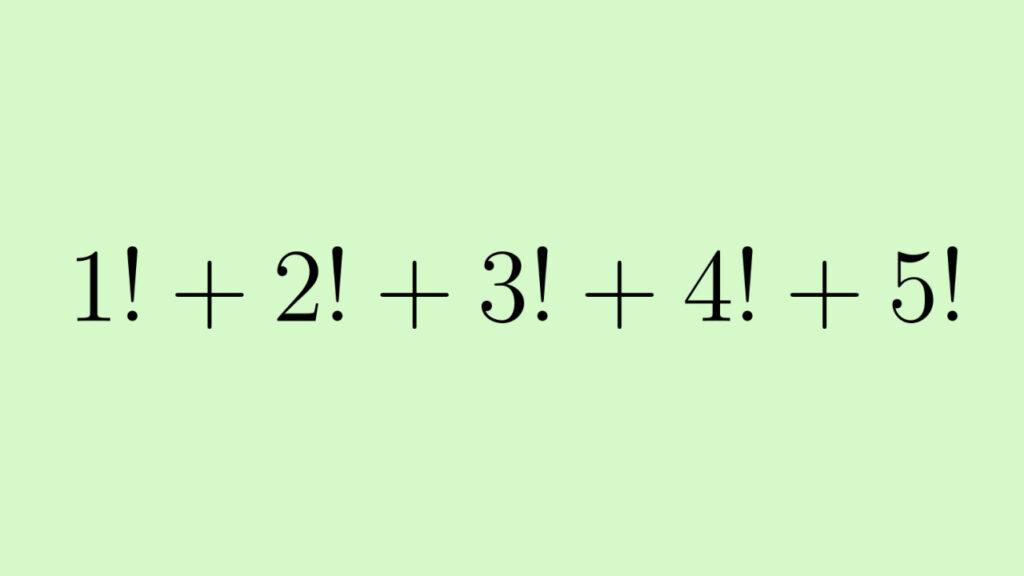
Найдем факториал каждого числа и посчитаем сумму слагаемых:

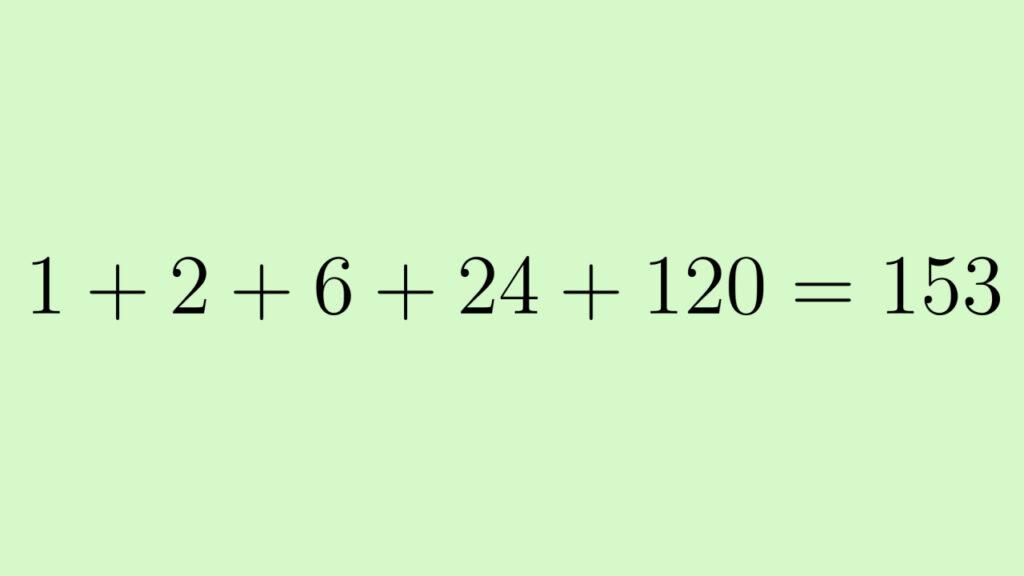
Задача 4

Найдите значение выражения:

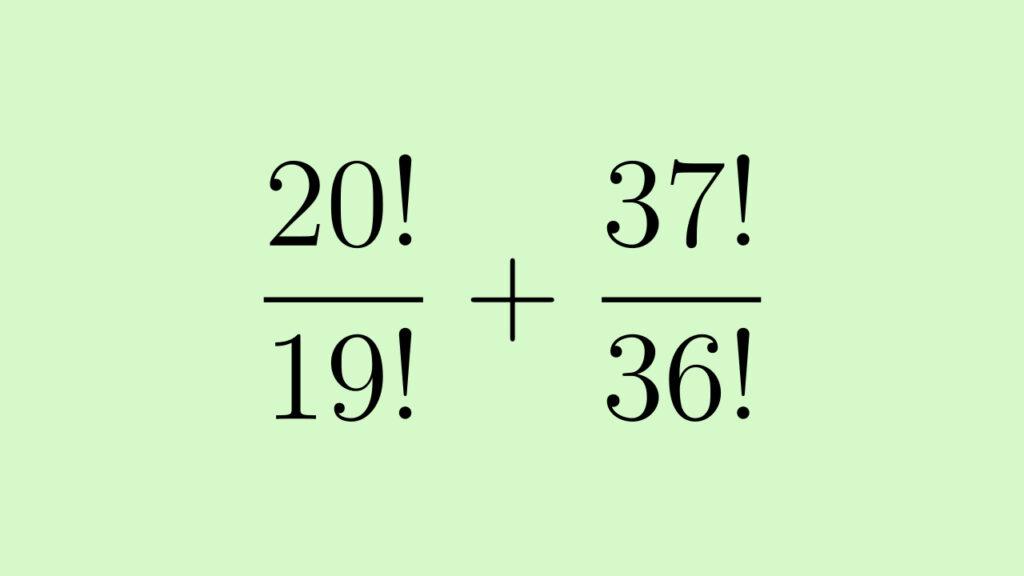
Разложим оба числителям по рекуррентной формуле факториала:

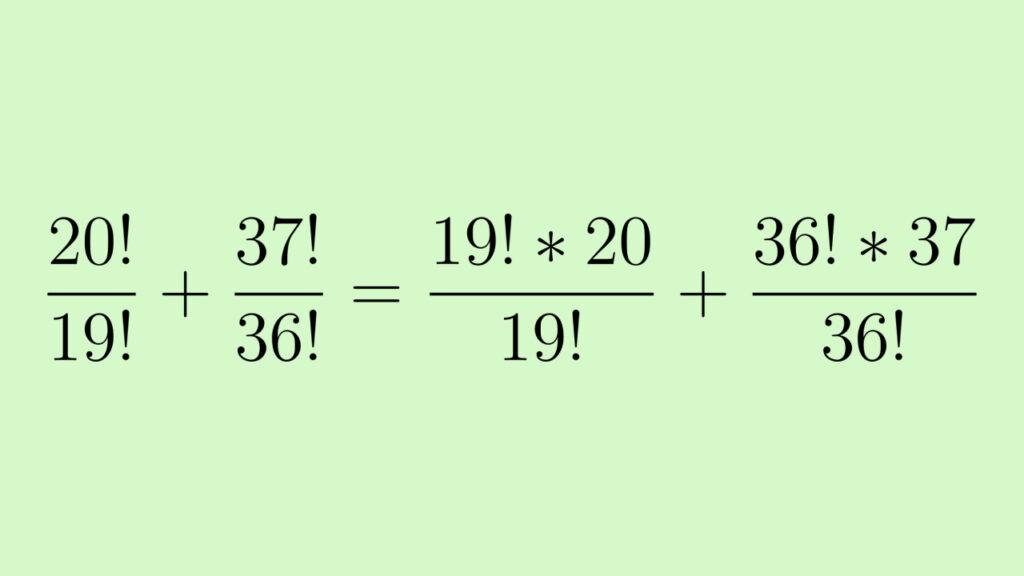
Сократим и умножим, получив в ответе 57:

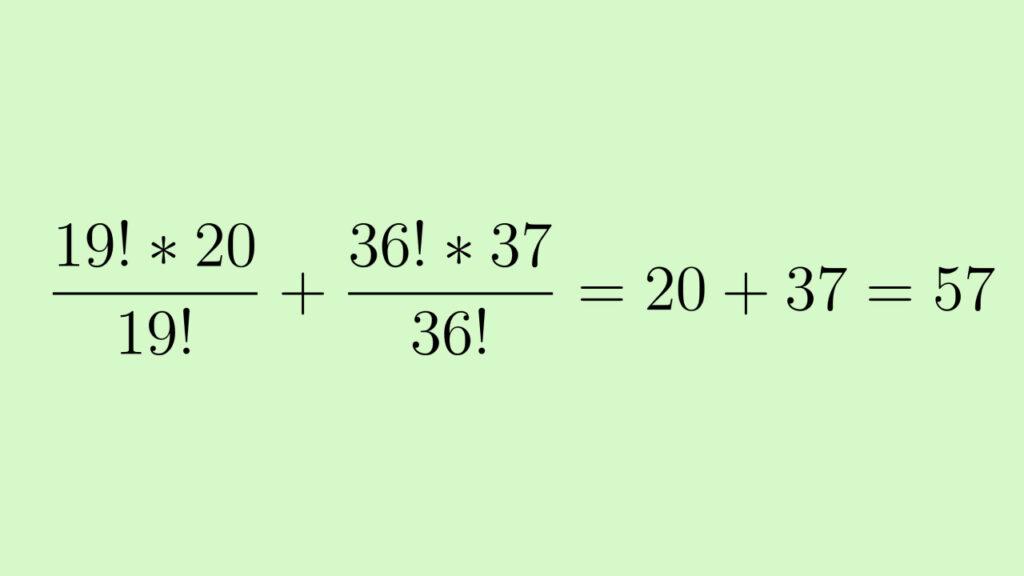
Итог

• Факториал натурального числа n — произведение натуральных чисел от 1 до n.
• Факториал нуля и единицы всегда равны одному — 0! = 1 и 1! = 1.
• Для отрицательных и дробных чисел нельзя вычислить факториал;
• Факториал — быстрорастущая функция, из-за чего сложно находить значения для больших чисел.
• Быстро посчитать факториал можно с помощью формулы Стирлинга, но значение будет приближённым.