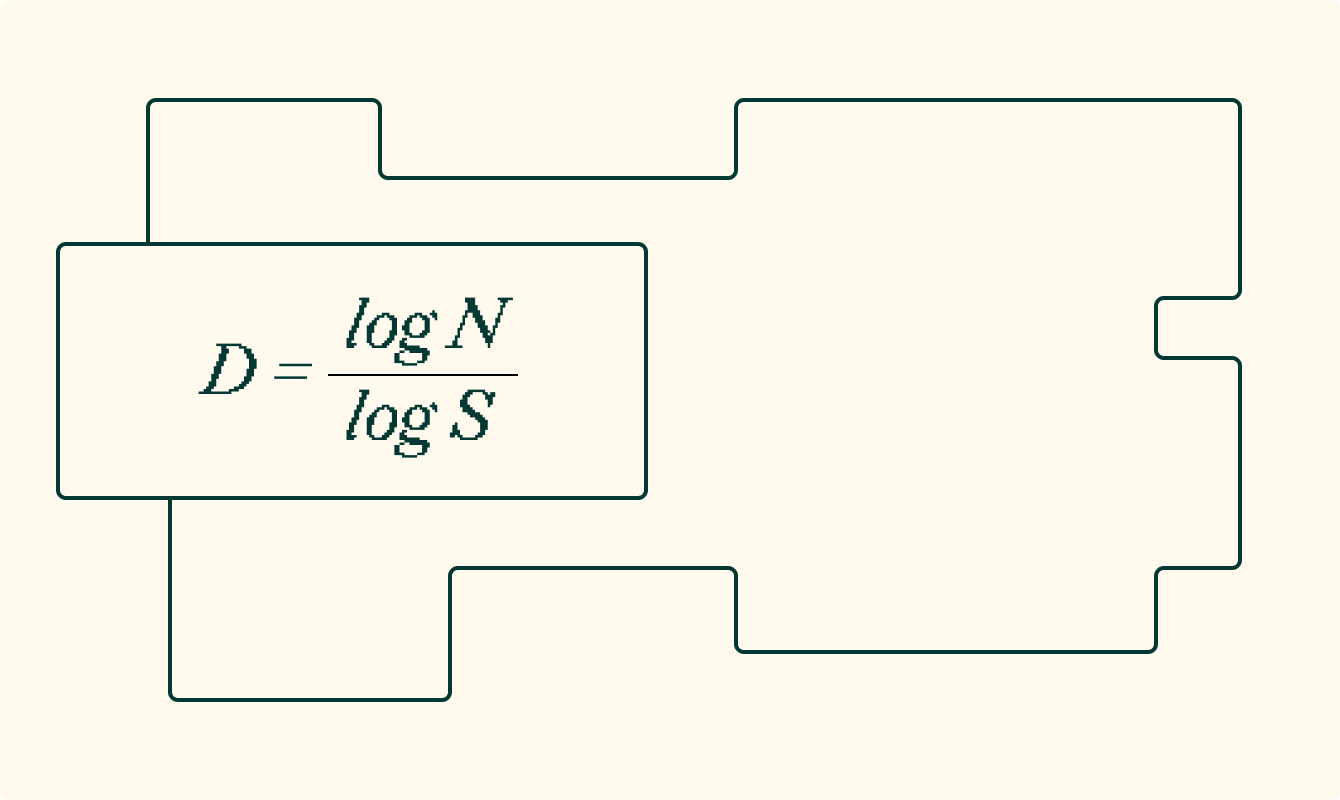Фрактальная размерность: что это и как вычислить

Фрактальная размерность описывает сложность объектов, которые нельзя измерить обычными параметрами, такими как длина или площадь. Например, снежинка при увеличении не становится проще — каждая ее деталь открывает еще более мелкие элементы.

В статье объясняем, что такое фрактальная размерность, и разбираем основные методы ее вычисления. 

Фрактальная размерность: основные понятия

Размерность — это характеристика объекта, которая показывает, сколько параметров нужно, чтобы его описать.

• Нулевая размерность — точка. У нее нет длины, ширины или высоты, поэтому ее размерность равна нулю.
• Одномерная размерность — линия. У нее есть только длина, и для описания точки на линии нужен один параметр, например координата.
• Двумерная размерность — плоскость. Объект имеет длину и ширину. Чтобы описать точку на плоскости, нужны две координаты — x и y.
• Трехмерная размерность — пространство. Оно включает длину, ширину и высоту. Для определения точки в пространстве используются три координаты: x, y и z.

Для измерения сложных и раздробленных объектов используют фрактальную размерность.

Фрактальная (дробная) размерность — это показатель, который помогает описывать сложные объекты, такие как береговые линии, горные рельефы, облака или снежинки. Эти объекты обладают сложной структурой, которая становится более детализированной при увеличении масштаба. Классических параметров, вроде длины или площади, недостаточно, чтобы точно описать такие формы.

Например, если смотреть издалека на береговую линию, она кажется плавной. Но при увеличении масштаба мы замечаем больше мелких изгибов, из-за чего измеряемая длина увеличивается. Этот процесс может продолжаться до тех пор, пока шаг измерения не станет минимально возможным. Таким образом, длина береговой линии не фиксирована и зависит от точности измерений.

Подобные объекты, обладающие сложной, раздробленной формой, можно анализировать с помощью концепции фракталов.

Фрактал — объект, который при увеличении масштаба сохраняет свою самоподобную структуру или становится еще более детализированным. 

Фрактальная размерность же показывает, насколько сильно фрактал заполняет пространство, в котором он существует, измеряет степень его «шероховатости», или «раздробленности».

Если обычная линия имеет размерность 1 (одномерная), плоскость — 2 (двумерная), то фрактал чаще всего имеет дробную размерность, например 1,16 или 1,48.

Общая формула расчета фрактальной размерности

Основная идея состоит в том, чтобы разбить фрактал на элементы заданного масштаба и определить, как изменяется их число при уменьшении размеров.

Общее представление фрактальной размерности выглядит так:

\[ D = \frac{\log N}{\log S}, \]

где:

• D — фрактальная размерность, показатель сложности и структуры объекта;
• log N — логарифм числа элементов, необходимых для покрытия фрактала. По мере уменьшения масштаба размер элементов уменьшается, а их количество увеличивается;
• log S — логарифм обратного масштаба (размера элементов). Чем меньше элемент, тем больше их требуется для покрытия всей структуры.

Примеры фракталов

Треугольник Серпинского

Для наглядного примера и визуализации формулы фрактальной размерности рассмотрим треугольник Серпинского — пример строго самоподобного фрактала.

Он строится путем деления равностороннего треугольника на четыре меньших, после чего центральный треугольник удаляется. Оставшиеся три треугольника повторно делятся по тому же принципу. Этот процесс продолжается на каждом шаге, формируя сложный узор, состоящий из все большего числа треугольников.

Стороны каждого из трех новых треугольников равны 1/2 длины стороны исходного треугольника. Каждый маленький треугольник, если его увеличить в 2 раза, идентичен исходному треугольнику.

Формула треугольника выглядит так:

\[ N = S^D, \]

где:

• N — количество частей, на которые треугольник делится при каждом увеличении масштаба; 
• S — коэффициент уменьшения масштаба (насколько уменьшаются стороны каждой части);
• D — фрактальная размерность.

В данном случае:

• N = 3, так как треугольник делится на три самоподобные части;
• S = 2, так как стороны уменьшаются в 2 раза.

Если выразить из этой формулы D, то получится формула фрактальной размерности:

\[ D = \frac{\log N}{\log S} = \frac{\log 3}{\log 2} \approx 1,585. \]

Получаем, что фрактальная размерность треугольника Серпинского равна 1,585.

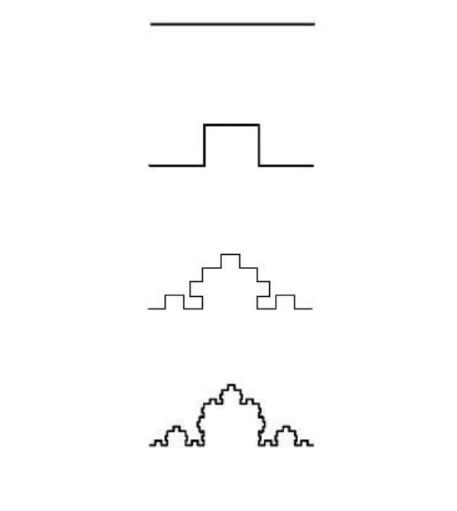
Кривая Коха

Пример строго самоподобного фрактала с самоаффинной природой. Он строится на отрезке, который делится на три равные части, затем на средней части создается «пик» в форме равностороннего треугольника без основания. В результате каждый исходный отрезок заменяется на 4 меньших.

Коэффициент уменьшения масштаба равен S = 3, так как длина каждого нового отрезка составляет ⅓ от первоначального. Таким образом, N = 4, поскольку каждый отрезок заменяется четырьмя новыми.

Используем классическую формулу фрактальной размерности и подставим в нее значения для кривой Коха:

\[ D = \frac{\log N}{\log S} = \frac{\log 4}{\log 3} \approx 1,2619. \]

Фрактальная размерность кривой Коха равна 1,2619.

Как это работает:

1. Начинаем с прямого отрезка.
2. На первом шаге делим его на 3 равные части. Среднюю часть заменяем равносторонним треугольником без основания. В результате получаем 4 отрезка одинаковой длины, каждый из которых составляет ⅓ ​ длины исходного отрезка.
3. На каждом следующем шаге повторяем ту же процедуру для каждого из новых отрезков: заменяем каждый из них на 4 меньших по тому же принципу.
4. Этот процесс продолжается бесконечно. Итоговая линия становится все более сложной, ее длина увеличивается с каждым шагом, но фрактальная размерность остается фиксированной и равна 1,2619.

Методы вычисления фрактальной размерности

Метод коробок (box-counting method)

Способ вычисления фрактальной размерности, применимый к любым фрактальным объектам, независимо от их формы и наличия строгого самоподобия. Он заключается в покрытии объекта сетью из «коробок» (обычно квадратов или кубов одинакового размера). Размер коробок постепенно уменьшается, и это позволяет определить, как изменяется их число в зависимости от масштаба.

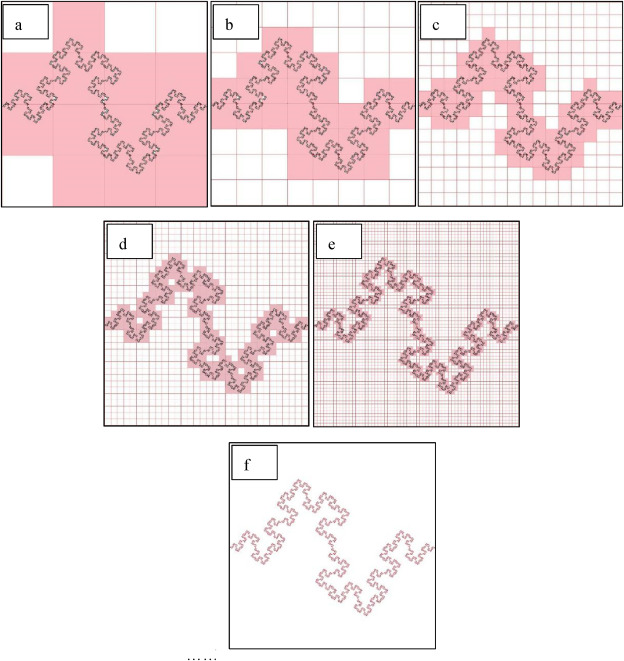
Этот метод особенно удобен для объектов, не имеющих строгой самоподобной структуры, например облака и горные рельефы.

Формула:

\[ D = \frac{\log N(\epsilon)}{\log \left( \frac{1}{\epsilon} \right)}, \]

где:

\(\boldsymbol{\mathrm{D}}\) — фрактальная размерность;
\(\boldsymbol{\epsilon}\) — размер стороны каждой коробки (чем меньше, тем точнее результат);
\(\boldsymbol{\log N(\epsilon)}\) — логарифм от числа коробок. Этот параметр показывает, насколько сильно вырастет количество коробок, необходимых для покрытия объекта, по мере уменьшения их размера;
\(\boldsymbol{\mathrm{log} \left(\frac{1}{\epsilon}\right)}\) — логарифм обратного значения стороны коробки. Это выражение показывает, как уменьшается размер коробок при увеличении масштаба.

Как это работает:

1. Рисуем на объекте крупную сетку и считаем, сколько коробок необходимо для покрытия всех её точек.
2. Уменьшаем размер коробок, увеличиваем их количество и снова считаем, сколько их требуется.
3. Повторяем процесс несколько раз, фиксируя значения \(\mathrm{N}(\mathrm{\epsilon})\) для разных размеров \(\mathrm{\epsilon}\).
4. Строим график зависимости \(\mathrm{log} \, \mathrm{N}(\mathrm{\epsilon})\) от \(\mathrm{log} \left(\frac{1}{\mathrm{\epsilon}}\right)\) и находим наклон линии, который и будет фрактальной размерностью \(\mathrm{D}\).

Размерность Минковского

Этот метод, также называемый размерностью покрытия, помогает определить, как объект заполняет пространство. Для этого его покрывают сеткой из ячеек одинакового размера и подсчитывают их количество. Затем размер ячеек уменьшают и снова считают, фиксируя, как изменяется их число. Эти данные используются для расчета фрактальной размерности.

Как это работает:

1. Выбираем фигуру. Начинаем с фигуры, например квадрата \(\mathrm{l}^2\) или куба \(\mathrm{l}^3\), сторона которых равна 1.
2. Определяем длину сторон ячеек. Берем любое натуральное число \(k\) и устанавливаем длину стороны ячейки как \(s = \frac{1}{k}\).
3. Покрываем фигуру ячейками. Квадрат заполняется квадратами со стороной \(s\), а куб — кубами того же размера.
4. Подсчитываем общее число ячеек:
— Для квадрата \(\mathrm{l}^2\) используем \(k^2 = \frac{1}{s^2}\) ячеек, чтобы полностью покрыть его.
— Для куба \(\mathrm{l}^3\) используем \(k^3 = \frac{1}{s^3}\) ячеек для покрытия.
5. Рассчитываем размерность. Она определяется как показатель степени в зависимости между количеством ячеек и их размером:
\[
\mathrm{N} = \left(\frac{1}{s}\right)^{\mathrm{D}},
\]
где \(\mathrm{D}\) — размерность фигуры. Для квадрата это \(\mathrm{D} = 2\), а для куба \(\mathrm{D} = 3\), что соответствует их привычным геометрическим характеристикам.

Формула для размерности куба будет выглядеть так:
\[
\mathrm{D} = \frac{\mathrm{log} \left(\frac{1}{s^3}\right)}{\mathrm{log} \left(\frac{1}{s}\right)} = \frac{-3 \, \mathrm{log}(s)}{\mathrm{log}(s)} = 3
\]

Пример для конечного множества точек:

1. Возьмем конечное множество \( \mathrm{X} = \{p_1, \dots, p_d\} \subset \mathbb{R}^n \), состоящее из \( d \) точек, чтобы вычислить размерность Минковского.

2. Покрываем множество ячейками. Чтобы покрыть каждую точку множества \( \mathrm{X} \), достаточно поместить одну ячейку на каждую из них. Таким образом, для любой длины стороны ячейки \( \epsilon > 0 \) количество ячеек \( f(\epsilon) \), необходимых для покрытия множества, будет равно количеству точек, то есть \( f(\epsilon) = d \).

3. Вычисляем размерность. Размерность Минковского определяется пределом при \( \epsilon \to 0 \) от выражения:
\[
\frac{\mathrm{log}(f(\epsilon))}{\mathrm{log}\left(\frac{1}{\epsilon}\right)} = \frac{\mathrm{log}(d)}{\mathrm{log}\left(\frac{1}{\epsilon}\right)} = 0.
\]

4. Полученная размерность равна 0. Это логично, так как конечное множество точек не имеет протяженности в пространстве и, следовательно, его размерность равна нулю.

Практический пример на Python

В теории мы разобрались, что фрактальная размерность позволяет количественно оценить самоподобие и комплексность объектов. 

Теперь рассмотрим, как можно применять методы вычисления фрактальной размерности на Python. Для этого будем использовать библиотеки NumPy для вычислений и Matplotlib — для визуализации.

Импортировать NumPy можно с помощью строки:

import numpy as np

Документацию по Matplotlib можно найти на официальном сайте, а для визуализации нужно импортировать библиотеку:

import matplotlib.pyplot as plt

Рассмотрим вычисление фрактальной размерности на примере треугольника Серпинского.

Цель — построить треугольник Серпинского и рассчитать его фрактальную размерность методом коробок.

Задаем начальные вершины большого треугольника:

vertices = [[0, 0], [1, 0], [0.5, np.sqrt(3)/2]]

Создаем треугольник Серпинского с помощью функции:

def sierpinski_triangle(vertices, depth):
    if depth == 0:
        return [vertices]
    else:
        # Находим средние точки сторон
        middle_points = [
            [(vertices[0][0] + vertices[1][0]) / 2, (vertices[0][1] + vertices[1][1]) / 2],
            [(vertices[1][0] + vertices[2][0]) / 2, (vertices[1][1] + vertices[2][1]) / 2],
            [(vertices[2][0] + vertices[0][0]) / 2, (vertices[2][1] + vertices[0][1]) / 2],
        ]
        # Рекурсивно строим три новых треугольника
        triangles = []
        triangles += sierpinski_triangle([vertices[0], middle_points[0], middle_points[2]], depth-1)
        triangles += sierpinski_triangle([middle_points[0], vertices[1], middle_points[1]], depth-1)
        triangles += sierpinski_triangle([middle_points[2], middle_points[1], vertices[2]], depth-1)
        return triangles

Пишем функцию для рисования треугольника:

def plot_sierpinski(vertices, depth):
    triangles = sierpinski_triangle(vertices, depth)
    plt.figure(figsize=(8, 8))
    for triangle in triangles:
        x = [triangle[0][0], triangle[1][0], triangle[2][0], triangle[0][0]]
        y = [triangle[0][1], triangle[1][1], triangle[2][1], triangle[0][1]]
        plt.plot(x, y, color="black")
    plt.gca().set_aspect('equal', adjustable='box')
    plt.axis('off')
    plt.show()

Вызываем функцию построения треугольника с глубиной 4:

plot_sierpinski(vertices, depth=4)

Глубина в данном случае означает количество итераций (или уровней рекурсии), на которые разбивается фрактал для его построения.

Получается такая визуализация:

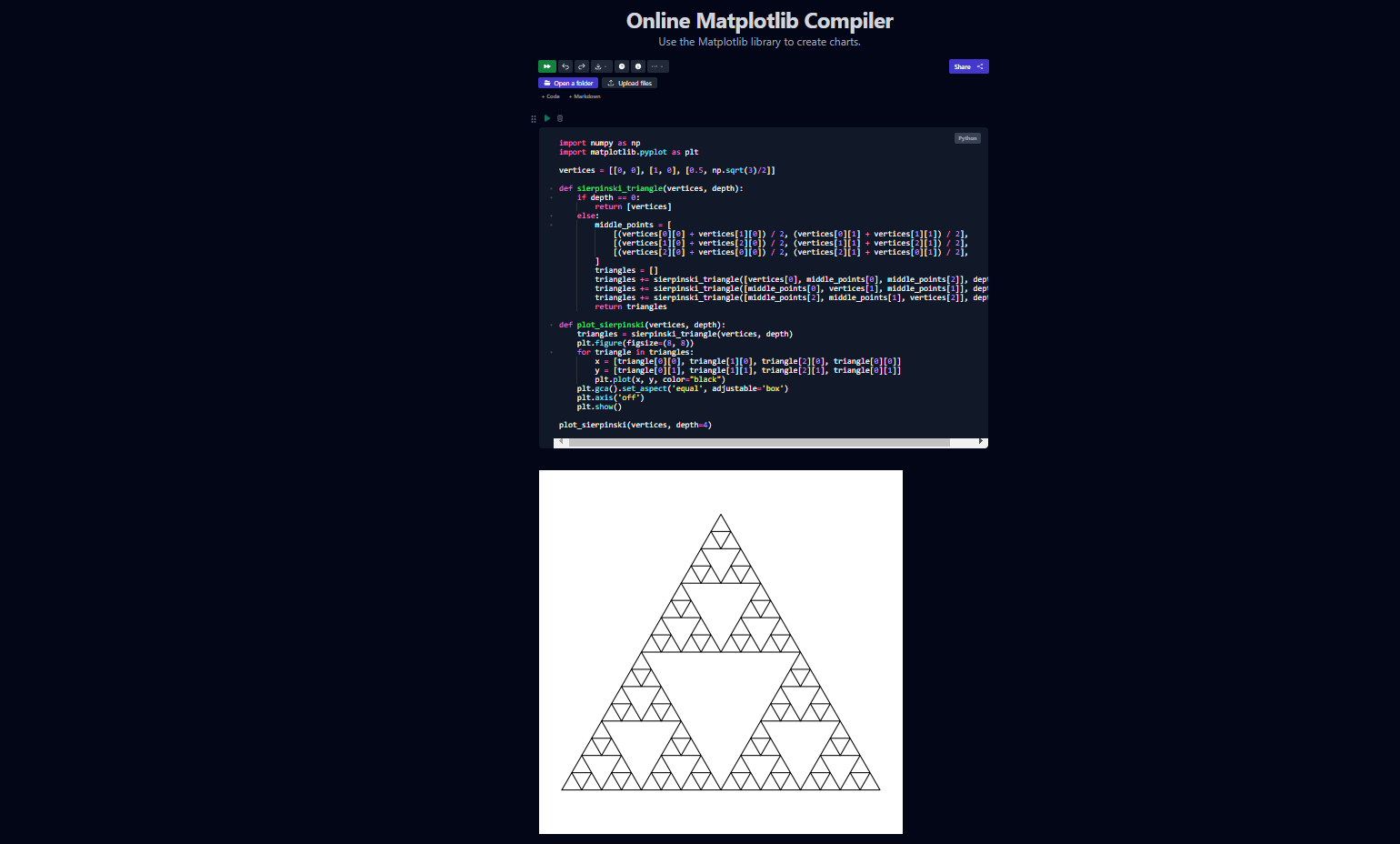
Применяем метод коробок.

Рассчитаем количество коробок, необходимых для покрытия фрактала при разных масштабах, а из этих данных вычислим фрактальную размерность, используя логарифмическую регрессию.

def count_boxes(triangles, box_size):
    count = 0
    for triangle in triangles:
        # Находим координаты для каждого треугольника
        x_min, x_max = min([p[0] for p in triangle]), max([p[0] for p in triangle])
        y_min, y_max = min([p[1] for p in triangle]), max([p[1] for p in triangle])
        
        # Проверяем, сколько коробок размером box_size нужно для покрытия треугольника
        if (x_max - x_min) <= box_size and (y_max - y_min) <= box_size:
            count += 1
    return count

Вычислим фрактальную размерность с использованием метода коробок:

def calculate_fractal_dimension(vertices, depth):
    triangles = sierpinski_triangle(vertices, depth)
    
    box_sizes = []
    box_counts = []
    
    # Уменьшаем размер коробки на каждом шаге
    for i in range(1, depth + 1):
        box_size = 1 / (2 ** i) # Размер коробки для этого уровня
        box_sizes.append(box_size)
        
        # Подсчитываем количество коробок для покрытия фрактала
        box_count = count_boxes(triangles, box_size)
        box_counts.append(box_count)
    
    # Применяем логарифмическую регрессию
    log_box_sizes = np.log(box_sizes)
    log_box_counts = np.log(box_counts)
    
    # Строим график
    plt.figure(figsize=(8, 8))
    plt.plot(log_box_sizes, log_box_counts, 'o-', label='Box counting')
    plt.xlabel('log(Box Size)')
    plt.ylabel('log(Box Count)')
    plt.title('Fractal Dimension of Sierpinski Triangle')
    plt.show()
    
    # Расчет фрактальной размерности как наклон графика
    coefficients = np.polyfit(log_box_sizes, log_box_counts, 1)
    fractal_dimension = coefficients[0]
    
    return fractal_dimension

Получим фрактальную размерность для треугольника Серпинского с глубиной 4 и выведем результат:

fractal_dimension = calculate_fractal_dimension(vertices, depth=4)

print(f"Фрактальная размерность треугольника Серпинского: {fractal_dimension}")

В результате получим 1,585, что является фрактальной размерностью треугольника Серпинского.

График фрактальной размерности будет выглядеть следующим образом:

Описание функций

1. Функция sierpinski_triangle (vertices, depth). Рекурсивно строит треугольники Серпинского. Начинается с треугольника, заданного вершинами, и на каждом шаге делит каждый треугольник на три новых, используя средние точки его сторон.
   
   Аргументы:

• vertices — список из трех точек, задающих вершины исходного треугольника.
• depth — глубина рекурсии (насколько глубоко нужно делить треугольник).

2. Функция plot_sierpinski (vertices, depth). Рисует фрактал треугольника Серпинского с заданной глубиной. Она вызывает функцию sierpinski_triangle для генерации треугольников, а затем использует matplotlib для их отображения.
   
3. Функция count_boxes (triangles, box_size). Вычисляет количество коробок, которые необходимы для покрытия всех треугольников на текущем уровне.
   
   Аргументы:

• triangles — треугольники, для которых нужно посчитать количество коробок.
• box_size — размер коробки.

4. Функция calculate_fractal_dimension (vertices, depth). Вычисляет размерность фрактала, используя метод коробок (box-counting method).
   
   Аргументы:

• vertices — вершины исходного треугольника.
• depth — глубина рекурсии для построения фрактала.

С помощью логарифмической регрессии мы получили фрактальную размерность треугольника Серпинского. Значение подтверждает, что фракталы могут иметь нецелочисленные размерности.