Ориентированный граф

Ориентированный граф — один из видов графа, структуры, состоящей из вершин и путей между ними. Используется в математике и программировании. Проще всего представить граф в виде карты с городами: вершины — это города, а пути — дороги между ними. В ориентированном графе все дороги односторонние.

Что такое графы и какими они бывают

Графы — это абстракция для представления отношений между сущностями. С ее помощью можно описать дорожную карту, сеть из нескольких модулей, программу и пр. Сам граф описывается как точки и соединяющие их отрезки либо с помощью математических формул.

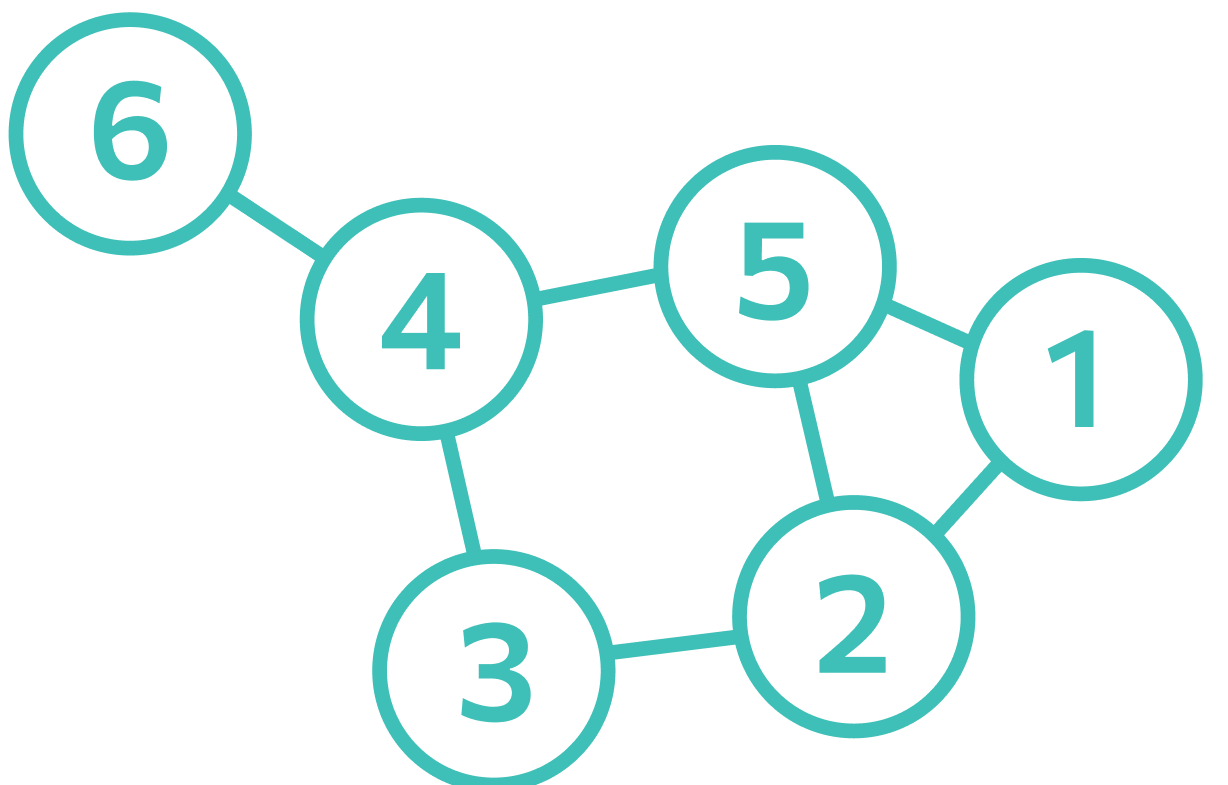
Отрезки между вершинами могут быть неориентированными, а могут иметь направление. Если ребро имеет направление, его изображают не отрезком, а стрелкой между двумя точками. Ориентированным называют такой граф, у которого все пути направленные.

Фактически направление означает, в каком порядке можно обходить структуру. По неориентированным путям можно проходить в любую сторону — от вершины A к вершине B и наоборот. А если путь ориентированный, по нему можно идти только в направлении стрелки.

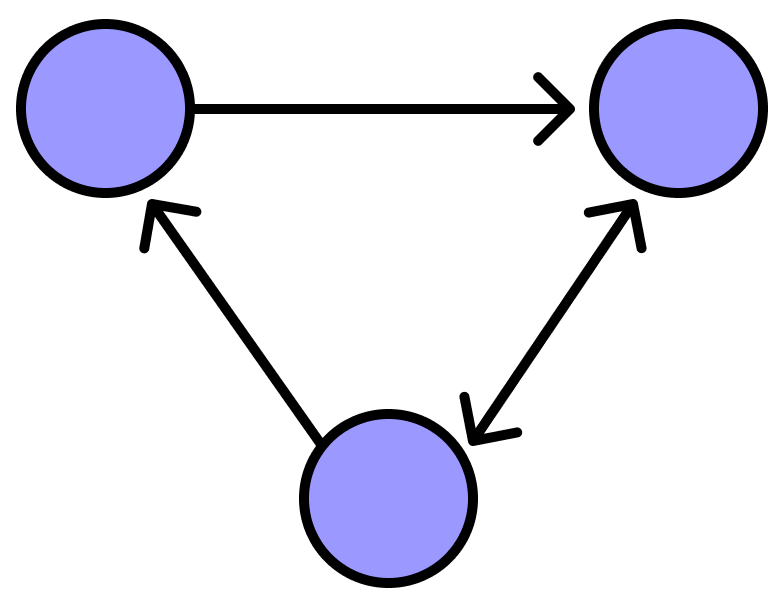
В ориентированном графе по всем отрезкам можно проходить только в одну сторону. Если она из линий выглядит как двойная стрелка, она считается двумя «дорогами», направленными в разные стороны.

Для чего нужны ориентированные графы

На основе графов создают модели тех или иных процессов, событий, взаимоотношений или объектов.

Графы как концепция используются в точных, естественных и гуманитарных науках: от физики и химии до экономики или социологии. С их помощью описывают разнообразные процессы, связи, структуры. Это может быть и схема работы алгоритма, и визуализация социальных взаимоотношений — практически любая структура, которую можно представить как набор элементов и связей между ними.

Поэтому привести полный список примеров использования графов невозможно. Ситуации, в которых может понадобиться граф, встречаются даже в таких дисциплинах, как археология или диспетчерское обслуживание полетов.

Они могут использоваться даже в логических и математических задачах, в головоломках.

Кто пользуется ориентированными графами

• Математики и другие ученые, которые описывают с их помощью явления.
• Инженеры, так как электронные сети и другие похожие схемы тоже можно представить как графы.
• Разработчики, которые пользуются графами как структурой данных или модулей. Структуры бывают нужны при разработке искусственного интеллекта и реализации некоторых алгоритмов.

Понятия, связанные с графами

Это основные термины, связанные с графами в целом. Ниже мы поговорим о понятиях, которые касаются непосредственно ориентированных графов.

• Вершина — одна из точек, из которых состоит граф.
• Ребро — отрезок между двумя вершинами, которым они соединяются.
• Путь — способ пройти от одной вершины к другой без повторения ребер.
• Простой путь — путь, где вершины не повторяются.
• Цикл — участок графа, где вершины образуют замкнутую систему. Визуально это выглядит как многоугольник.
• Связный граф — такой, в котором из любой вершины есть путь к другой.
• Дерево — связный граф, где нет циклов. Эту абстракцию часто используют в программировании для хранения данных и при машинном обучении.
• Полный граф — граф, где все вершины соединены друг с другом.
• Петля — ребро, которое ведет из вершины в нее же. У такого ребра совпадают начало и конец.

Термины для ориентированных графов

Если граф ориентированный и все ребра у него имеют «направление прохода», то при его описании нужны дополнительные понятия.

• Степень выхода вершины ориентированного графа — то, сколько путей-стрелок «выходит» из вершины.
• Степень входа — соответственно, количество «входящих» в вершину стрелок.
• Изолированная вершина — такая, у которой степени входа и выхода равны 0.
• Источник — вершина, у которой степень входа равна 0, а степень выхода больше 0.
• Сток — наоборот, вершина, у которой степень выхода равна 0, а степень входа больше 0.
• Ориентированный цикл — цикл, который состоит из направленных ребер. При этом он по-прежнему должен создавать замкнутый путь.
• Полный ориентированный граф — ориентированный граф, у которого каждая пара вершин соединена ровно одним ориентированным ребром. Это почти то же самое, что простой полный граф, только его ребра должны иметь направление.

Как графы представляются в программировании

Визуальное представление графа, в том числе ориентированного, хорошо понятно человеку. Но компьютер не понимает такую структуру, поэтому в программировании графы реализуют иначе. Их кодируют с помощью одного из двух способов: матрицы смежности или списка смежности.

Матрицы смежности. Матрица — это понятие из математики. Оно означает набор связанных между собой чисел, который представляют в виде двумерной таблицы. Матрицы используются во многих математических формулах и в множестве отраслей, в том числе при описании графа.

Матрица смежности — это способ представить граф в виде подобной таблицы. У нее N столбцов и N строк, где N — количество вершин в графе. Столбцы и строки имеют те же названия или номера, что и вершины.

Заполняется матрица так: если из вершины A в вершину B ведет ребро, то на пересечении строки A и столбца B в таблицу ставится единица. Такое повторяется для всех ребер, а оставшиеся ячейки заполняются нулями.

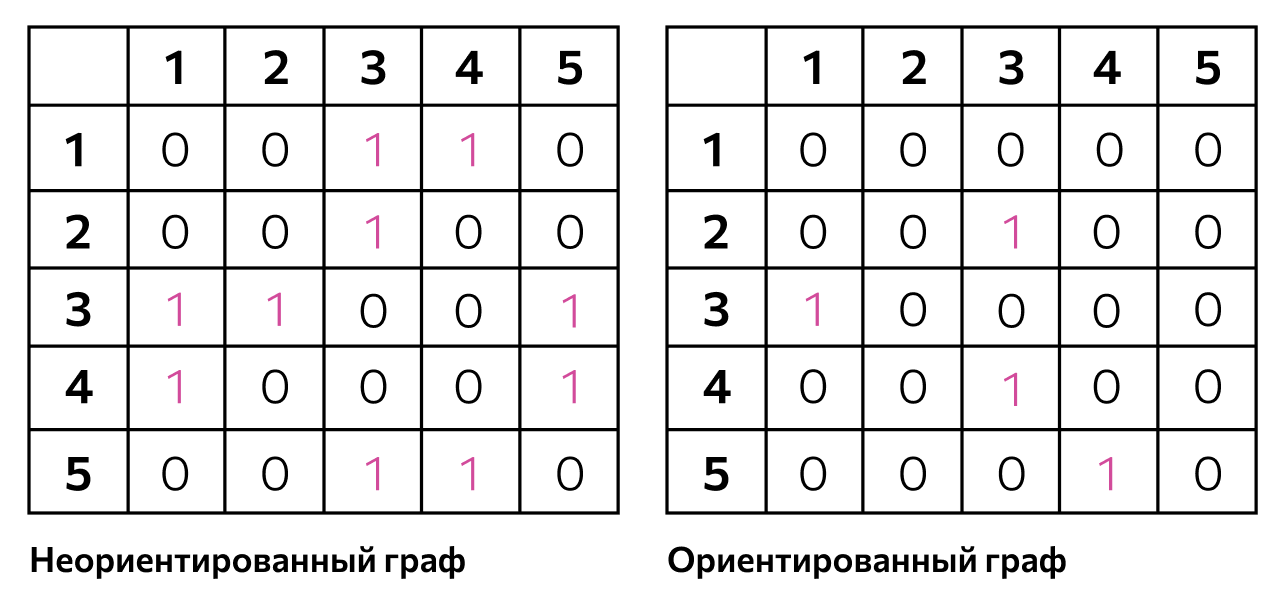
Такой способ описания подходит для ориентированных и неориентированных графов. Это работает, потому что ячейка n[A][B] и ячейка n[B][A] — разные. Благодаря этому можно передать на матрице направления ребер.

Подход используют, если граф плотный: количество ребер примерно равно количеству вершин, возведенному в квадрат. Иначе нулей будет слишком много, и матрица получится громоздкой.

Списки смежности. Это второй способ. Он менее нагляден, но занимает меньше места в памяти. Его используют, если количество ребер намного меньше, чем количество вершин в квадрате, — так называемый разреженный граф. Матрица будет заполненной нулями. Для хранения в памяти компьютера это критично: полезной информации мало, зато структура отнимает много ресурсов. Поэтому при малом количестве ребер используют список.

Список смежности — это N массивов данных, где N — количество вершин. На каждую вершину приходится один массив: в нем содержится имя этой вершины и список ее «соседей». То есть у каждой вершины есть список тех, что соединены с ней ребром.

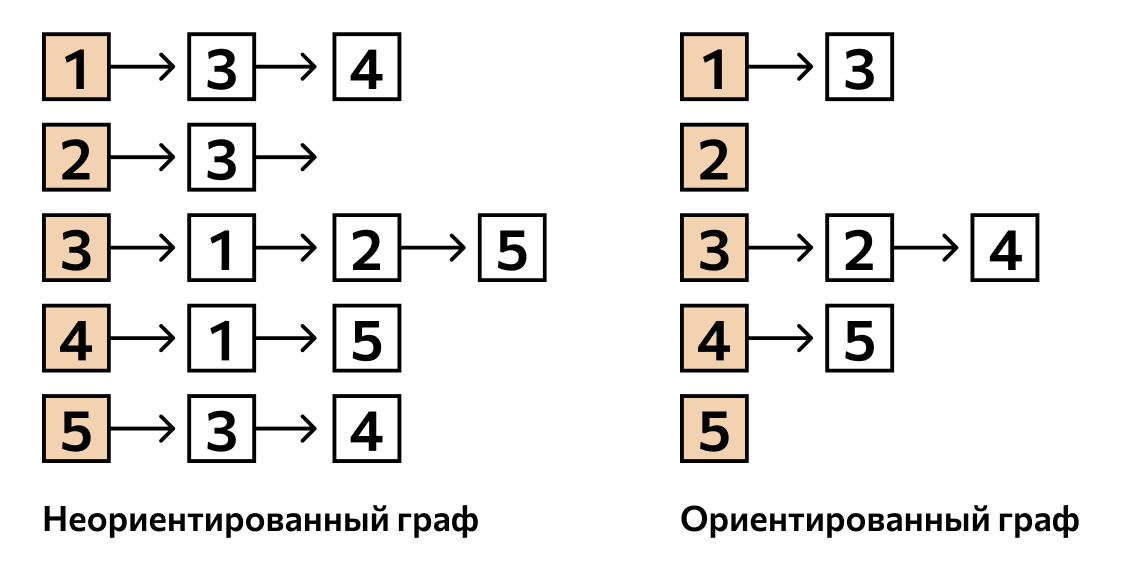
Метод списков смежности опять же подходит и для ориентированных, и для неориентированных графов. Во втором случае списки будут длиннее, потому что соединения придется указывать дважды: A—B — это не только путь из A в B, но и путь из B в A. Поэтому его придется добавить и в массив для A, и в массив для B.

В этом способе представления удобнее узнавать о соседях вершины. Также он занимает меньше памяти, и алгоритмы проходят по нему быстрее. Но он плохо подходит для плотных графов.

Алгоритмы с использованием ориентированных графов

Ориентированные графы используются в десятках алгоритмов в разных сферах IT. Это в первую очередь машинное обучение, анализ данных и другие направления, где используются большие и абстрактные структуры информации. Но встретить графы можно и в других сферах.

Разберем несколько примеров, чтобы вы могли понять, в каких задачах программирования могут применяться ориентированные графы.

Поиск в глубину. Это метод обхода графа, где цель алгоритма — пройти максимально глубоко от первой вершины. Алгоритм подсчитывает расстояние между разными вершинами.

Обход начинается с одной из вершин. Затем алгоритм перемещается в другие вершины по ребрам и помечает каждую из пройденных как посещенную, если ему удается пройти ее без циклов. Для каждой новой вершины шаг повторяется, если она не была посещена раньше. Алгоритм возвращается назад, если в одной из вершин не оказалось ребер, которые вели бы из нее куда-то еще.

Поиск в ширину. Тоже метод обхода графа, частично похожий на предыдущий. Алгоритм обходит вершины, начиная с первой заданной. Но делает он это иначе. Если при поиске в глубину алгоритм последовательно шел «вглубь» графа, то здесь он по очереди переходит к каждому из «соседей» начальной точки. Каждый «сосед» помечается как пройденный. Когда пути из начальной точки закончатся, алгоритм перейдет к обходу «соседей» по такой же методике.

Этот алгоритм помогает, например, найти самый короткий путь передачи данных. Его можно использовать и в других задачах, в том числе при машинном обучении.

Топологическая сортировка. Сортировка — распространенная задача в программировании, для которой существуют десятки известных алгоритмов. Топологическая сортировка на графах — один из них.

Алгоритм нумерует вершины графа так, чтобы из вершины с меньшим номером всегда выходили ребра, ведущие в вершину с большим номером. Такое может понадобиться, например, при упорядочивании сложных структур.

Задача 2-SAT. Это еще одна интересная практическая задача — подстановка значений в формулу таким образом, чтобы она оказалась верной. Формула представляется в виде графа импликаций, где у каждой переменной две вершины — x и !x (не x). Между вершинами проставляются связи в зависимости от условий задачи. Если оказывается, что из x есть путь в !x, а из !x одновременно с этим есть путь в x, то задача решения не имеет.

Алгоритм подходит для решения задач, где неизвестные переменные могут принимать одно из двух противоположных значений. Например, составление расписания спортивных игр: каждая команда должна по разу сыграть с другими командами, может играть дома или на выезде. В реальном мире задач, которые отвечают таким требованиям, намного больше.