Комбинаторика — это база
Комбинаторика — это наука о том, как сочетать и комбинировать различные объекты. С одной стороны, комбинаторика считает количество возможных комбинаций, а с другой — помогает найти комбинацию с оптимальными свойствами. Определение может показаться сложным и запутанным. При этом ежедневно мы применяем комбинаторику в обычной жизни и не замечаем этого. Например, придумываем пароль при регистрации на сайте — комбинацию букв, цифр и знаков — или комбинируем удобные варианты пересадок, когда покупаем авиабилет за границу.
К счастью, комбинаторика подчиняется правилам и принципам. Про них и поговорим.
Правило сложения
Представим, что мы хотим купить велосипед. Интересующая нас модель есть в наличии в пяти офлайн-магазинах и трех онлайн.
Офлайн-магазины — это множество А.
Онлайн-магазины — это множество В.
Значит, мы можем выбирать из восьми вариантов точек покупки: множество А + множество В, то есть 5 + 3 = 8 вариантов.
Правило умножения
А теперь о приятном. Представьте, что вы пришли на бизнес-ланч в ресторан. В меню сказано, что вы можете выбрать суп и горячее. При этом в каждом из разделов по пять блюд. Сколько разнообразных вариантов обеда вы сможете составить?
Итак, тип блюда (салат, суп и горячее) — это множество А.
Пять блюд в каждом типе — это множество В.
Значит, мы можем выбрать: множество А * на множество В, то есть 3 * 5 = 15 вариантов.
Перестановка
Перестановка — это метод последовательного расположения элементов множества. Возьмем три буквы А, Б и В и составим из них комбинации, используя перестановки:
- АБВ
- АВБ
- БАВ
- БВА
- ВАБ
- ВБА
Из трех элементов множества у нас получилось 6 различных комбинаций. Это простой пример, результат перестановки которого можно получить даже вручную. А теперь представьте, что вместо трех букв у нас 10. Чтобы узнать, сколько различных комбинаций получится, необходимо вспомнить про факториал.
Факториал — это кто?
Факториал — это функция. Факториал в математике обозначается восклицательным знаком и означает перемножение чисел от 1 до n.
Например, функция 5! будет означать последовательное умножение 1 на 2, на 3, на 4, на 5.
5!= 1 * 2 * 3 * 4 * 5 = 120
Перестановка без повторяющихся элементов
Теперь, когда мы узнали про факториал, вернемся к задаче с А, Б, В и применим формулу, где:
А, Б, В — элементы множества. Всего 3 элемента, тогда количество комбинаций равно 3!
3!= 1 * 2 * 3 = 6
Так мы подтвердили наши ручные подсчеты. Если букв было бы 10 и все они были разные, мы бы получили 10!= 1*2*3*4*5*6*7*8*9*10 = 3628800 вариантов.
Перемножать вручную необязательно. Можно сохранить таблицу со значениями факториалов разных чисел или воспользоваться инженерным калькулятором.
Перестановка с повторяющимися элементами
В предыдущем примере мы исходили из того, что одна буква повторялась в комбинации всего один раз. Усложним задачу.
Представим слово из тех же 10 букв: ш у р у п о в е р т
В этом слове дважды встречается буква «у», остальные буквы встречаются по одному разу. Чтобы посчитать количество перестановок, мы не можем применить простую формулу 10!, которую использовали в прошлой главе.
Объясним почему. Например:
Поменяем первую и последнюю букву и получим два разных варианта:
ш у р у п о в е р т
т у р у п о в е р ш
А если мы поменяем вторую и четвертую букву в слове, то получим два одинаковых варианта:
ш у р у п о в е р т
ш у р у п о в е р т
Чтобы решить задачу, посчитаем сначала общее число вариантов. Это мы уже умеем:
10! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 3628800 вариантов.
Теперь ищем, сколько раз можно переставить повторяющиеся варианты между собой. Повторяющихся вариантов у нас 2 — две буквы «у» в слове.
2! = 1 * 2 = 2 варианта.
Делим общее число вариантов на число повторяющихся вариантов:
3628800/2=1814400.
Тогда формула будет выглядеть как деление факториала общего числа элементов на факториал повторяющегося числе элементов. Это сложная формула. Важно понять её логику и уметь применять в случае необходимости, при этом запоминать — необязательно. Всегда можно воспользоваться подсказкой из интернета.
Сочетание
Сочетание — это набор элементов, взятых из множества. При этом расположение этих элементов не важно.
Сочетание, как и перестановка, может быть с повторяющимися элементами и без.
Сочетание без повторяющихся элементов
Представим, что вы ждете гостей на чай. Пить чай будут 4 человека, вы решаете порадовать друзей и идёте в кондитерскую покупать булочки.
В булочной, однако, 6 видов изделий: с маком, улитка, бриошь, круассан, коржик и имбирное печенье. Сколько вариантов комбинаций из булочек вы могли бы выбрать, если одинаковые вы брать не хотите?
Сначала посчитаем общее количество вариантов булочек из кондитерской: 6! = 1 * 2 * 3 * 4 * 5 * 6 = 720 вариантов.
Дальше считаем количество комбинаций «невыбираемых» булочек: (6 — 4)! = 2! = 2 варианта.
Теперь считаем количество выбираемых булочек: 4! = 1 * 2 * 3 * 4 = 24 варианта.
Делим общее число вариантов на факториалы выбираемых и «невыбираемых» и получаем:
720/2*24=15 вариантов.
Значит, если вы пришли в кондитерскую с шестью видами изделий и выбираете только 4, то у вас есть ровно 15 вариантов выбора.
Сочетание с повторяющимися вариантами
А теперь представим противоположную ситуацию. Гостей к вам придет намного больше, например 12 человек. А разных булочек в магазине все еще 6 штук. Сколько комбинаций вы сможете выбрать? Применим формулу:
(6+12-1)! / (6-1)! * 12! = 17!/ 5! * 12! = (13 * 14 * 15 *16 * 17)/120 = 742560 / 120 = 6188 вариантов.
Никогда еще выбирать булочки не было так сложно!
Размещение
Последняя функция, которую мы рассмотрим, — это размещение. Если в предыдущем разделе мы выбирали несколько элементов из множества и не смотрели на порядок размещения, то здесь мы выбираем несколько вариантов из множества и размещаем их в различных комбинациях.
Размещение без повторяющихся элементов
Размещение без повторяющихся элементов по смыслу похоже на перестановку, о которой мы говорили в начале статьи. Однако в перестановке мы искали количество перестановок, используя все элементы множества А, В, С: АВС, АСВ и тд.
В формуле размещения мы также ищем число возможных комбинаций, используя несколько элементов множества. Например, нам надо узнать, сколько комбинаций можно составить из множества А, В, С, если по условию нужно использовать всего два символа.
То есть число комбинаций будет равно: 3!/(3-2)!=6
Проверим вручную:
АВ
АС
ВА
ВС
СА
СВ
Размещение с повторяющимися вариантами
Последняя формула — самая простая! Представим, что мы выбираем простой пароль на телефон из четырех чисел.
Первая цифра может быть от 1 до 9. То есть 9 комбинаций.
Вторая, третья, четвертая цифры — аналогично. От 1 до 9, то есть ещё 3 раза по 9 комбинаций.
Тогда формула размещения с повторяющимися элементами выглядит как 9 в степени 4. То есть количество доступных вариантов множества нужно возвести в степень количества выборки.
Кратко о комбинаторике: что такое перестановка, сочетание, размещение
Комбинаторика — это наука о том, как комбинировать элементы, составлять различные сочетания из них и находить оптимальные варианты. Перестановка, сочетание и размещение — это основные понятия комбинаторики, которые используют для решения комбинаторных задач.
Перестановка — это метод последовательного расположения элементов множества. Сочетание — это набор элементов, взятых из множества. При этом расположение этих элементов не важно. А размещение — это упорядоченный набор элементов, выбранных из множества.
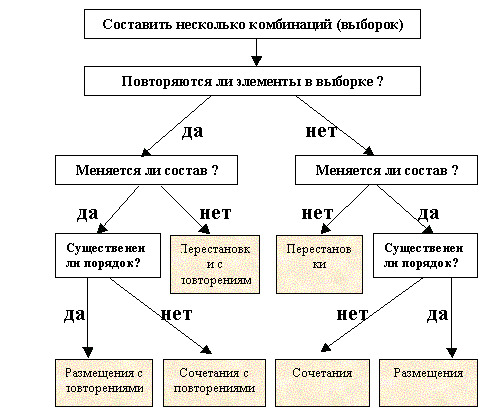
Чтобы понять, какую формулу комбинаторики нужно выбрать для решения конкретной задачи, есть разные шпаргалки. Делимся одной из них: