Расскажем о том, что такое комплексные числа и какие математические операции можно с ними совершать. Покажем на простых примерах, как их складывать, вычитать, умножать и делить. А еще разберемся, как возводить комплексные числа в степень и извлекать из них корни.
Какие бывают числа
Прежде чем говорить о комплексных числах, сначала нужно разобраться с тем, какие вообще бывают числа.
Натуральные и целые числа
Натуральные числа — это числа, используемые для счета. К ним относятся числа от 1 до плюс бесконечности. Например, натуральными являются числа 1, 2, 3, …, 48, …, 126 и так далее. Натуральные числа еще называют целыми положительными числами. Целые числа можно представить как расширение множества натуральных чисел, если к ним добавить нуль и отрицательные числа.
Если с натуральными числами все предельно ясно, то отрицательные числа могут вызывать некоторые вопросы. Любое отрицательное число меньше нуля, а значит, меньше любого положительного числа. Нуль — это пустота, ничто, абсолютный вакуум. Как может существовать что-то меньше, чем ничего? С этим вопросом легко разобраться, если представить отрицательное число как задолженность. Ведь ни у кого не вызывает вопросов, например, отрицательный баланс счета на телефоне или на банковской карте? Вот это и есть то, что меньше нуля.
Рациональные и иррациональные числа
Когда людям понадобилось делить что-то на части, были придуманы дроби. Обыкновенные дроби представляют в таком виде: \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{5}\). Вообще, любое число, которое можно представить в виде обыкновенной дроби \(\frac{m}{n}\), где m — целое число, а n — натуральное, является рациональным. Любое целое число тоже рациональное. Например, число 5 можно записать как \(\frac{25}{5}\) или \(\frac{5}{1}\).
Иррациональные числа нельзя представить в виде обыкновенной дроби. Рациональное число олицетворяет соизмеримость каких-то частей целого. Например, дробь \(\frac{1}{2}\) — это ровно половина от целого, а \(\frac{2}{3}\) — это две третьих части от целого. Иррациональные числа появляются, когда невозможно соизмерить эти самые части. Так, несоизмеримы диагональ и сторона квадрата, равная единице, откуда получается иррациональность числа \(\sqrt 2\). Так же иррационально число , которое является отношением длины окружности к ее диаметру. Основание натуральных логарифмов (число e) тоже иррационально.
Иерархия чисел
Рассмотрим следующий рисунок:
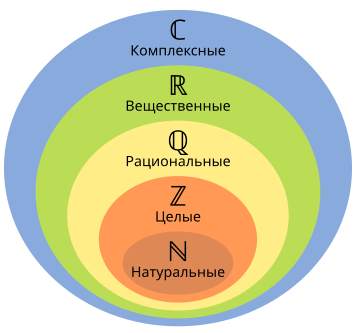
Мы видим, что множество рациональных чисел, включающее в себя множества целых и натуральных чисел, входит во множество вещественных чисел. Их еще называют действительными числами. Натуральные числа появились из потребностей счета, а рациональные — когда возникла необходимость оперировать частями целого.
Множество рациональных чисел не покрывает все точки на числовой прямой. Вот если добавить к рациональным числам еще иррациональные, тогда все точки на числовой прямой будут заняты. Таким образом, можно сказать, что любое действительное число можно представить в виде точки на числовой прямой. Верно и обратное утверждение: любая точка на числовой прямой — это какое-то действительное число:
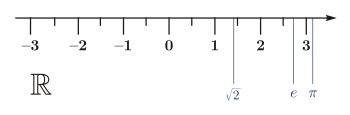
А что с комплексными числами? Как видно из первого рисунка, все вещественные (действительные) числа являются комплексными, но далеко не каждое комплексное число может быть изображено на числовой прямой. Далее мы более подробно разберем этот вопрос.
Что такое комплексные числа
Прежде всего познакомимся с мнимой единицей, так как это важная составляющая комплексного числа.
Мнимая единица
Попробуем решить уравнение \(x^2+1 = 0\). Если перенести единицу в правую часть, то получится, что вторая степень корня уравнения должна быть равна −1:
Как известно, никакое число в четной степени не может в результате дать отрицательное число. Поэтому действительных корней у этого уравнения нет. Но чтобы все же находить корни подобных уравнений, решили ввести понятие мнимой единицы:
То есть мнимая единица i — это не что иное, как квадратный корень из −1. Приведенное выше уравнение будет иметь единственный корень. равный i:
Так как \(i^2= -1\), то \(-1 + 1 = 0\). Получили верное числовое равенство.
Чисто мнимые числа
Примерами чисто мнимых чисел может послужить следующий ряд:
Как видим, это просто мнимая единица, помноженная на какой-либо коэффициент. Такие числа можно складывать, умножать, возводить в степень и тому подобное:
Касательно последнего примера хотелось бы пояснить подробнее. Почему получилось действительное число −6? Потому что мнимая единица была возведена в квадрат \((i \times i)\). А в квадрате она дает −1. Более подробное решение примера:
При возведении чисто мнимых чисел в степень нужно учитывать степени мнимой единицы:
Квадрат: \(i^2= -1\),
Куб: \(i^3 = -1 \times i = -i\),
Четвертая степень: \(i^4 = -1 \times (-1) = 1\),
Пятая степень: \(i^5 = 1 \times i = i\)
Далее ряд значений \((−1, −i, 1, i)\) будет постоянно повторяться. Для примера вычислим куб числа \(-3i\):
Теперь поговорим о комплексных числах.
О комплексных числах
В общем виде комплексные числа записываются как \(z = a+bi\), где a — это действительная часть, b — мнимая часть, а i — мнимая единица. Числа a и b являются действительными. Если a = 0, то комплексное число превращается в чисто мнимое, а если b = 0, то в действительное.
Не нужно думать, что комплексное число — это какая-то сумма. Нет, это единое число, просто в своей алгебраической форме оно представляется именно как результат сложения действительного и чисто мнимого чисел. Но это просто запись и никакого сложения на самом деле не происходит.
Комплексные числа можно изображать на координатной плоскости. Из-за этого их можно представить как двумерные числа. Вот пример двух комплексных чисел на плоскости:
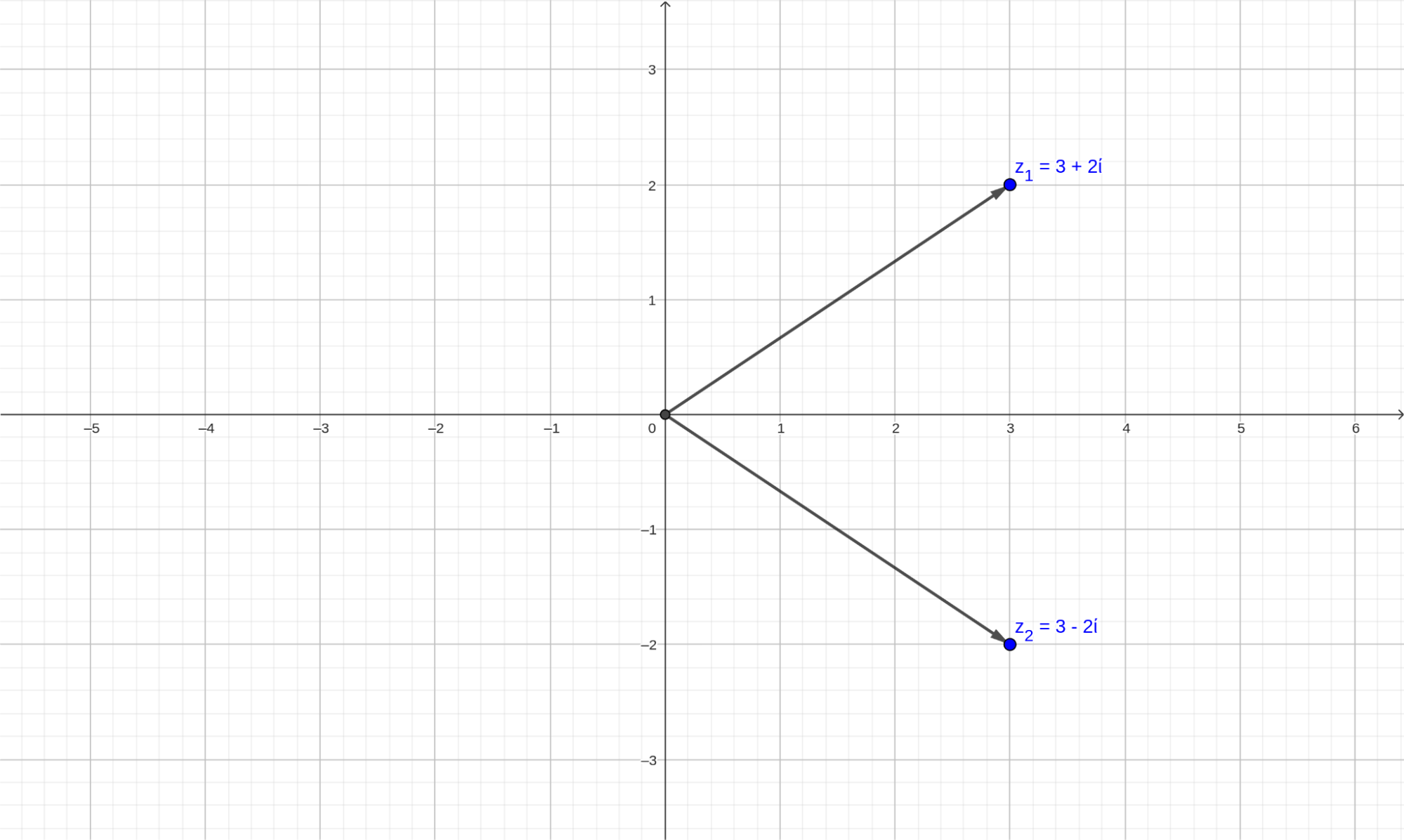
По горизонтальной оси откладывается значение действительной части числа, а по вертикальной — мнимой. Таким образом, на действительной оси находятся действительные числа, а на мнимой — чисто мнимые. Комплексным числам на этих осях места нет, поэтому они занимают всю оставшуюся координатную плоскость.
На представленном выше рисунке изображены два комплексных числа \(z_1 = 3+2i\) и \(z_2 = 3-2i\). Такие числа называются сопряженными. Вообще, если дано число \(z_1 = a+bi\), то число \(z_2 = a-bi\) будет с ним сопряжено, и наоборот.
Ранее упоминавшаяся алгебраическая форма комплексного числа имеет вид \(z = a+bi\), но кроме нее существуют еще тригонометрическая и показательная формы. О них мы поговорим чуть позднее, а пока рассмотрим сложение и вычитание комплексных чисел.
Сложение и вычитание
Чтобы сложить комплексные числа, нужно сложить их действительные и мнимые части. Приведем такой пример:
Теперь сложим сопряженные числа из предыдущего подраздела:
Отсюда можно сделать вывод, что сумма сопряженных комплексных чисел равна удвоенной действительной части этих чисел. Чтобы вычесть одно комплексное число из другого, нужно заключить вычитаемое в скобки, а потом раскрыть их по всем правилам с изменением знака внутри на противоположный. Пример:
Еще пример:
Пример с сопряженными числами:
В результате получается чисто мнимое число. Теперь поменяем местами вычитаемое и уменьшаемое:
Получили противоположный результат. Как видим, для сложения и вычитания комплексных чисел достаточно раскрыть скобки и привести подобные слагаемые, как это делается с обычными многочленами. Далее рассмотрим умножение и деление комплексных чисел.
Умножение и деление
При умножении комплексных чисел пользуются известным правилом умножения многочленов: чтобы перемножить многочлены, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Но в процессе умножения не стоит забывать о второй степени мнимой единицы \((i^2 = -1)\). Приведем пример:
Теперь перемножим в общем виде сопряженные числа:
Получается, что произведение сопряженных комплексных чисел не содержит мнимой части, то есть является действительным и притом всегда положительным числом. Далее рассмотрим деление комплексных чисел. Найдем частное \((7-4i) : (3+2i)\). Запишем это выражение в виде дроби и расширим ее на сопряженное со знаменателем число \(3-2i\):
В результате такого расширения мы получим в знаменателе действительное число, на которое почленно разделим числитель:
Теперь настало время поговорить о других формах записи комплексных чисел.
Тригонометрическая и показательная форма комплексного числа
Тригонометрическая форма комплексного числа имеет следующий вид:
Обозначение \(|z|\) — это модуль комплексного числа, \(\varphi\) — его аргумент. Чтобы разобраться во всех этих модулях и аргументах, рассмотрим следующий рисунок:
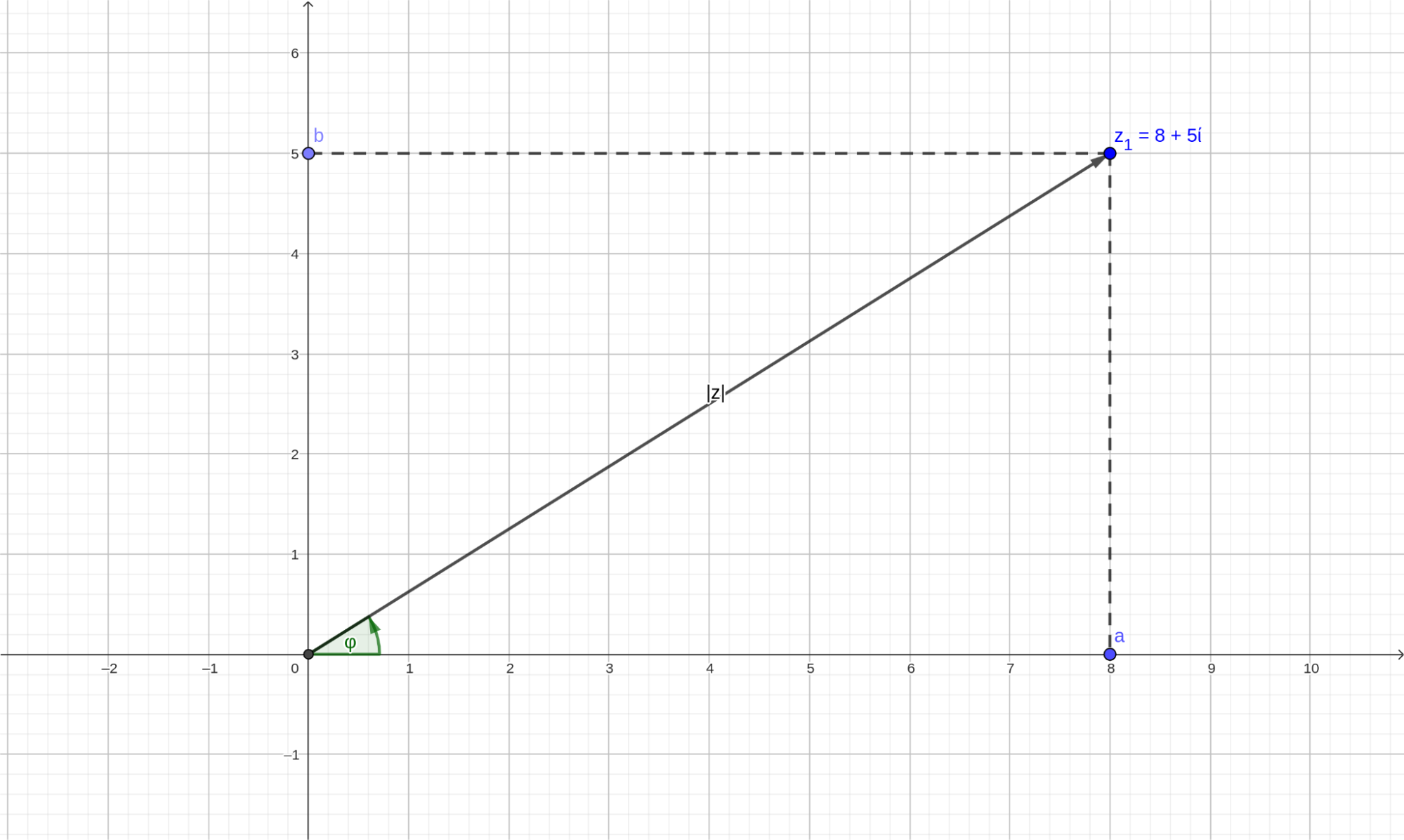
Как видим, модуль комплексного числа — это расстояние от начала координат до точки, представляющей комплексное число. То есть это длина вектора, который также является гипотенузой прямоугольного треугольника. А это значит, что модуль мы легко можем найти по теореме Пифагора:
Аргумент числа — это угол \(\varphi\) между действительной положительной полуосью и вектором, проложенным от начала координат до точки комплексного числа. Аргумент еще обозначают как \(arg z\). Так как действительная часть (a) и мнимая часть (b) комплексного числа — это катеты прямоугольного треугольника, то аргумент можно найти по такой формуле:
Но здесь еще следует учитывать то, в какой координатной четверти находится число. Вышеприведенная формула прекрасно работает только для правой полуплоскости (первая и четвертая четверти). Если число находится во второй четверти, то нужно применять эту формулу:
Если же число находится в третьей четверти, то формула будет уже такая:
Теперь представим в тригонометрической форме какое-нибудь число. Для примера возьмем число \(z = 1 — \sqrt{3i}\). Сначала найдем модуль:
Так как число находится в правой полуплоскости (a > 0), то аргумент вычисляется так:
Значит, тригонометрическая форма для данного числа будет иметь следующий вид:
Кроме тригонометрической формы, существует еще показательная. Общий вид у нее такой:
Как видим, здесь также нужны модуль и аргумент комплексного числа. Представим в показательной форме число из прошлого примера. Для этого просто подставим уже найденные значения модуля и аргумента в формулу:
Далее разберемся с тем, как возводить комплексные числа в степень.
Возведение в степень
Мы уже говорили о возведении в степень чисто мнимых чисел. Рассмотрим теперь возведение в степень комплексных чисел. Для примера возведем в квадрат число \(2+3i\). Мы можем просто умножить число само на себя по правилу умножения многочленов, а можем применить формулу сокращенного умножения (не забываем, что \(i^2= -1\)):
Но такой способ подходит для небольших степеней. А что делать, если понадобится возвести число в десятую, двадцатую или сотую степень? Здесь на помощь придет так называемая формула Муавра. Вот она:
И снова нам потребуются модули и аргументы. Возведем в тридцатую степень число \(1-\sqrt3i\). Модуль и аргумент для этого числа мы вычисляли в прошлом подразделе. Применим формулу Муавра:
Как видим, ничего особо сложного здесь нет.
Извлечение корня
Пусть требуется извлечь корень n-й степени из какого-либо комплексного числа w. Другими словами, нужно решить уравнение \(z = \sqrt[n]w\). Это уравнение имеет ровно n корней. Для их вычисления применяется такая формула:
В этой формуле k принимает значения от 0 до \(n − 1\), в зависимости от индекса корня. Так, для первого корня k = 0, для второго k = 1 и так далее. Теперь попробуем решить уравнение \(z^2=1+\sqrt3i\). Перепишем его в виде \(z=\sqrt{1+\sqrt3i}\). В этом уравнении n = 2, а \(w=1+\sqrt3i\). Параметр k может принимать значения 0 и 1, то есть уравнение будет иметь два корня \(z_0\) и \(z_1\). Сначала найдем модуль и аргумент комплексного числа w. Ищем модуль:
Так как число w находится в первой координатной четверти, то его аргумент вычислим так:
Теперь у нас есть все необходимые значения. Ищем первый корень:
Второй корень:
Теперь немного расскажем о применении комплексных чисел.
Где используют комплексные числа
Существуют еще так называемые гиперкомплексные числа. Такие числа имеют в своем составе несколько мнимых единиц. Если обычные комплексные числа можно представить как двумерные, которые можно изображать на плоскости, то гиперкомплексные числа могут быть изображены в евклидовых пространствах, имеющих три и более измерений. Из-за этого они очень удобны для моделирования и исследования пространственных объектов различной степени сложности.
Конечно, во многих случаях можно обойтись и без применения комплексных чисел, но в некоторых ситуациях они значительно упрощают ход вычислений. Поэтому эти числа широко применяются в создании компьютерной 2D-графики. В свою очередь гиперкомплексные числа отлично подходят для создания 3D-графики. Но только графикой не ограничивается применение комплексных чисел. Они также широко используются в исследовании колебательных процессов, магнитодинамике, некоторых областях экономики и во многом другом.








