Мы собрали 12 интересных математических задач и расписали их пошаговые решения. Среди них задачи на нахождение площади трапеции и треугольника, длину хорды, системы уравнений, прогрессии и построение графиков.
Площадь трапеции
Дана равнобедренная трапеция, у которой основания равны 8 и 20 см. Периметр трапеции равен 56 см. Требуется найти площадь трапеции.
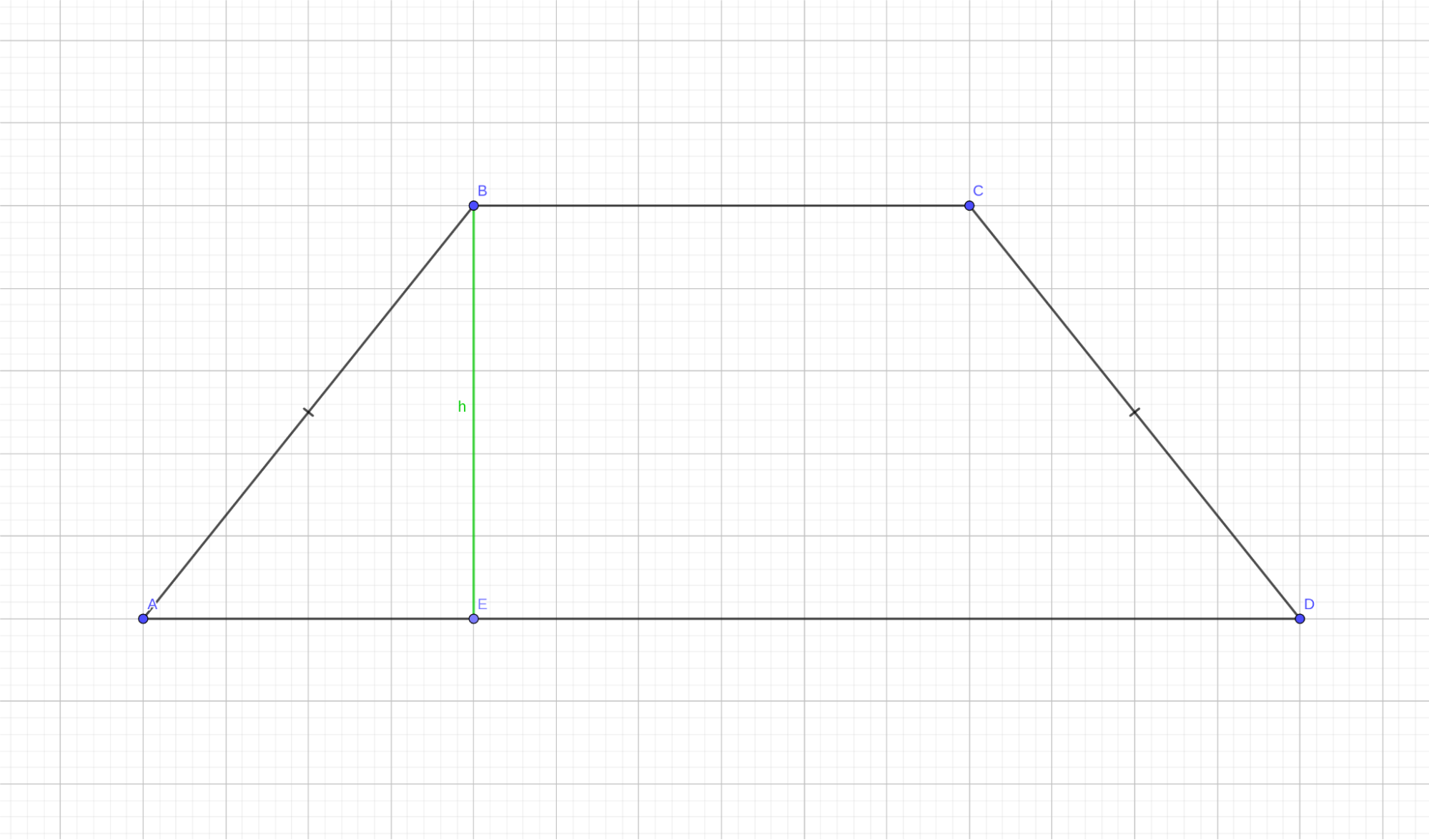
Как известно, площадь трапеции равна половине суммы оснований, умноженной на высоту. Исходя из чертежа, площадь трапеции будет вычисляться по следующей формуле:
\[ S = \frac{BC + AD}{2} \cdot BE \]
Из этой формулы нам неизвестна только высота трапеции BE.
Как нам ее найти? Посмотрим внимательно на чертеж. Высота трапеции является частью прямоугольного треугольника ABE, поэтому ее можно найти, используя теорему Пифагора. Так как высота — это один из катетов треугольника, нам осталось найти его второй катет AE и гипотенузу AB.
Найдем гипотенузу. Нам известен периметр трапеции, ее основания и то, что она равнобедренная. Из этого мы легко выведем такую формулу:
\[ AB = \frac{P — (BC + AD)}{2} \]
Действительно: периметр — это сумма всех сторон трапеции. Значит, если мы отнимем от периметра сумму оснований, то у нас останется только сумма боковых сторон. Так как трапеция равнобедренная, то боковые стороны у нее одинаковые, и достаточно разделить эту сумму пополам, чтобы получить одну боковую сторону.
Подставляем известные значения в формулу:
\[ AB = \frac{56 — (20 + 8)}{2} = \frac{28}{2} = 14 \]
Гипотенузу нашли. Теперь найдем катет AE. Здесь все просто. Нам снова поможет равнобедренность трапеции. Присмотримся внимательней к чертежу. Из чего можно составить нижнее основание? Оно как раз легко составляется из верхнего и двух одинаковых отрезков, каждый из которых равен искомому катету. Значит, найти этот катет можно, просто отняв из большего основания меньшее и поделив все на 2:
\[ AE = \frac{AD — BC}{2} = \frac{20 — 8}{2} = \frac{12}{2} = 6 \]
Итак, у нас есть все необходимые данные, чтобы найти высоту трапеции. Применяем теорему Пифагора:
\[ BE = \sqrt{AB^2 — AE^2} = \sqrt{14^2 — 6^2} = \sqrt{196 — 36} = \sqrt{160} = 4\sqrt{10} \]
Высота найдена. Подставляем все известные значения в формулу для нахождения площади:
\[ S = \frac{BC + AD}{2} \cdot BE = \frac{20 + 8}{2} \cdot 4\sqrt{10} = 14 \cdot 4\sqrt{10} = 56\sqrt{10} \]
Ответ: площадь трапеции равна \( 56\sqrt{10} \, \text{см}^2 \).
Длина хорды окружности
Дана окружность радиусом 15 см. Ее хорда находится на расстоянии 5 см от центра окружности. Требуется найти длину хорды.
Строим чертеж с учетом того, что расстояние от точки до отрезка отсчитывается по перпендикуляру:
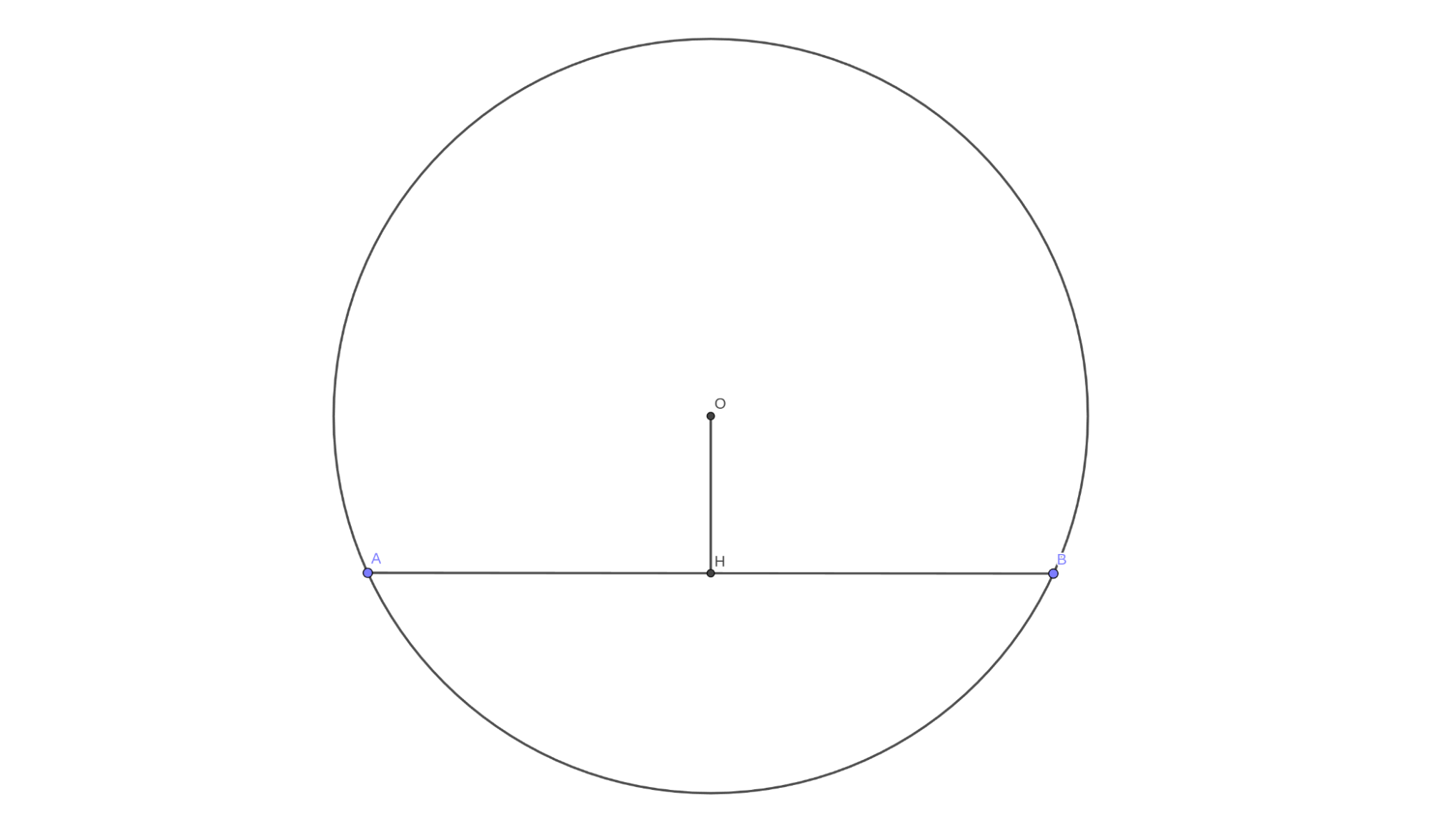
Нам нужно найти длину отрезка AB. Длина отрезка OH нам известна, также как и радиус. Достроим чертеж таким образом:
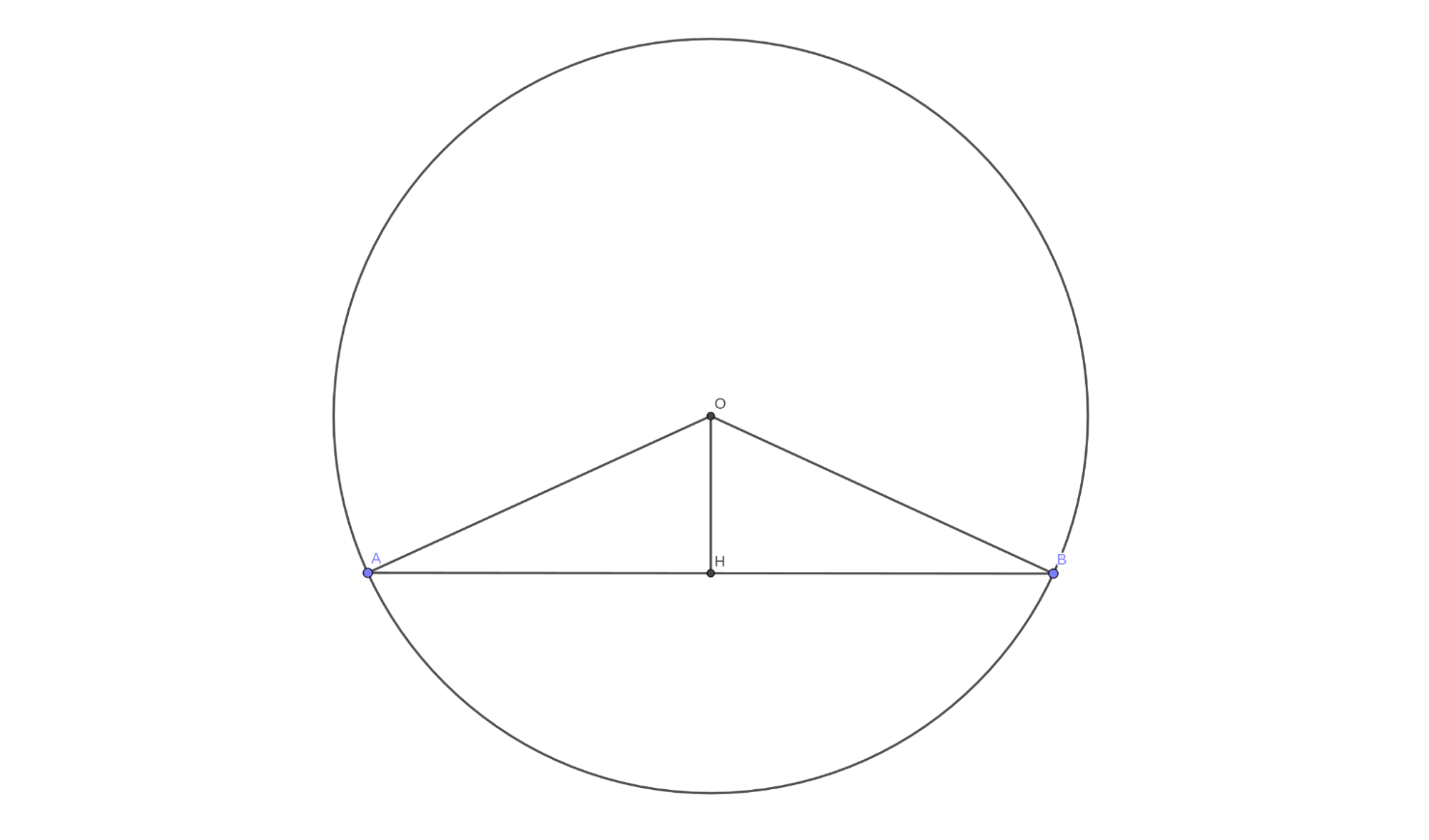
Сразу замечаем, что у нас получился равнобедренный треугольник, составленный из двух одинаковых прямоугольных треугольников. Учитывая, что AH = HB, достаточно найти только одну сторону прямоугольного треугольника, а потом умножить ее длину на 2. Гипотенуза AO — это радиус окружности, и он нам известен. И, как уже говорилось, катет OH нам тоже известен. Остается только воспользоваться теоремой Пифагора:
\[ AH = \sqrt{AO^2 — OH^2} = \sqrt{15^2 — 5^2} = \sqrt{225 — 25} = \sqrt{200} = 10\sqrt{2} \]
Так как \( AB = 2 \cdot AH \), то \( AB = 2 \cdot 10\sqrt{2} = 20\sqrt{2} \).
Ответ: длина хорды равна \( 20\sqrt{2} \, \text{см} \).
Площадь треугольника
Известно, что периметр равнобедренного треугольника равен 18, а его боковая сторона — 5. Нужно найти площадь этого треугольника.
Решим эту задачу двумя разными способами. Первый способ снова потребует от нас умение применять теорему Пифагора. Построим чертеж:
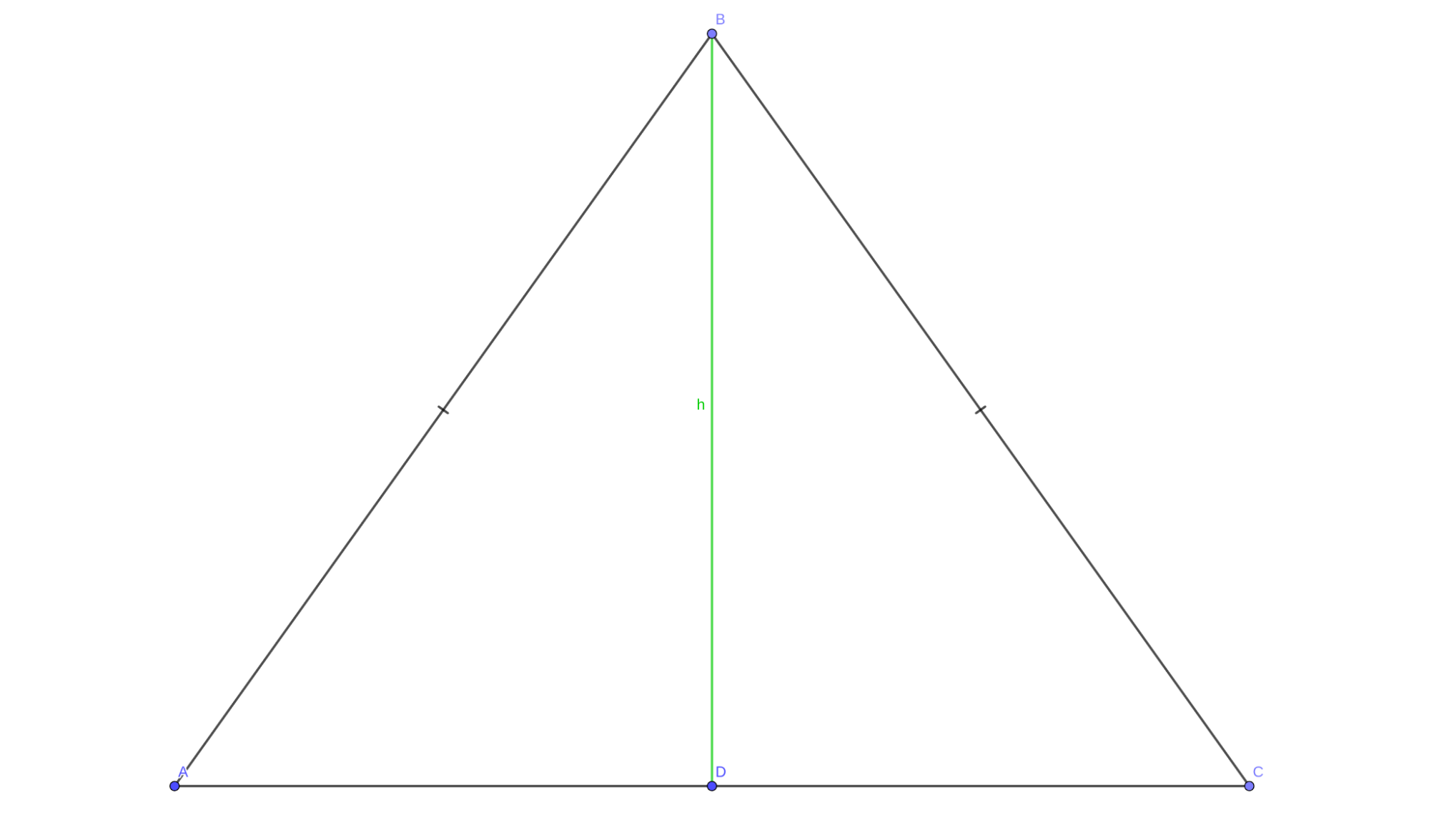
Мы провели высоту BD к основанию треугольника. Так как треугольник равнобедренный, то высота также является медианой и делит основание пополам. Периметр треугольника равен 18. В треугольнике имеются две равные боковые стороны, а значит, основание легко найти таким образом:
\[ AC = 18 — (2 \cdot 5) = 18 — 10 = 8 \]
Значит, сторона AD будет равна:
\[ AD = \frac{8}{2} = 4 \]
Так как треугольник ABD прямоугольный, то мы можем найти высоту BD, используя теорему Пифагора:
\[ BD = \sqrt{AB^2 — AD^2} = \sqrt{5^2 — 4^2} = \sqrt{25 — 16} = \sqrt{9} = 3 \]
Применяем формулу площади треугольника:
\[ S = \frac{AC \cdot BD}{2} = \frac{8 \cdot 3}{2} = \frac{24}{2} = 12 \]
Второй способ решения этой задачи заключается в использовании формулы Герона. Для этой формулы нужны все три стороны и полупериметр. У нас есть все данные, поэтому можно смело применять эту формулу:
\[
S = \sqrt{p(p — a)(p — b)(p — c)} = \sqrt{9 \cdot (9 — 5) \cdot (9 — 5) \cdot (9 — 8)} = \\
= \sqrt{9 \cdot 4 \cdot 4 \cdot 1} = 12
\]
Ответ: площадь треугольника равна 12.
Система уравнений
Решить систему уравнений:
\[
\begin{cases}
3x + y = 5 \\
\frac{x + 2}{2} + \frac{y}{4} = 1
\end{cases}
\]
Из первого уравнения выразим y через x. Оставим y в левой части, а слагаемое 3x перенесем в правую часть с переменой знака. Получим выражение:
\[y = 5 — 3x\]
Теперь правую часть полученного выражения подставим вместо y во второе уравнение системы. У нас получится такое уравнение с одной переменной:
\[\frac{x + 2}{2} + \frac{5 — 3x}{4} = 1\]
Перенесем 1 в левую часть, изменив знак на противоположный. Общим знаменателем для всех дробей будет число 4. Таким образом, для первого числителя дополнительный множитель — это 2, для второго — 1 и для третьего — 4. В итоге всех преобразований, в числителе получим следующее выражение:
\[2x + 4 + 5 — 3x — 4\]
Приводим подобные слагаемые и приравниваем получившееся выражение к нулю. В результате имеем простейшее линейное уравнение:
\[-x + 5 = 0\]
Решив его, получим x=5. Теперь мы легко найдем y:
\[y = 5 — 3 \cdot 5 = -10\]
Ответ: \( x = 5 \), \( y = -10 \).
Построение графика функции
Построить график функции
\[ f(x) = x^3 — 4x^2 + 3x \]
Функция определена при всех значениях x, то есть ее область определения — вся числовая прямая. Функция непрерывна, то есть не имеет точек разрыва. Определим точки пересечения графика функции с осью абсцисс. Для этого решим уравнение:
\[ x^3 — 4x^2 + 3x = 0 \]
Выносим x за скобку:
\[ x(x^2 — 4x + 3) = 0 \]
Сразу видим, что одним из корней данного уравнения будет нуль. Остальные корни — это корни квадратного уравнения:
\[ x^2 — 4x + 3 = 0 \]
Решив его, найдем два корня:
\[ x_1 = 1, \quad x_2 = 3 \]
Значит, точки пересечения графика с осью абсцисс — это точки с координатами A(0, 0), B(1, 0) и C(3, 0). Эти точки разбивают ось абсцисс на четыре промежутка знакопостоянства функции. На промежутке от нуля до единицы график должен находиться выше оси абсцисс, а на промежутке от 1 до 3 — ниже. Это легко проверить, если подставить в формулу функции какие-нибудь числа из этих промежутков. Соответственно, на промежутке от нуля до единицы должна находиться точка максимума, а на промежутке от 1 до 3 — точка минимума.
Найдем точки максимума и минимума функции. Для этого сначала вычислим производную:
\[ f'(x) = (x^3 — 4x^2 + 3x)’ = 3x^2 — 8x + 3 \]
Приравняв производную к нулю и решив получившееся квадратное уравнение, мы найдем два корня:
\[ x_1 \approx 0.46, \quad x_2 = 2 \]
Значит, x1 — это точка максимума, а x2 — точка минимума. Найдем значения функции в этих точках:
\[ f(0.46) \approx 0.46^3 — 4 \cdot 0.46^2 + 3 \cdot 0.46 \approx 0.06 \]
\[ f(2) = 2^3 — 4 \cdot 2^2 + 3 \cdot 2 = 8 — 16 + 6 = -2 \]
Итак, у нас есть пять контрольных точек: A(0, 0), B(1, 0), C(3, 0), D(0,46; 0,6), E(2,2; −2,1). Построив по этим точкам график, мы получим примерно следующее:
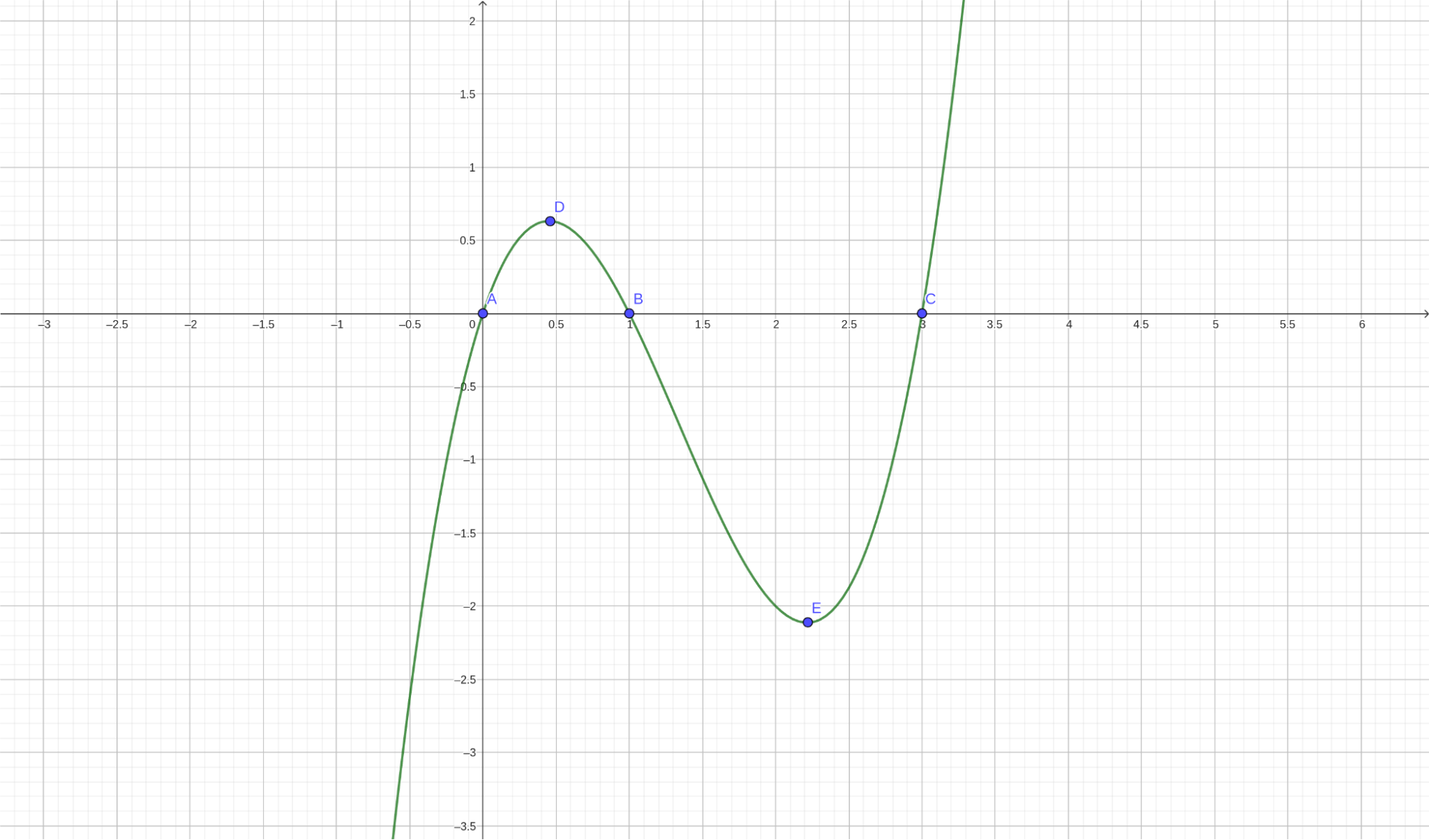
График функции построен.
Прогрессии
Выяснить, является ли число −122 членом следующей арифметической прогрессии:
23; 17,2; 11,4; 5,6; … .
В представленной прогрессии первый член \( x_1 = 23 \), а разность \( d = x_2 — x_1 = 17.2 — 23 = -5.8 \)
Значит, формула для нахождения n-го члена прогрессии будет иметь следующий вид:
\[x_n = 23 — 5.8(n — 1)\]
Или:
\[x_n = 28.8 — 5.8n\]
Для того чтобы узнать, является ли число −122 членом данной арифметической прогрессии, нужно решить уравнение:
\[28.8 — 5.8n = -122\]
Решаем его:
\[5.8n = 150.8, \quad n = 26\]
Это значит, что число −122 является 26-м членом арифметической прогрессии.
Решим еще одну задачу, но теперь уже про геометрическую прогрессию.
Найти восьмой член геометрической прогрессии, если известно, что \( b_1 = 162 \) и \( b_3 = 18. \)
Нам известны первый и третий члены геометрической прогрессии. Чтобы найти восьмой член прогрессии, необходимо узнать ее знаменатель.
Так как \( b_3 = b_1 q^2 \), то
\[q^2 = \frac{b_3}{b_1} = \frac{18}{162} = \frac{1}{9}.\]
Решив уравнение:
\[ q^2 = \frac{1}{9}, \]
обнаружим, что оно имеет два корня \( \frac{1}{3} \) и \( -\frac{1}{3} \).
Это значит, что существуют две прогрессии, удовлетворяющие условию задачи.
Если \( q = \frac{1}{3} \), то:
\[
b_8 = b_1 q^7 = 162 \cdot \left( \frac{1}{3} \right)^7 = \frac{2 \cdot 3^4}{3^7} = \frac{2}{27}
\]
Если \( q = -\frac{1}{3} \), то:
\[
b_8 = b_1 q^7 = 162 \cdot \left( -\frac{1}{3} \right)^7 = -\frac{2 \cdot 3^4}{3^7} = -\frac{2}{27}
\]
Ответ: \( b_8 = \frac{2}{27} \) и \( b_8 = -\frac{2}{27} \).
Тригонометрия
Доказать тождество:
\[
tg^2 \alpha — sin^2 \alpha = tg^2 \alpha sin^2 \alpha
\]
Произведем преобразование левой части равенства:
\[
tg^2 \alpha — sin^2 \alpha = \frac{sin^2 \alpha}{cos^2 \alpha} — sin^2 \alpha = sin^2 \alpha \left( \frac{1}{cos^2 \alpha} — 1 \right) = \\
= sin^2 \alpha \left( 1 + tg^2 \alpha — 1 \right) = tg^2 \alpha sin^2 \alpha
\]
Мы получили выражение, находящееся в правой части равенства, а это значит, что тождество доказано.
Решим еще одну задачу.
Требуется упростить следующее выражение:
\[
ctg^2 \alpha (cos^2 \alpha — 1)
\]
Для упрощения воспользуемся тем, что котангенс определяется как отношение косинуса к синусу, и тем, что сумма квадратов синуса и косинуса равна единице. Получим:
\[
ctg^2 \alpha (cos^2 \alpha — 1) = \frac{cos^2 \alpha}{sin^2 \alpha} (-sin^2 \alpha) = -cos^2 \alpha
\]
Выражение упрощено.
Решить уравнение:
\[
\text{tg}\, t = \sqrt{3}
\]
Неизвестное можно легко найти через арктангенс:
\[
t = \text{arctg} \, \sqrt{3} + \pi k, \, k \in \mathbb{Z}
\]
Осталось только вычислить \( \text{arctg} \, \sqrt{3} \). Для вычисления этого арктангенса нужно понимать, что это такое число, тангенс которого равен \( \sqrt{3} \) и которое принадлежит интервалу от \( -\frac{\pi}{2} \) до \( \frac{\pi}{2} \).
Получается, что \( \text{arctg} \, \sqrt{3} = \frac{\pi}{3} \).
Значит, корень уравнения будет иметь следующий вид:
\[
t = \frac{\pi}{3} + \pi k, \, k \in \mathbb{Z}
\]
Уравнение решено.
Текстовая задача
От причала по течению реки отправился плот. Вслед за плотом, от того же причала, через 5 ч 20 мин отправился катер. Через 20 км катер догоняет плот. Требуется узнать скорость плота, если известно, что собственная скорость катера больше скорости плота на 9 км/ч.
Обозначим собственную скорость катера (скорость в стоячей воде) через \( v_k \), а скорость течения реки — через \( v_p \). В условии задачи сказано, что собственная скорость катера больше скорости плота на 9 км/ч.
Значит, мы можем написать:
\[ v_k — v_p = 9 \]
Катер, двигаясь по течению реки, прошел 20 км за время \( \frac{20}{v_p} \), а плот прошел те же 20 км за время \( \frac{20}{v_k + v_p} \). Так как время, за которое плот прошел 20 км, на 5 ч 20 мин (16/3 ч) больше времени, за которое то же расстояние прошел катер, то составляем следующее уравнение:
\[
\frac{20}{v_p} — \frac{20}{v_k + v_p} = \frac{16}{3}
\]
Исходя из того, что \( v_k = v_p + 9 \), приводим уравнение к такому виду:
\[
\frac{20}{v_p} — \frac{20}{2v_p + 9} = \frac{16}{3}
\]
Получили уравнение с одной переменной, которое путем элементарных преобразований сводится к квадратному уравнению:
\[8v_p^2 + 21v_p — 135 = 0\]
Решив это уравнение, найдем два его корня \( v_p = 3 \) и \( v_p = -\frac{45}{8} \). По смыслу задачи подходит только первый корень. Следовательно, скорость течения реки, а значит, и скорость плота равна 3 км/ч.
Ответ: скорость плота равна 3 км/ч.
Доказательство неравенств
Доказать, что при любых значениях a верно неравенство
\[(a — 3)(a — 5) < (a - 4)^2\]
Из левой и правой частей неравенства составляем разность, то есть, по сути, просто переносим квадрат разности из правой части в левую с переменой знака:
\[(a — 3)(a — 5) — (a — 4)^2 < 0\]
И далее производим простейшие преобразования в левой части неравенства:
\[(a — 3)(a — 5) — (a — 4)^2 = a^2 — 3a — 5a + 15 — a^2 + 8a — 16 = -1\]
У нас получилось, что при любом значении переменной рассматриваемая разность отрицательна, а значит, при любом a верно исходное неравенство.
Докажем еще одно неравенство.
Доказать, что сумма квадратов любых двух чисел не меньше их удвоенного произведения.
Если a и b — произвольные числа, то нам нужно доказать следующее неравенство:
\[a^2 + b^2 \geq 2ab\]
Так же, как и в прошлом примере, составляем разность и проводим простейшие преобразования:
\[a^2 + b^2 — 2ab = a^2 — 2ab + b^2 = (a — b)^2\]
Мы получили квадрат разности двух переменных, а он всегда больше или равен нулю при любых значениях этих переменных. Значит, исходное неравенство верно при любых значениях a и b.
Простейшие показательные и логарифмические уравнения
Решить уравнение:
\[16^x = 512\]
Представим 16 в виде степени \( 2^4 \), а 512 в виде степени \( 2^9 \). Тогда неизвестное можно найти таким способом:
\[
x = \log_{16}{512} = \frac{\log_{2}{512}}{\log_{2}{16}} = \frac{\log_{2}{2^9}}{\log_{2}{2^4}} = \frac{9}{4}
\]
Но можно решить уравнение и более простым способом. Представим его в таком виде:
\[
\left( 2^4 \right)^x = 2^9
\]
Или:
\[2^{4x} = 2^9\]
Отсюда следует, что нам нужно решить простейшее линейное уравнение:
\[4x = 9\]
Решив его, найдем, что
\[x = \frac{9}{4}\]
Ответ: \( x = \frac{9}{4} \)
Решить уравнение:
\[\log_{\frac{1}{7}}{x} = -\frac{3}{4}\]
Корень находится следующим образом:
\[
x = \left( \frac{1}{7} \right)^{-\frac{3}{4}} = 7^{\frac{3}{4}} = \sqrt[4]{7^3} = \sqrt[4]{343}
\]
Ответ: \( x = \sqrt[4]{343} \)
Производная и высота конуса
Вычислить производную функции:
\[2x^3 — 4x^2 + 5x + 8\]
Найдем производные для каждого из слагаемых и сложим их. Для вычисления производных слагаемых воспользуемся следующей формулой:
\[
\left( x^n \right)’ = n x^{n-1}
\]
Не забываем, что производная постоянной равна нулю. Получим:
\[
\left( 2x^3 — 4x^2 + 5x + 8 \right)’ = 6x^2 — 8x + 5
\]
Решим еще одну задачу.
Требуется найти высоту конуса наибольшего объема, если известно, что его образующая равна l.
Если известна площадь основания конуса S и его высота H, то объем этого конуса можно вычислить по такой формуле:
\[V = \frac{1}{3} S H\]
В условии задачи образующая конуса указана как постоянная величина, а высота конуса должна быть переменной. Нам нужно сделать так, чтобы в формуле были только l и H. Для этого выразим площадь основания конуса через радиус окружности, которая лежит в основании конуса:
\[S = \pi R^2\]
По теореме Пифагора радиус основания, высота конуса и его образующая будут связаны таким равенством:
\[l^2 = R^2 + H^2\]
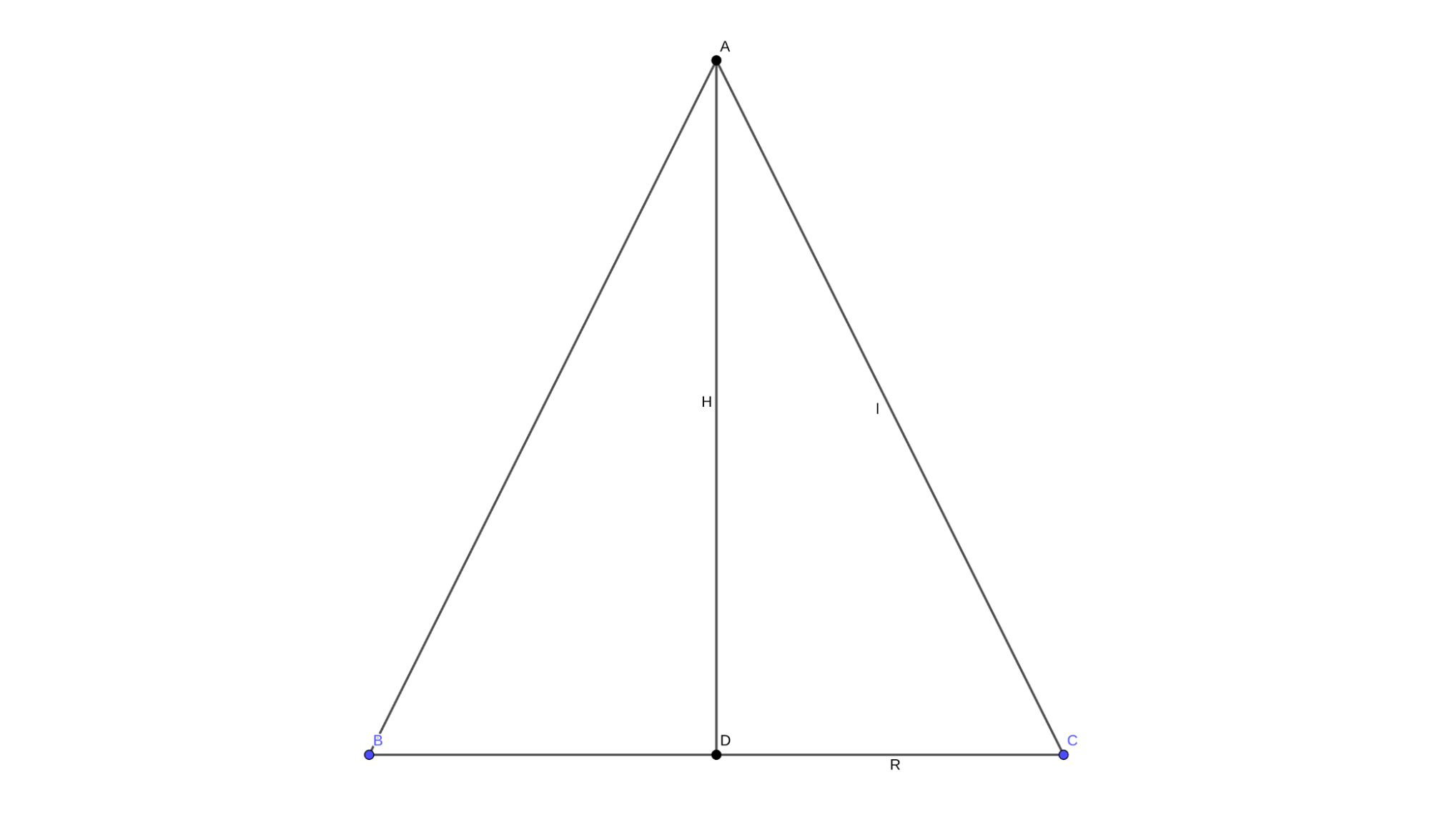
Воспользовавшись этим равенством, мы теперь можем выразить объем конуса V как функцию только от одной переменной H:
\[V(H) = \frac{1}{3}\pi(l^2 — H^2)H\]
Теперь вычислим производную этой функции и приравняем ее к нулю. У нас получится следующее уравнение:
\[\frac{\pi}{3}(l^2 — 3H^2) = 0\]
Решив это уравнение, мы получим две критические точки: \( H_1 = \frac{l}{\sqrt{3}} \) и \( H_2 = -\frac{l}{\sqrt{3}} \). Промежутку от нуля до \( l \) принадлежит только точка \( H_1 \). При переходе через эту точку производная меняет знак с плюса на минус, а это значит, что \( H_1 \) — точка максимума. Следовательно, высота конуса наибольшего объема при заданной длине образующей \( l \) равна \( \frac{l}{\sqrt{3}} \).
Ответ: \( H = \frac{l}{\sqrt{3}} \).
Первообразная и площадь криволинейной трапеции
Найти все первообразные для следующего многочлена:
\[5x^3 — 4x + 3\]
Найдем первообразные для каждого из слагаемых и сложим их. Для вычисления первообразных слагаемых воспользуемся тем, что первообразная степенной функции \(x^{\alpha}\) (\(\alpha \neq -1\)) равна \(\frac{x^{\alpha+1}}{\alpha+1}\). В итоге получим следующий многочлен:
\[\frac{5x^4}{4} — 2x^2 + 3x\]
Это только одна из первообразных. Все первообразные для исходного многочлена будут иметь вид:
\[\frac{5x^4}{4} — 2x^2 + 3x + C, \, \text{где} \, C \, \text{— любая постоянная.}\]
Решим еще одну задачу.
Требуется вычислить площадь криволинейной трапеции, которая сверху ограничена графиком функции \(x^2 + 1\), снизу осью абсцисс, а с боков прямыми \(x = 1\) и \(x = 4\).
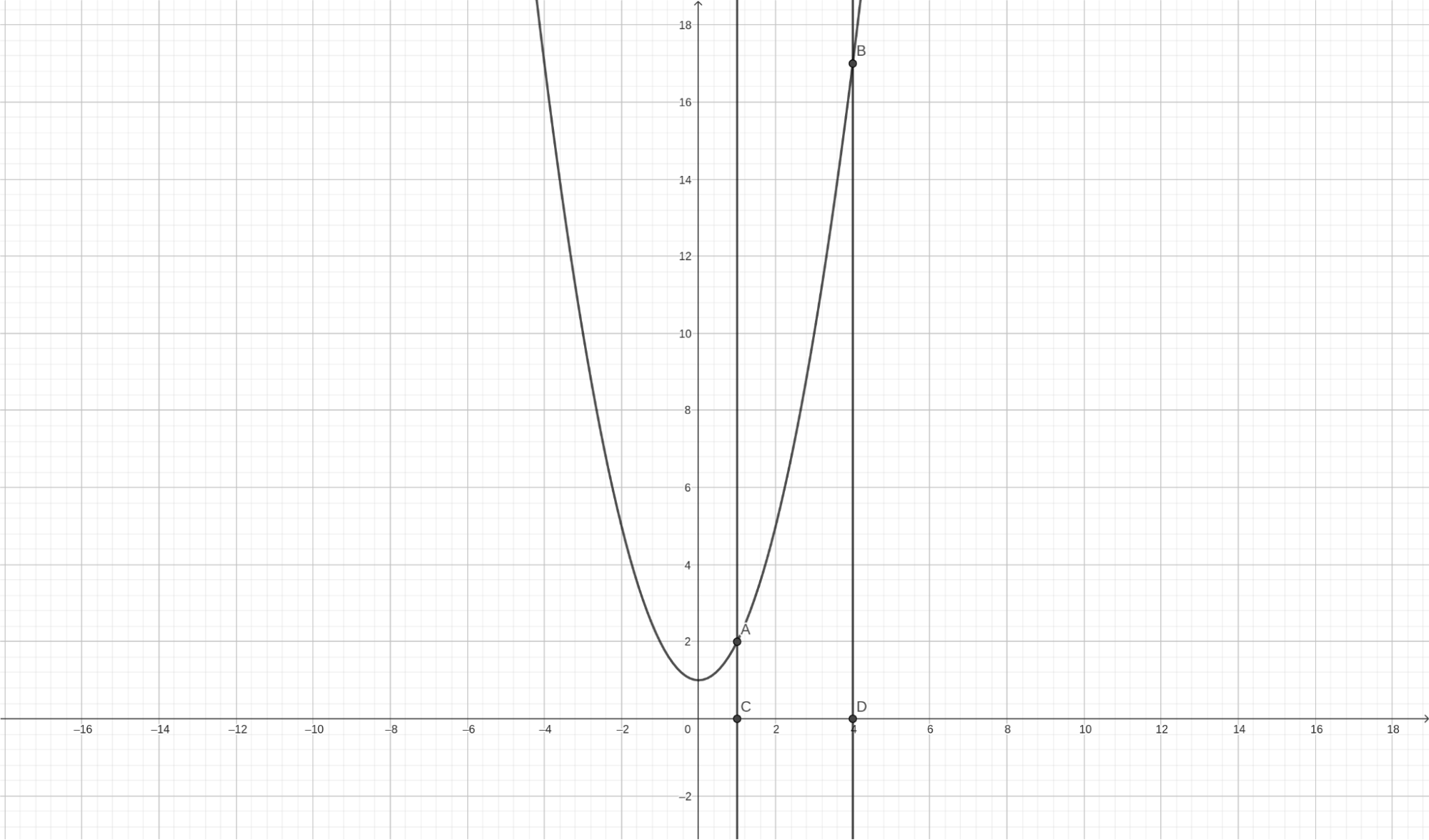
Для вычисления площади криволинейной трапеции нам потребуется вычислить интеграл:
\[ S = \int\limits_1^4 \left( x^2 + 1 \right) dx \]
Одна из первообразных функции \(x^2 + 1\) равна \( \frac{x^3}{3} + x \), а значит,
\[ S = \left( \frac{4^3}{3} + 4 \right) — \left( \frac{1^3}{3} + 1 \right) = 24. \]
Ответ: \( S = 24 \).