Можно заниматься машинным обучением без владения математическим аппаратом — используйте готовые библиотеки, находите в интернете нужные алгоритмы под каждую задачу, применяйте их к данным. Однако, чтобы стать профессионалом, нужно понимать принципы, которые стоят за этими инструментами. Рассказываем о необходимой базе владения линейной алгеброй.
Линейная алгебра применяется для решения всех основных задач Data Science: создания и настройки моделей, тренировки нейросетей и применения аналитических систем к информации. Программы машинного обучения фактически и представляют собой линейные функции, которым вы «скармливаете» данные, чтобы получить результат. Этот процесс работает в обе стороны — вы можете по результату восстановить исходный материал, как в обучении без учителя, или формировать прогнозы на будущее.
Если у вас стоит задача определить взаимосвязь двух явлений, вы применяете линейную регрессию. Когда некие данные нужно распределить по классам, вам помогает регрессия логистическая. Методы главных компонент (Principal Component Analysis) и опорных векторов (Support-Vector Machine), функции регуляризации, градиентный спуск — все эти инструменты помогают дата-сайентистам в их ежедневной работе.
Рассмотрим десять методов линейной алгебры, которые чаще всего применяют специалисты по машинному обучению и нейросетям. Всех желающих лучше разобраться в этой теме, повысить свои компетенции и привлекательность для работодателей приглашаем на наш курс по математике для Data Science.
Функции потерь (Loss Functions)
Для большинства именно с этого начинается знакомство с Data Science — функции потерь помогают создавать рекомендательные и прогнозные системы, определять тенденции в массивах данных.
Допустим, у вас есть модель линейной регрессии, которой вы предлагаете исходные данные. Полученный результат вы сравниваете с образцом, чтобы определить, как далеко от реальности он лежит. Эта информация помогает вам оптимизировать функцию прогнозирования.
Как же подсчитать эту разницу? Для этого вы представляете эти данные в виде двух векторов и применяете к ним функцию потерь. Например, пусть ожидаемый прогноз — это вектор P, а ваши результаты — вектор E. Тогда P-E — это разница между данными, а длина этого третьего вектора и представляет собой величину ошибки.
Регуляризация (Regularization)
При создании аналитических моделей следует избегать двух крайностей — недообучения (underfitting) и переобучения (overfitting), В первом случае алгоритм делает поспешные выводы, во втором строит функцию слишком близко к исходным данным. Истина лежит посередине, и достичь ее помогает регуляризация.
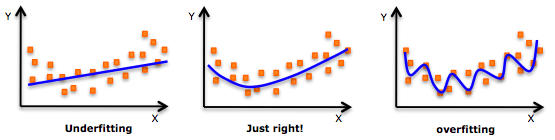
Для этого к целевой функции добавляются весовые коэффициенты. Они не позволяют функции «отвлекаться» на избыточные данные, обеспечивая нужный результат.
Ковариантная матрица (Covariance Matrix)
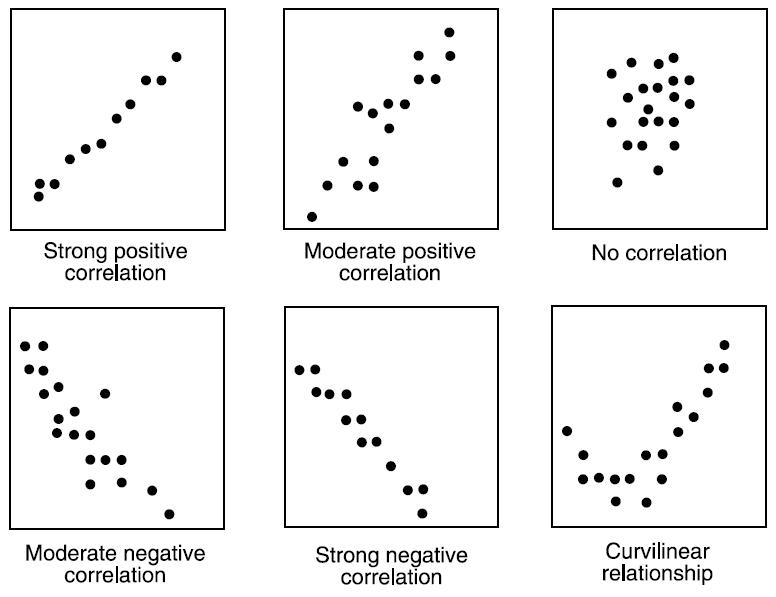
Бивариантный анализ позволяет изучать взаимосвязи между парами переменных. Ковариантность, которая применяется в такой работе, помогает определить линейное направление изменений в таких моделях. Позитивная ковариантность означает, что увеличение или уменьшение одной переменной приводит к симметричному изменению другой. Отрицательная ковариантность свидетельствует об обратном изменении — увеличение одного параметра уменьшает второй, и наоборот.
Определяя значение ковариантности, мы получаем показатель корреляции, который лежит в пределах от -1 до 1. Он объединяет в себе величину и направление линейной взаимосвязи двух переменных.
Метод опорных векторов (Support-Vector Machine)
Как говорилось выше, техника SVM применяется для классификации объектов. Для этого используется концепция векторных пространств — математических структур, объединяющих множество векторов, с которым можно проводить операции сложения, вычитания и умножения.
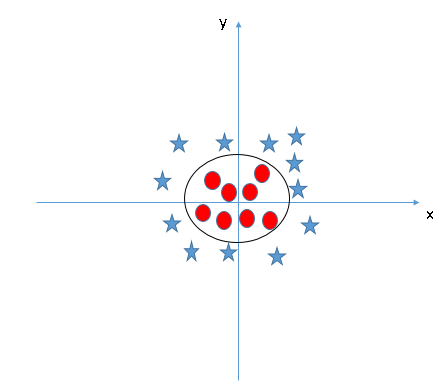
Для решения этой задачи каждая переменная (фактически, каждый объект, который нужно отнести к тому или иному классу) выражается в виде точки в n-мерном пространстве, где n — это количество характеристик, которыми вы располагаете. Координаты каждой точки обозначают соответствующие характеристики. Далее алгоритм с помощью метода опорных векторов находит гиперплоскость, которая пролегает точно между группами наших объектов.
Поскольку таких гиперплоскостей может быть больше одной, необходимо определить такую, которая пролегает на максимально далеком расстоянии от каждого объекта. Очевидно, это обеспечивает наилучшую классификацию.
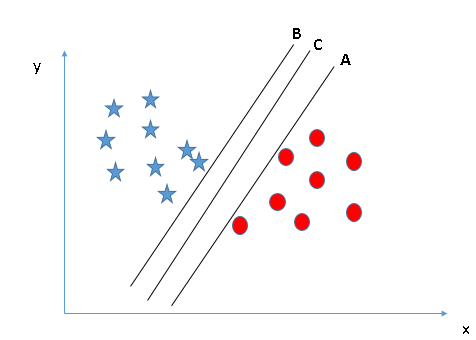
Метод работает и в том случае, если объекты распределяются иным образом, например, одна группа кольцом окружает другую. Дата-сайентист преобразует одно пространство в другое, с которым далее можно проводить операции.
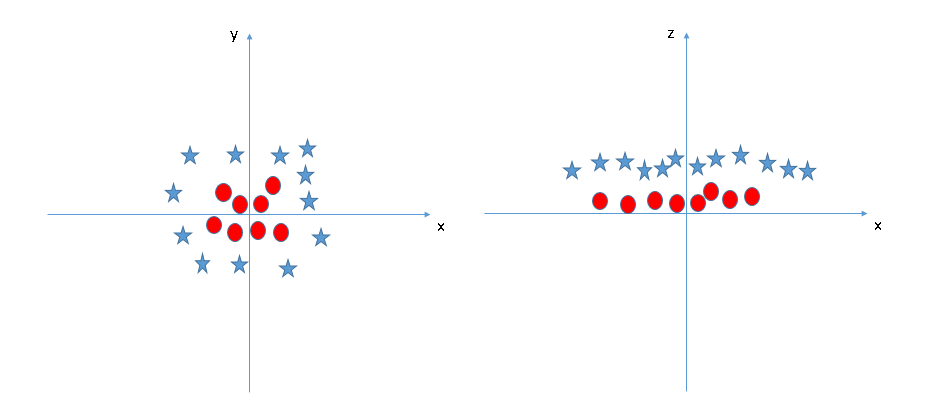
Метод главных компонент (Principal Component Analysis, PCA)
Очень часто эксперту по Data Science приходится работать с наборами данных, которые включают сотни и тысячи переменных. Большинство из них не представляют практического смысла, но даже если отсеять 99 мусорных процентов, на анализ оставшихся данных может потребоваться слишком много времени и ресурсов.
В таких случаях используются техники уменьшения размерности (dimensionality reduction), которые определяют переменные, сильнее всего влияющие на результат. Один из наиболее применимых методов для решения таких задач — метод главных компонент. Если не углубляться в математику, достаточно сказать, что таким образом можно найти основные векторы и спроецировать остальные данные согласно им. Если хотите узнать подробнее, почитайте о вычислении собственных векторов и собственных значений ковариационной матрицы.
Сингулярное разложение (Singular Value Decomposition)
Еще один способ понизить размерность без потери значительной доли ценной информации. Если у вас есть исходная матрица с большим объемом данных, вы можете разложить ее на меньшие матрицы, которые будут обладать теми же свойствами. Это отличный способ получить полезный результат в шумных условиях или в тех случаях, когда информации, напротив, не хватает.
Например, Netflix применяет SVD в своих рекомендательных системах, где объем исходной информации (количество фильмов в базе) несравнимо превышает объем информации рабочей (количество фильмов, которые посмотрел пользователь). Кроме того, таким образом оказывается удобно обрабатывать изображения и музыку, сжимая их с минимальным ущербом качеству.
Векторное представление слов (Word Embeddings)
Как нетрудно догадаться, этот метод используется для работы с текстом в NLP-системах (Natural Language Processing). Компьютеры не понимают человеческий язык, хотя в последнее время им и удается более-менее успешно производить обратное впечатление. Это становится возможным благодаря техникам «цифровизации» слов, которые переводят их семантическое значение в векторы.
Для этого используются самые разные атрибуты — количество букв в слове, теги обозначения частей речи и грамматических отношений между ними, векторные нотации и многое другое. Эти данные помещаются в n-мерное пространство, где аналитическая модель определяет между ними взаимосвязи, выстраивает контекстные цепочки и так далее.
Таким образом нейросеть может переварить некий языковой корпус и строить на его основе предложения. Собственных мыслей к компьютера нет, так что от своего лица он может только нести грамматически верную чушь. А понимать поступающие реплики и формировать ответы на них таким образом получается очень хорошо.
Латентный семантический анализ (Latent Semantic Analysis, LSA)
Когда вы читаете предложение «Я увидел каменный замок, на его воротах висел замок», вы легко распознаете значения двух омонимов. Аналогично, вам несложно подобрать синоним к какому-либо слову — вы понимаете его значение и представляете, чем можно его заменить. Однако компьютеру такие операции даются с трудом, и создателям NLP-продуктов приходится придумывать, как обеспечить их системе возможность понимать контекст.
В этом им снова помогает алгоритм сингулярного разложения. Они разбивают некий объем текстовых материалов на меньшие матрицы, по которым можно соотнести тему, ее контекст и употребляемые термины. Такое разложение помогает найти внутренние связи в массивном наборе текстов и понимать контекстуальное значение слов.
Тензоры и работа с изображениями
Вектор — это простой массив данных, матрица — двухмерный массив, а тензор объединяет n измерений, где n>2. Компьютерные системы используют эти структуры, чтобы видеть и понимать изображения.
Для передачи цвета в цифровых изображениях используется шкала RGB — Red, Green, Blue. Когда аналитическая модель получает некую картинку, она создает тензор, который объединяет в себе три матрицы, у которых в каждой ячейке хранится цветовое значение соответствующего пикселя. Первая такая матрица содержит значения красного, вторая — зеленого, третья — синего. Пример того, как дальше можно работать с этими данными в следующем пункте.
Функция свертки
Напоследок рассмотрим функцию свертки, которая позволяет определять объекты на изображениях. Механика, в общем-то, напоминает работу человеческого мозга — модель запоминает некий образ, а потом внимательно рассматривает предложенную картинку, чтобы найти его среди пикселей.
Для компьютера такой образ представляет собой сумму значений пикселей, которые составляют изображение целевого объекта. Эта сумма называется ядром. Имея в своем распоряжении такое ядро, программа поочередно сравнивает его с разными участками изображения. В том участке, где совпадение оказывается максимальным, она и предполагает наличие искомого объекта.
Этот механизм также можно использовать, чтобы повысить или понизить четкость изображений, наложить на него разнообразные фильтры. Принцип один и тот же — когда нейросеть распознает определенные объекты, она может проводить с ним требуемые операции.







