Разбираемся, что такое НОК и НОД и какими способами их можно найти — самостоятельно и с помощью специальных сервисов. А еще — решаем несколько задач с помощью НОК и НОД.
Что такое НОК и НОД чисел
НОК — это наименьшее общее кратное двух и более чисел.
Общее кратное — число, которое можно разделить без остатка на любое из представленных чисел. Например, если взять 15, 6 и 10, то общее кратное будет равно 180. При этом 90 — тоже общее кратное для этих чисел. Среди всех общих кратных всегда есть наименьшее, в данном случае число 30. Это и есть НОК.
НОД — это наибольший общий делитель. То есть наибольшее число, на которое два или более чисел могут делиться без остатка. Например, числа 12, 18 и 30 имеют общий делитель 3, но 2 — тоже их общий делитель. Наибольшее по значению число будет считаться НОД. В нашем случае — число 6.
В первую очередь НОК и НОД чисел используют для математических вычислений. К примеру, работы с дробями — упрощения, приведения к общему знаменателю.
Кроме этого, они применяются в таких дисциплинах, как теория чисел, компьютерные науки, инженерия и даже криптография. В некоторых алгоритмах шифрования используется НОД для определения взаимной простоты чисел — когда два и более числа не имеют общих делителей, кроме числа 1. Это помогает однозначно расшифровывать сообщения, что критически важно для безопасности всей системы.
Как найти НОД чисел
Рассмотрим два несложных способа нахождения НОД: метод разложения на простые множители и алгоритм Евклида.
Разложение на простые множители
Задача решается в два этапа. Сначала нужно разложить каждое число на простые множители. А затем — найти общие множители и возвести их в наименьшую степень, в которой они присутствуют в разложении чисел.
Пример: найти НОД для чисел 252, 441 и 1080.
Разложим каждое из них на простые множители:
\(252 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
\(441 = 3 \cdot 3 \cdot 7 \cdot 7\)
\(1080 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5\)
Возведем множители в степень:
\(252 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7 = 2^2 \cdot 3^2 \cdot 7\)
\(441 = 3 \cdot 3 \cdot 7 \cdot 7 = 3^2 \cdot 7^2\)
\(1080 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5 = 2^3 \cdot 3^3 \cdot 5\)
Общий множитель для чисел — 3, а наименьший из показателей степени, с которыми множитель 3 входит в данные числа, — 2. Значит, НОД = 32 = 9.
Другой пример: найдем НОД для чисел 234, 1080 и 8100.
Разложим на множители:
\(234 = 2 \cdot 3 \cdot 3 \cdot 13\)
\(1080 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5\)
\(8100 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 5 \cdot 5\)
Возведем множители в степень:
\(234 = 2 \cdot 3 \cdot 3 \cdot 13 = 2 \cdot 3^2 \cdot 13\)
\(1080 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5 = 2^3 \cdot 3^3 \cdot 5\)
\(8100 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 5 \cdot 5 = 2^2 \cdot 3^4 \cdot 5^2\)
Здесь общие множители 2 и 3. Двойка входит в указанные числа с наименьшим показателем, равным единице, а у тройки наименьший показатель равен двум. Значит, НОД = 232 = 18.
Если у чисел нет общего множителя, НОД считается равным единице.
Пример: найти НОД для чисел 15, 10 и 6.
Разложим на множители:
\(15 = 3 \cdot 5\)
\(10 = 2\cdot 5\)
\(6 = 2 \cdot 3 \)
Как видим, множителей, общих для всех трех чисел, здесь нет. Поэтому НОД = 1.
Алгоритм Евклида
Этот алгоритм помогает найти НОД двух целых чисел. Он назван в честь древнегреческого математика Евклида, который впервые описал алгоритм в своем труде «Начала».
Есть две разновидности этого алгоритма: первая позволяет находить НОД пары чисел с помощью деления, а вторая — вычитания.
Алгоритм вычисления НОД при помощи деления:
- Сначала большее из двух чисел делим на меньшее.
- Если деление произошло без остатка, то меньшее из чисел и есть НОД.
- Если имеется остаток, то большее из чисел заменяем на этот остаток.
- Переходим к первому пункту.
Пример: вычислим НОД чисел 30 и 18.
\(30 \div 18 = 1 \text{ (и в остатке } 12\text{)}\)
\(18 \div 12 = 1 \text{ (и в остатке } 6\text{)}\)
\(12 \div 6 = 2 \text{ (без остатка)}\)
Значит, НОД = 6.
Алгоритм вычисления НОД с помощью вычитания:
- Сначала вычитаем из большего числа меньшее.
- Если получаем нуль, то числа равны друг другу и являются НОД.
- Если результат отличен от нуля, то большее число заменяем на результат вычитания.
- Возвращаемся к первому пункту, пока не получим нуль.
Пример: возьмем те же числа — 30 и 18.
\(30 — 18 = 12 \text{ (больше нуля, заменяем большее число на } 12\text{)}\)
\(18 — 12 = 6 \text{ (больше нуля, заменяем большее число на } 6\text{)}\)
\(12 — 6 = 6 \text{ (больше нуля, заменяем большее число на } 6\text{)}\)
\(6 — 6 = 0\)
Значит, НОД = 6.
Как найти НОК чисел
Для вычисления НОК можно применить способ разложения на множители, который мы разобрали выше. Либо найти НОК через НОД.
Рассмотрим оба способа.
Разложение на множители
Алгоритм действий включает следующие шаги:
- Сначала нужно разложить все числа на простые множители.
- Потом выписать все простые множители, входящие хотя бы в одно из чисел.
- Каждый из взятых множителей необходимо возвести в наибольшую из тех степеней, с которыми он входит в данные числа.
- На последнем этапе производим умножение.
Пример: вычислим НОК чисел 252, 441 и 1080.
Разложим на множители:
\(252 = 2 \cdot 2 \cdot 3 \cdot 3 \cdot 7 = 2^2 \cdot 3^2 \cdot 7\)
\(441 = 3 \cdot 3 \cdot 7 \cdot 7 = 3^2 \cdot 7^2\)
\(1080 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3 \cdot 5 = 2^3 \cdot 3^3 \cdot 5\)
Среди множителей присутствуют числа 2, 3, 7, 5.
Выбираем для них самые высокие степени, которые есть в разложениях. Получается:
\(2^3, 3^3, 7^2\) \(\text {и } 5\)
Умножаем между собой:
\(2^3 \cdot 3^3 \cdot 7^2 \cdot 5\)\(= 52920\)
В результате получим, что НОК = 52920.
Вычисление НОК через НОД
Этот способ подходит, если нужно найти НОК двух чисел, для которых уже известен НОД. Для получения результата достаточно просто перемножить эти числа и разделить полученное произведение на НОД.
Пример: найти НОК чисел 36 и 48.
Сначала вычислим НОД этих чисел, например, через разложение на множители:
\(36 = 2^2 \cdot 3^2\)
\(48 = 2^4 \cdot 3\)
Перемножаем общие множители с минимальными степенями:
\(2^2 \cdot 3 = 12\)
\(\text{НОД} = 12\)
Теперь перемножим исходные числа:
\(36 \cdot 48 \)\(= 1728\)
Делим результат на НОД:
\(1728 \div 12 = 144\)
\(\text{НОК} = 144\)
Программы и онлайн-сервисы для расчета НОК и НОД
Рассчитать НОК и НОД можно при помощи специальных приложений и онлайн-сервисов. Их много, мы приведем несколько примеров.
Приложения для Android
Один из самых простых инструментов — Калькулятор НОД и НОК. С его помощью можно вычислять НОД и НОК для чисел количеством от двух до пяти.
В дополнение к основным функциям приложение может разложить числа на простые множители, сокращать дроби и приводить их к общему знаменателю.
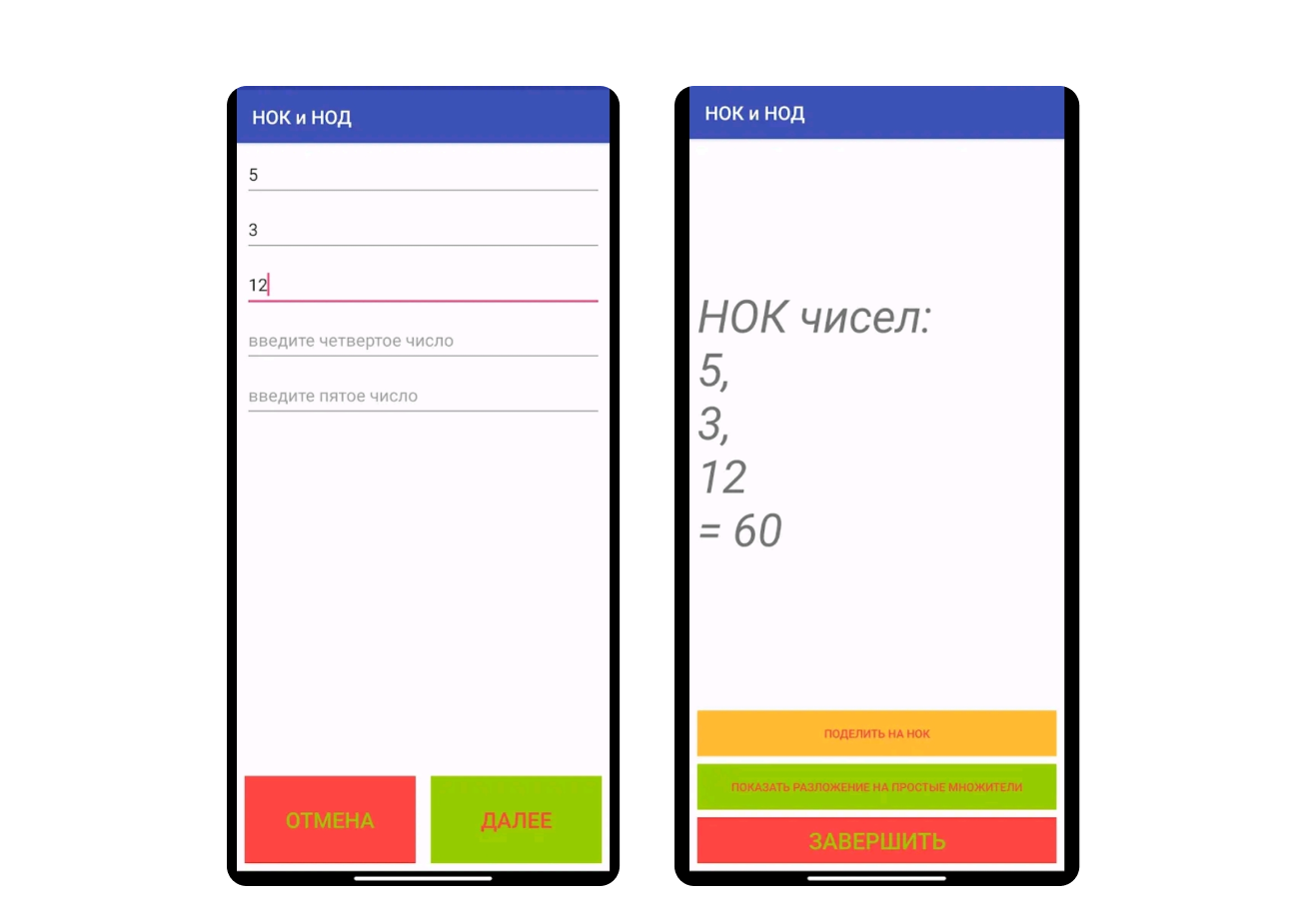
Результат вычисления НОК с помощью приложения
Приложения для iOS
В App Store доступно платное приложение для вычисления НОД и НОК от двух до четырех чисел. Сохраняет историю вычислений и может отправить результат по электронной почте.
Примеры вычислений НОК и НОД трех и четырех чисел, которые предоставил разработчик приложения
Программы Matlab и Scilab
В Matlab и Scilab встроен специальный язык программирования, с помощью которого можно производить разные расчеты. Команды на этом языке легко ввести в редактор и запустить на исполнение.
Например, чтобы вычислить НОК для двух чисел 45 и 36, в редакторе Matlab нужно ввести команду: g = lcm(45, 36)
Чтобы вычислить НОД для тех же чисел, следует ввести следующее: g = gcd(45, 36)
Результаты будут выведены в консоли.
Полезные материалы по использованию команд:
Онлайн-сервисы
Первый пример — калькулятор расчета НОК и НОД для двух чисел.
Второй пример — онлайн-калькулятор расчета НОД и НОК для двух и более чисел.
Оба онлайн-калькулятора выводят результаты в виде подробного решения, где расписан каждый шаг вычислений.
Решение задач с помощью НОД и НОК
Рассмотрим несколько математических задач, которые решаются с помощью НОД и НОК.
Задача 1:
Автомобиль проехал в первый день 560 километров, а во второй — 720 километрв. Скорость автомобиля во все дни была одинаковой и выражалась целым числом. Каждый день автомобиль был в пути целое число часов. Требуется найти максимально возможную скорость автомобиля, при которой он все еще будет проезжать указанные расстояния за целое число часов каждый день.
Решение: по условиям задачи нужно вычислить максимальную скорость автомобиля, поэтому делаем вывод, что нужно найти НОД чисел 560 и 720. Производим вычисление по любому алгоритму и узнаем, что НОД равен 80, а значит, скорость автомобиля равна 80 км/ч.
Задача 2:
На столе лежат журналы в количестве меньше 100 штук. Сколько всего на столе лежит журналов, если известно, что их можно связывать в отдельные пачки по 3, 4 и по 5 штук?
Решение: В этом случае надо найти НОК чисел 3, 4 и 5. Производим вычисление и узнаем, что он равен 60, а значит, на столе лежат 60 журналов.
Задача 3:
Сколько человек маршируют на площади, если они будут маршировать строем по 12 человек в шеренге и перестраиваться в колонну по 18 человек в шеренге?
Решение: Здесь снова требуется найти НОК. Ищем НОК чисел 12 и 18. Он равен 36, это значит, что на площади маршируют 36 человек.
Подведем итог
НОК — это наименьшее общее кратное двух и более чисел, а НОД — их наибольший общий делитель. Оба значения можно найти путем разложения чисел на множители, а еще вторым способом: для НОД — через алгоритм Евклида, для НОК — с помощью значения НОД двух чисел.
Помимо ручных расчетов, для поиска НОК и НОД можно использовать специальные сервисы: приложения, программы и онлайн-калькуляторы.
НОК и НОД используются в математике, теории чисел, компьютерных науках, инженерии и других технических и научных дисциплинах.
