Data Science — это во многом про математическую статистику. Без нее никуда, даже если вы хорошо программируете. Рассказываем про основные понятия статистики и о том, зачем они нужны.
Дата-сайентисты обрабатывают, анализируют данные, делают на основе информации выводы. Статистические показатели нужны как раз поэтому. С помощью статистики из данных извлекают полезные сведения.
Например, есть сырые данные о посещаемости сайта. Их много, поэтому специалист берет средние показатели и по ним видит основные характеристики выборки. А это уже ценные сведения, которые можно использовать для дальнейшего анализа.
Рассказываем, какие статистические методы и понятия нужно знать даже начинающему дата-сайентисту.
1. Мода, среднее, медиана и другие статистические показатели
Это базовые понятия, которые впервые можно услышать еще в школе. На уроках математики разбирают, что такое мода и медиана, но на самом деле показателей больше:
- мода — значение, которое встречается в выборке чаще всего;
- медиана — «серединное» значение. Если построить все данные в ряд по возрастанию, медианное значение окажется ровно посреди ряда: половина остальных значений меньше, половина больше. Медиана отличается от среднего тем, что не так чувствительна к аномально высоким или низким значениям;
- процентили, или перцентили — по смыслу похожи на медиану, но находятся не посередине. Например, 25 перцентиль означает, что 25% значений в выборке меньше него, а остальные больше;
- среднее — обычно имеется в виду среднее арифметическое, когда все значения складывают и делят на их количество. В отличие от медианы, не учитывает разброс;
- минимум и максимум — самое маленькое и самое большое значения;
- размах — разница между минимумом и максимумом;
- дисперсия — уровень разброса данных;
- смещение — нежелательные связи между данными.
Это не все. Понятий больше: отклонение, доверительные интервалы и многое другое.
2. Выборка и семплирование
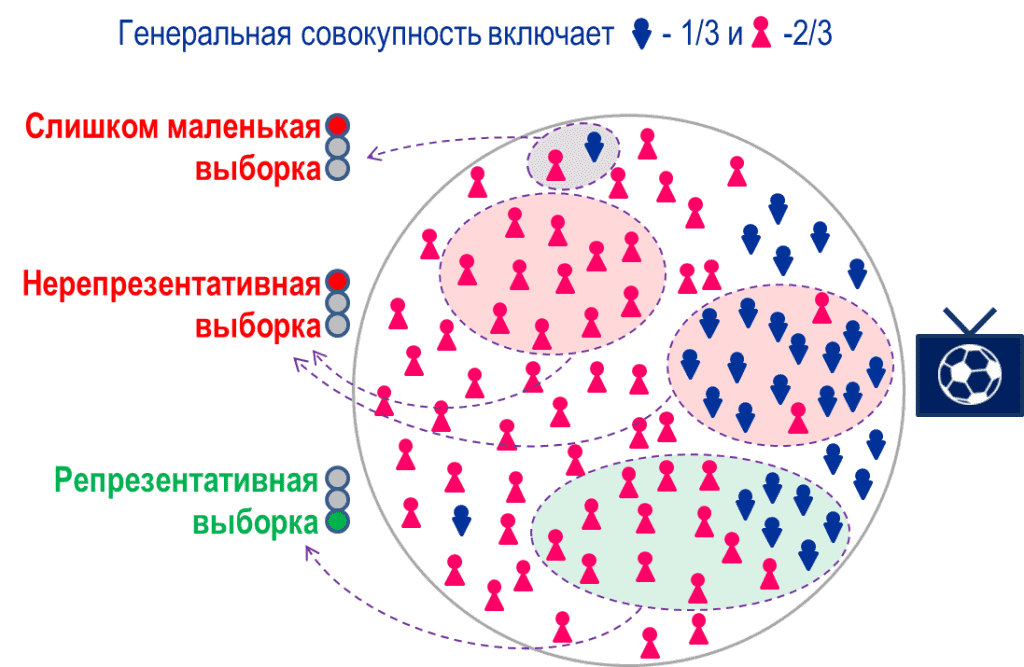
Собрать все доступные данные по вопросу часто невозможно. Нельзя опросить абсолютно всех пользователей интернета или посчитать все многоэтажки в мире. Поэтому берется выборка — определенный набор данных, который отражает реальную ситуацию.
Выборка должна быть репрезентативной. Это значит, что в ней нужно передать реальную картину происходящего — в статистике говорят «свойства генеральной совокупности».
Например, на сайте в равном количестве сидят мужчины и женщины, но 80% людей — пользователи до 30 лет. Если собирается выборка из пользователей, релевантной будет такая, где есть и мужчины, и женщины, причем в основном молодые. Пример упрощенный, но уже видно: если собрать выборку только из мужчин или только из людей за 30, она не покажет реальную ситуацию.
Репрезентативности помогает добиться семплирование. В упрощенном примере все более-менее понятно, но в реальности признаков больше. Часто генеральная совокупность огромна, поэтому нельзя сказать, например, сколько процентов домов в мире выше 10 этажей.
В таком случае специалисты используют семплирование, или семплинг — набор методов, которые помогают сделать выборку релевантной. Семплирование помогает составить правила для отбора данных в выборку. У него две главных цели:
- репрезентативность — выборка отражает реальную ситуацию;
- полнота — данных хватает для полноценного анализа.
В чистой математической статистике и в науке о данных определения семплирования немного различаются, равно как и его методы. Но общая цель одна — сделать хорошую выборку.
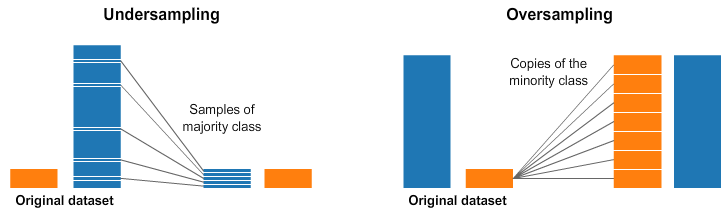
3. Овер- и андерсемплинг: когда размеры не совпадают
Два вида семплирования, которые стоит обсудить подробнее. Понятие используют в задачах классификации, когда нужно проанализировать данные и разделить на классы. Чаще всего этим занимаются специалисты по машинному обучению. Проблема начинается, когда аналитическая модель получает классы данных разного размера. Один класс больше (мажоритарный), другой меньше (миноритарный).
Например, два класса — пользователи моложе и старше 30 лет. В первом классе 2000 человек, в во втором всего 200. Разница в десять раз дает заметный перекос.
Если оставить все как есть, аналитическая модель может ошибиться. Например, в будущем начать относить все новые данные к мажоритарному классу. Поэтому классы балансируют: для этого как раз нужны оверсемплинг и андерсемплинг.
- Оверсемплинг — способ, когда данные в минориторном классе клонируют, чтобы их стало больше. Причем клонируют так, чтобы не нарушить изначальные соотношения значений и распределение.
- Андерсемплинг — способ, когда мажоритарный класс уменьшают. Проще всего убрать случайные значения, но чаще уменьшение опять же делается так, чтобы не нарушить соотношения.
При выборе метода нужно помнить о цене ошибки. Обычно она перекошена в сторону конкретного класса. Ошибочно причислить неплательщика к группе «можно дать кредит» более затратно для компании, чем причислить благополучного плательщика к группе «нельзя дать кредит». В таких случаях выбирают методы, которые фильтруют одну группу жестче, чем другую.
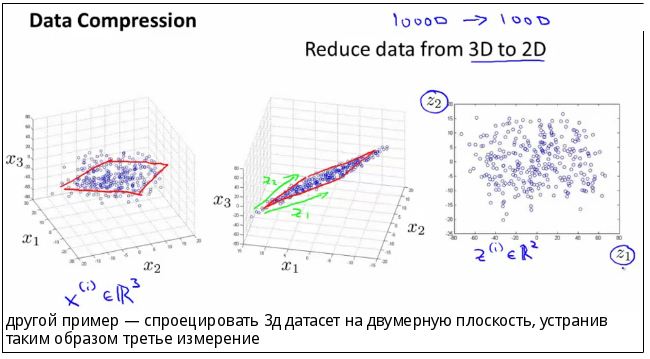
4. Уменьшение размерности
Даже грамотно отобранную выборку нужно «чистить» и уменьшать. Например, есть база пользователей — для каждого указаны пол, возраст, поведение, время захода на сайт, браузер, устройство и еще огромное количество показателей. Проанализировать их все слишком трудоемко и не всегда оправдано. В таких ситуациях требуется снижение размерности. Это уменьшение количества переменных, отбрасывание лишнего.
У снижения размерности есть два основных способа:
- отбор признаков — с помощью формул и векторных преобразований специалисты решают, какие признаки связаны с результатом или целевым показателем, а какие нет. Незначительные признаки отбрасывают;
- проекция признаков — показатели представляют на графике, а потом уменьшают размерность этого графика. Например, изначально он трехмерный — его делают двумерным. Некоторые точки трехмерного графика накладываются друг на друга и в двумерной версии выглядят как одна точка. Переменных становится меньше.
Внутри каждого способа есть разные стратегии, но основным считается так называемый метод главных компонент. Его используют чаще всего, причем для обоих способов.
5. Распределение вероятностей
Значения показателей в выборке могут быть более или менее вероятными. Для одних значений вероятность выше, для других ниже. То, как распределяются эти вероятности по разным значениям, и есть распределение. Так его описывает теория вероятностей и математическая статистика.
В науке о данных распределение можно считать не только для вероятности. Дата-сайентисты обобщают понятие как закон соответствия между одной и другой величиной. Классическое распределение вероятности — соответствие между значениями в выборке и вероятностью получить эти значения.
Равномерное распределение. Самый простой вариант — когда есть конкретные диапазоны значений со статичной вероятностью. График распределения состоит из прямых, горизонтальных и вертикальных линий. А если переменная категориальная, то есть может принимать несколько значений, ее изображают как несколько равномерных распределений.
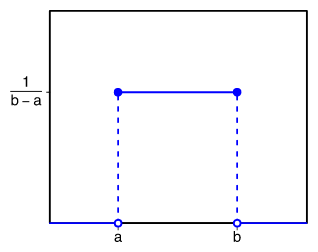
Нормальное распределение. Оно встречается чаще всего и в Data Science, и вообще в мире. Распределение на графике выглядит как холм, который называют колоколом Гаусса или гауссианой.
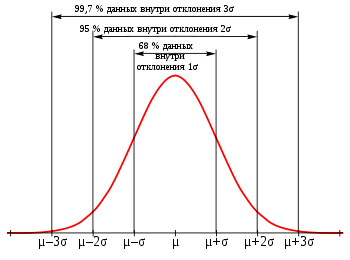
Колокол показывает: вероятность получить «среднее» значение больше всего. Чем больше отклонение от среднего, тем ниже вероятность. Для самых низких или высоких значений вероятность особенно низкая. Колокол может быть сдвинут влево или вправо относительно среднего — по медиане.
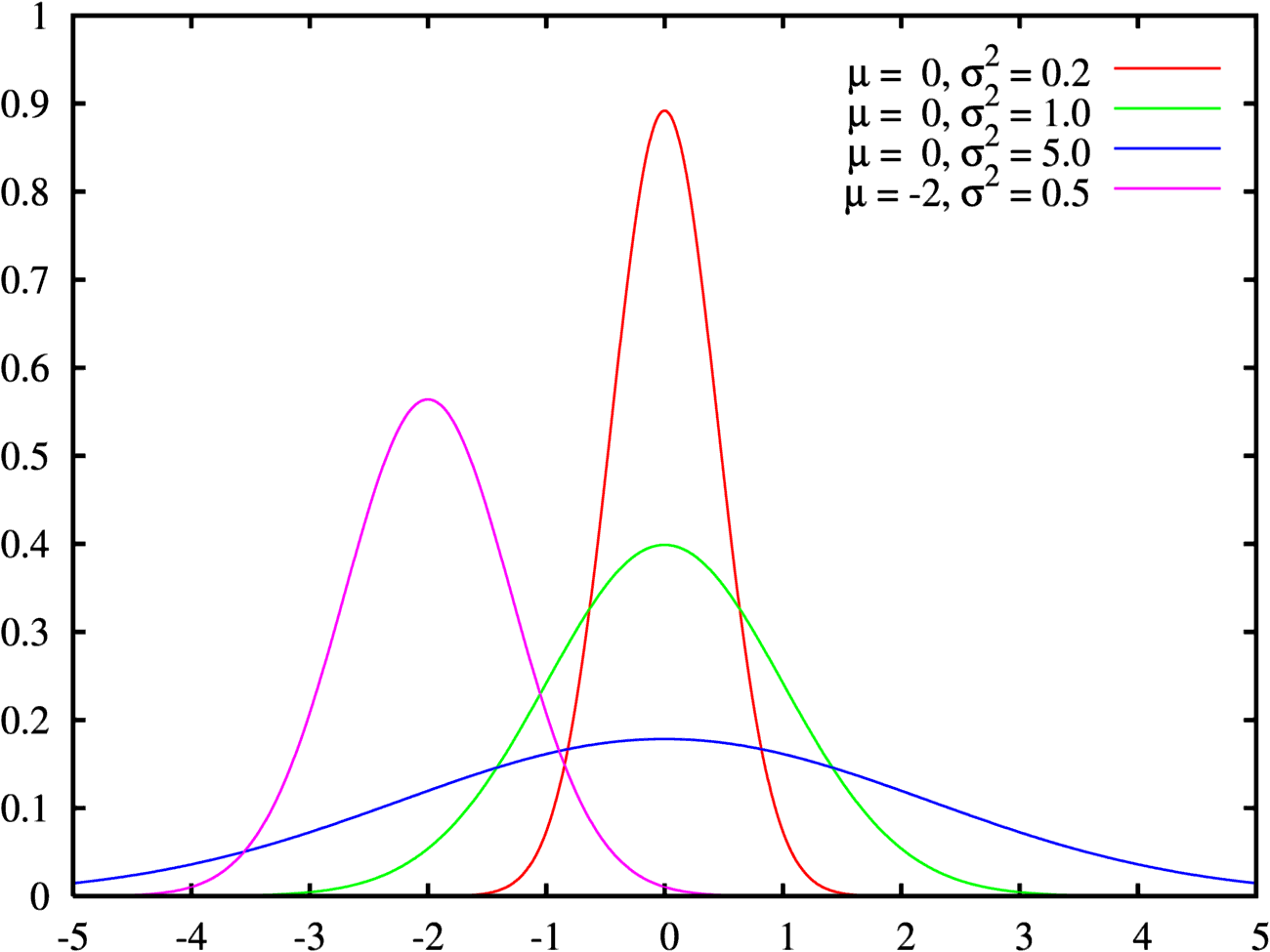
Считается, что нормально распределенными оказываются практически все величины, где результат зависит от огромного количества мелких факторов. Оно самое известное и часто встречающееся в природе, поэтому его и назвали нормальным.
Распределение Пуассона. В некоторых случаях очень похоже на нормальное. Распределение используют для анализа количества событий за определенный промежуток времени. События должны быть не связаны друг с другом. У распределения Пуассона есть дополнительный показатель интенсивности, который влияет на форму графика: чем выше, тем больше похоже на гауссиану.
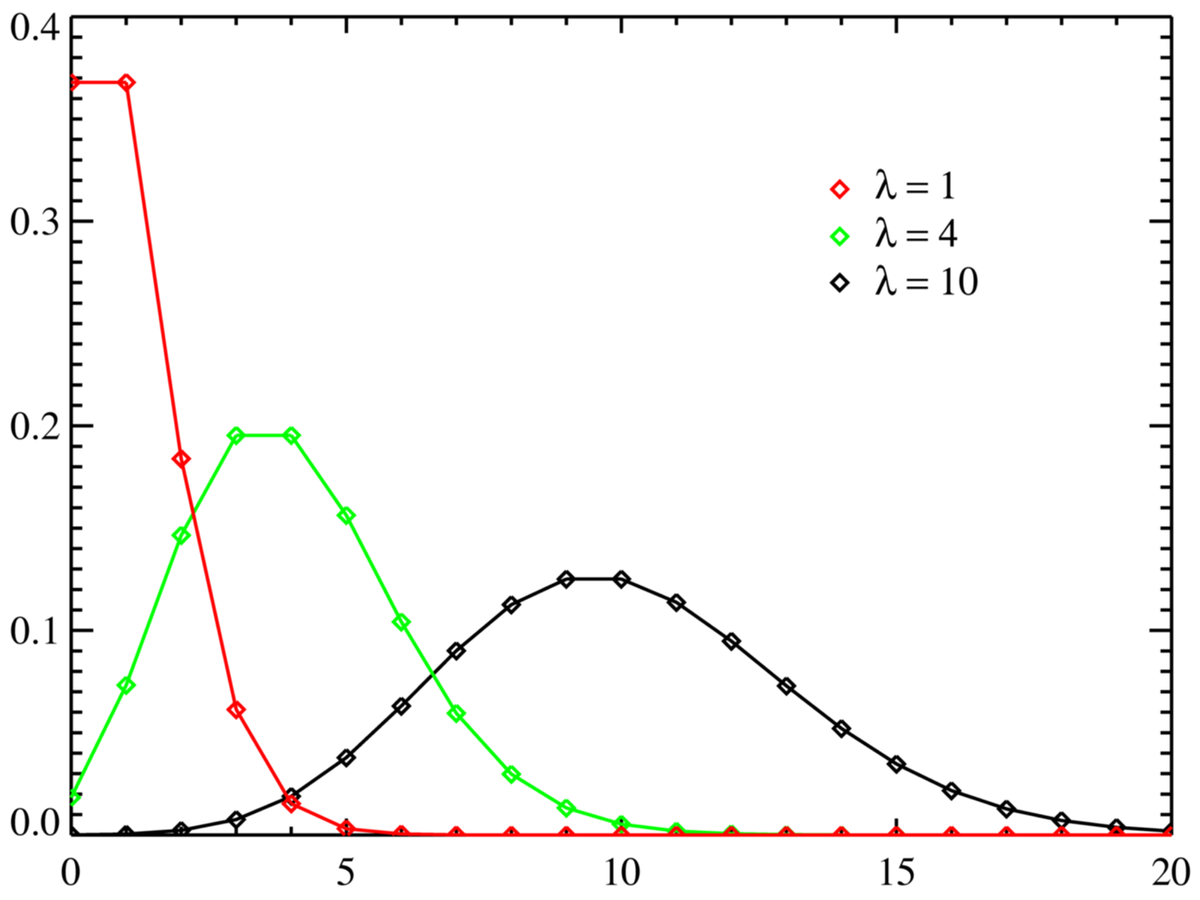
6. Смещение, дисперсия и связь между ними
Показатели влияют на огромное количество факторов: от формы графика распределения до точности результатов анализа.
Смещение. Это то, насколько данные и выводы из них «смещены» относительно реальной ситуации. Например, в выборку попали только блондины. Аналитическая модель увидела, что показатель встречается часто, и сочла его важным. В итоге по результатам аналитики оказалось, что в магазин заходят только светловолосые люди. Но это ведь не так!
Или знаменитая «ошибка выжившего»: есть много случаев, когда дельфины спасали людей, но те, кого они не спасли, уже не могут ничего рассказать. Поэтому складывается ложное ощущение, что дельфины спасают людей всегда, или смещение.
Обычно сильное смещение получается при неверно составленной выборке или при неправильной обработке данных. Например:
- систематическая ошибка отбора — когда в выборку попадают случаи только с одним результатом, а с другим не попадают. Кстати, именно так работает ошибка выжившего. Еще есть шуточный пример: «интернет-опрос показал, что 100% населения пользуется интернетом»;
- эффект низкой базы — когда в качестве стартового берется самое низкое значение, и относительно него любое увеличение показателя кажется огромным. Обратная ситуация называется эффектом высокой базы;
- ошибка меткого стрелка — в выборку попадают только похожие друг на друга значения, поэтому разброс оказывается меньше, чем нужно;
- уменьшение выборки или периода — из выборки намеренно или случайно убирают важную категорию результатов либо «обрезают» рассматриваемый период.
Смещение может возникать из-за намеренного манипулирования данными, а может быть результатом простой ошибки. Считается, что полностью избежать его почти невозможно.
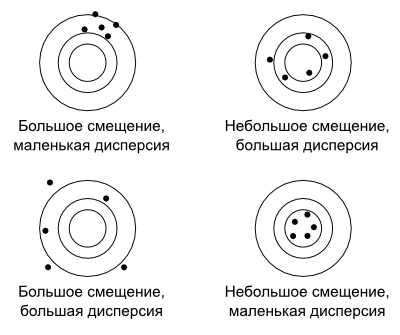
Дисперсия. Это уровень разброса значений относительно определенной точки. В качестве точки может выступать среднее, медиана, истинное или целевое значение — зависит от ситуации. Если все данные в выборке близки к этой точке — дисперсия низкая. Тогда говорят, что у данных высокая кучность. А если результаты «разбросаны» в большом диапазоне относительно точки, дисперсия высокая.
Показательный пример — мишень. Плохой стрелок стреляет с высокой дисперсией, а хороший стрелок бьет близко к центру мишени, и дисперсия получается низкая.
Дилемма смещения и дисперсии. Смещение и дисперсия обратно зависимы. Если мы корректируем выборку, чтобы уменьшить смещение, растет дисперсия. Если же стараемся уменьшить дисперсию, растет смещение.
Так происходит, потому что малый разброс дает более низкую объективность: повышается риск, что в выборку попадут только условные блондины. А если разброс высокий, попадут все, но зато такую выборку сложнее анализировать, и в результатах может получиться мешанина.
Поэтому одна из задач дата-сайентиста — найти компромисс, баланс между смещением и дисперсией, чтобы получить близкий к истине результат.
7. Корреляция (и ложная корреляция)
Корреляция — это явление, когда изменение одного показателя похоже на изменение другого показателя. Например, один растет, другой растет. Или один растет, другой падает — обратная корреляция.
- Линейная корреляция — один показатель меняется, другой меняется пропорционально первому.
- Нелинейная корреляция — показатели меняются непропорционально друг другу, а, например, экспоненциально. Такие корреляции отслеживают с помощью специальных методов анализа.
Важно. Корреляция — это не причинно-следственная связь. Иногда оба показателя просто зависят от третьих факторов. Или связаны еще сложнее. Или между ними вообще нет связи, а корреляция появилась из-за совпадения.
Если ошибочно принимать корреляцию за причинно-следственную связь, можно прийти к ложным выводам. Классическая ошибка: «Когда ввели ремни безопасности, больше людей оказалось в больницах». Это звучит как аргумент против ремней, но фактически корреляция означает, что люди стали чаще выживать в ДТП, а значит, попадать в больницы.
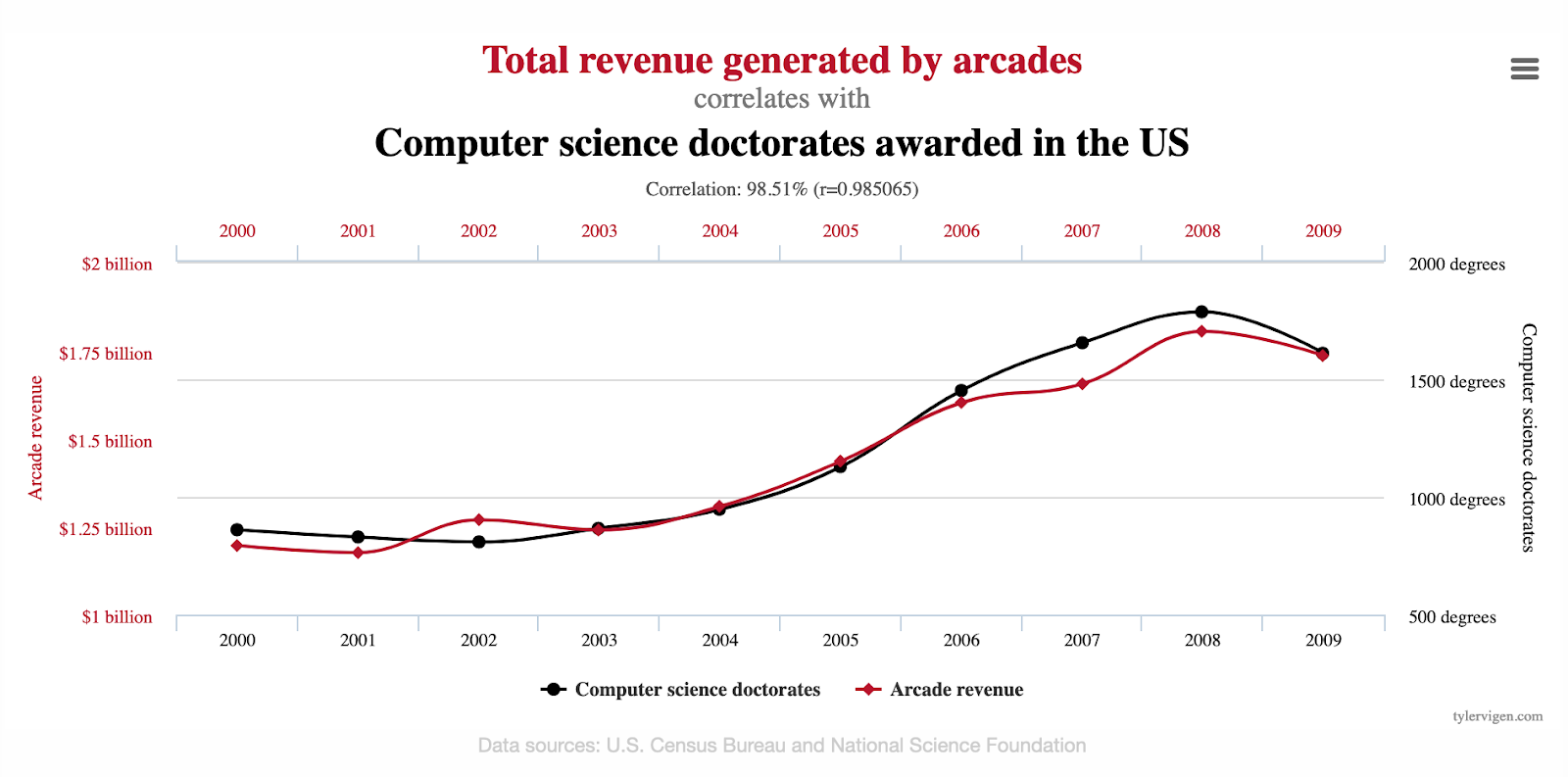
Ложные корреляции могут быть опасными, а могут быть забавными. Есть целый проект, который собирает абсурдные коррелирующие друг с другом факторы — между ними нет связи, но графики очень похожи.
8. Байесианская вероятность, чтобы менять ожидания
Теорема Байеса помогает подсчитать вероятность события с учетом каких-то гипотетических новых факторов. Классическая вероятность считается только с учетом так называемых априорных факторов: тех, что даны изначально. Если в процессе появится новое предположение или гипотеза, классическая вероятность это не учтет. А вот байесианская учтет.
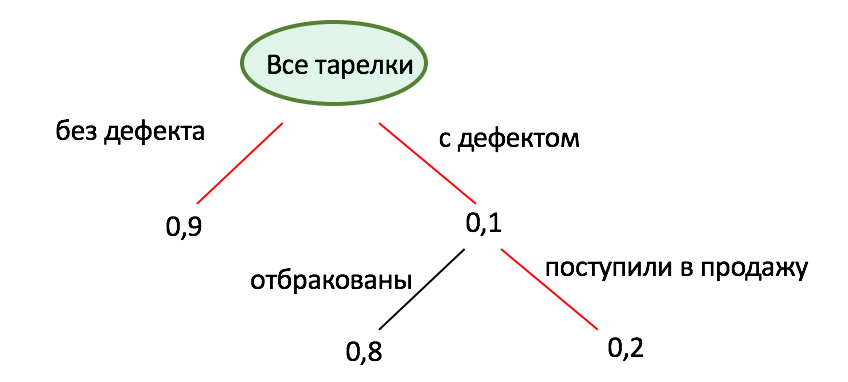
С теоремой связана так называемая формула полной вероятности. Чтобы ее посчитать, нужны обычная вероятность (так называемая частотная), а еще вероятность наступления какого-то нового фактора и вероятность получить какой-то другой результат, если этот новый фактор верен.