С помощью статьи доктора философии Оксфордского университета и автора книг о глубоком обучении Эндрю Траска показываем, как написать нейросеть на Python. Она умещается всего в девять строчек кода и выглядит вот так:
from numpy import exp, array, random, dot training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]]) training_set_outputs = array([[0, 1, 1, 0]]).T random.seed(1) synaptic_weights = 2 * random.random((3, 1)) — 1 for iteration in xrange(10000): output = 1 / (1 + exp(-(dot(training_set_inputs, synaptic_weights)))) synaptic_weights += dot(training_set_inputs.T, (training_set_outputs — output) * output * (1 — output)) print 1 / (1 + exp(-(dot(array([1, 0, 0]), synaptic_weights))))
Чуть ниже объясним как получается этот код и какой дополнительный код нужен к нему, чтобы нейросеть работала. Но сначала небольшое отступление о нейросетях и их устройстве.
Что такое нейросеть
Человеческий мозг состоит из ста миллиардов клеток, которые называются нейронами. Они соединены между собой синапсами. Если через синапсы к нейрону придет достаточное количество нервных импульсов, этот нейрон сработает и передаст нервный импульс дальше. Этот процесс лежит в основе нашего мышления.
Мы можем смоделировать это явление, создав нейронную сеть с помощью компьютера. Нам не нужно воссоздавать все сложные биологические процессы, которые происходят в человеческом мозге на молекулярном уровне, нам достаточно знать, что происходит на более высоких уровнях.
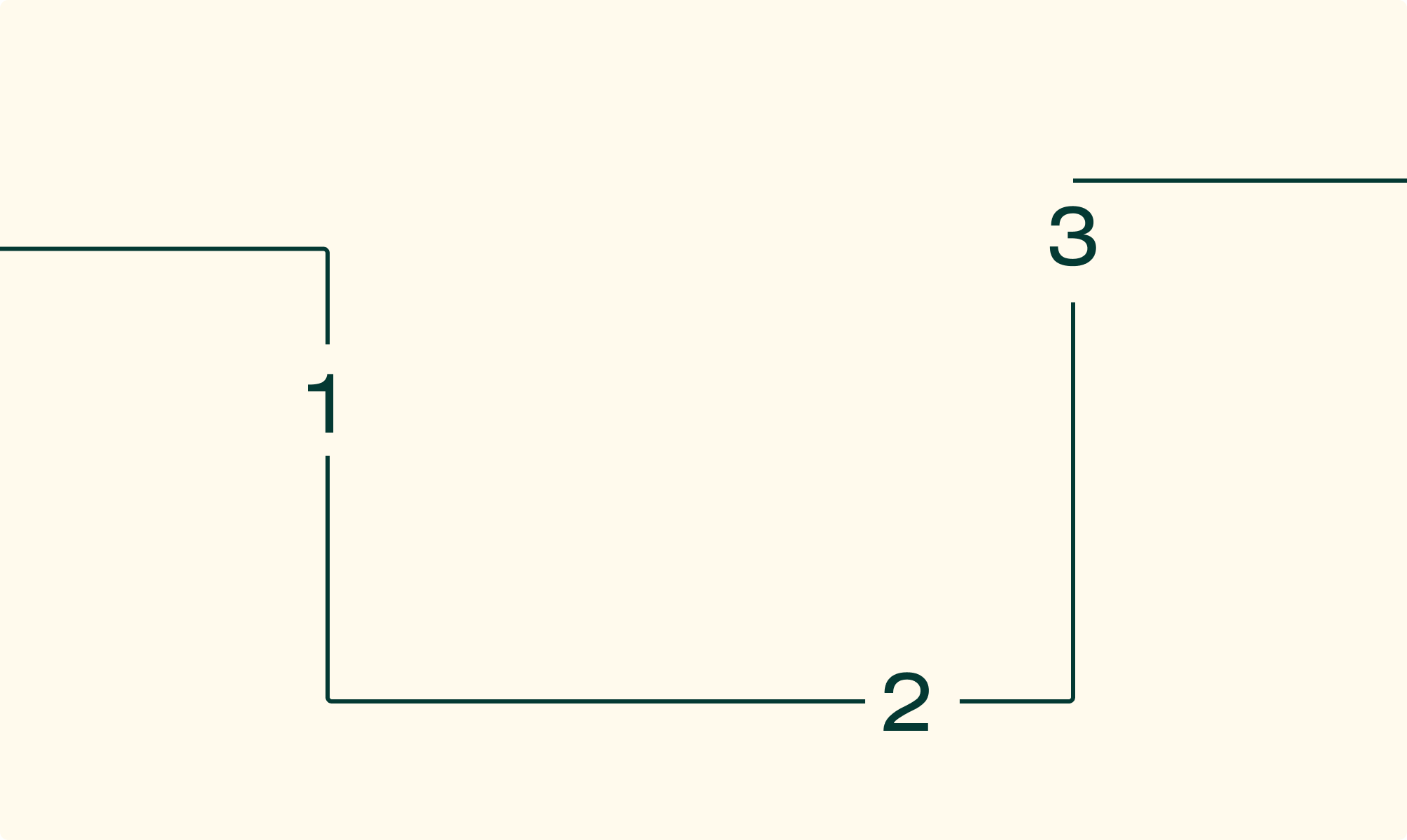
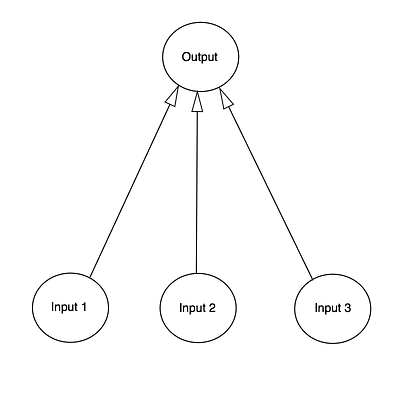
Для этого мы используем математический инструмент — матрицы, которые представляют собой таблицы чисел. Чтобы сделать все как можно проще, мы смоделируем только один нейрон, к которому поступает входная информация из трех источников и есть только один выход.
Наша задача — научить нейронную сеть решать задачу, которая изображена в ниже. Первые четыре примера будут нашим тренировочным набором. Получилось ли у вас увидеть закономерность? Что должно быть на месте вопросительного знака — 0 или 1?
| Входные данные | Вывод | ||
| 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | ? |
Вы могли заметить, что вывод всегда равен значению левого столбца. Так что ответом будет 1.
Пройдите наш тест и узнайте, какой контент подготовил искусственный интеллект, а какой — реальный человек. Ссылка в конце статьи.
Процесс тренировки
Но как научить наш нейрон правильно отвечать на заданный вопрос? Для этого мы зададим каждому входящему сигналу вес, который может быть положительным или отрицательным числом. Если на входе будет сигнал с большим положительным весом или отрицательным весом, то это сильно повлияет на решение нейрона, которое он подаст на выход. Прежде чем мы начнем обучение модели, зададим для каждого примера случайное число в качестве веса. После этого мы можем приняться за тренировочный процесс, который будет выглядеть следующим образом:
- В качестве входных данных мы возьмем примеры из тренировочного набора. Потом мы воспользуемся специальной формулой для расчета выхода нейрона, которая будет учитывать случайные веса, которые мы задали для каждого примера.
- Далее посчитаем размер ошибки, который вычисляется как разница между числом, которое нейрон подал на выход и желаемым числом из примера.
- В зависимости от того, в какую сторону нейрон ошибся, мы немного отрегулируем вес этого примера.
- Повторим этот процесс 10 000 раз.
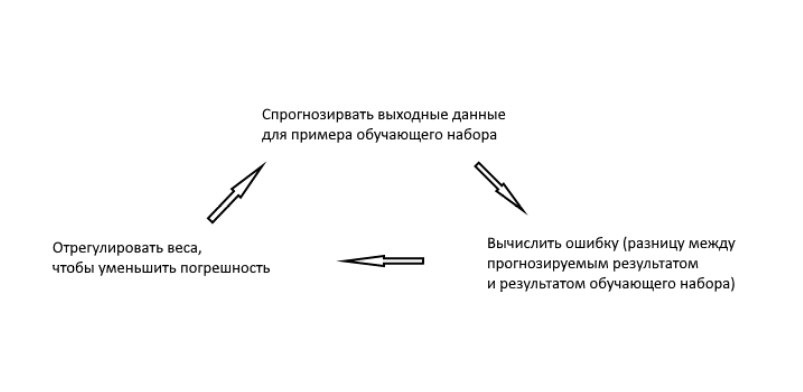
В какой-то момент веса достигнут оптимальных значений для тренировочного набора. Если после этого нейрону будет дана новая задача, которая следует такой же закономерности, он должен дать верный ответ.
Формула для расчета выхода нейрона
Разберем специальную формулу для расчета выхода нейрона. Сначала возьмем взвешенную сумму входов нейрона:
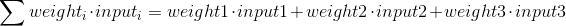
Затем мы нормализуем это, поэтому результат будет между 0 и 1. Для этого мы используем математически удобную функцию, называемую функцией Sigmoid:

На графике функция Sigmoid нарисует S-образную кривую.
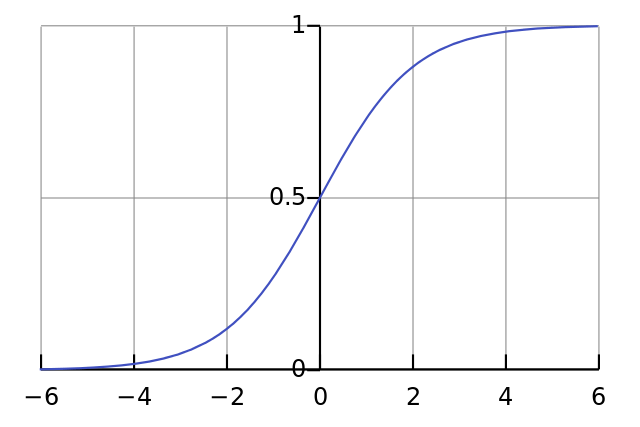
Путем замены первого уравнения во втором, получаем окончательное выражение для выхода нейрона.
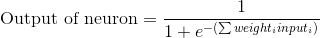
Формула корректировки весов
Во время тренировочного цикла (он изображен на рисунке 3) мы постоянно корректируем веса. Но на сколько? Для того, чтобы вычислить это, мы воспользуемся следующей формулой:
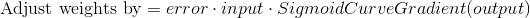
Давайте поймем почему формула имеет такой вид. Сначала нам нужно учесть то, что мы хотим скорректировать вес пропорционально размеру ошибки. Далее ошибка умножается на значение, поданное на вход нейрона, что, в нашем случае, 0 или 1. Если на вход был подан 0, то вес не корректируется. И в конце выражение умножается на градиент сигмоиды. Разберемся в последнем шаге по порядку:
- Мы использовали сигмоиду для того, чтобы посчитать выход нейрона.
- Если на выходе мы получаем большое положительное или отрицательное число, то это значит, что нейрон был весьма уверен в том или ином решении.
- На рисунке 4 мы можем увидеть, что при больших значениях переменной градиент принимает маленькие значения.
- Если нейрон уверен в том, что заданный вес верен, то мы не хотим сильно корректировать его. Умножение на градиент сигмоиды позволяет добиться такого эффекта.
Градиент сигмоиды может быть найден по следующей формуле:

Таким образом, подставляя второе уравнение в первое, конечная формула для корректировки весов будет выглядеть следующим образом:
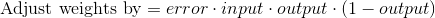
Существуют и другие формулы, которые позволяют нейрону обучаться быстрее, но преимущество этой формулы в том, что она достаточно проста для понимания.
Как написать это на Python
Хотя мы не будем использовать специальные библиотеки для нейронных сетей, мы импортируем следующие 4 метода из математической библиотеки numpy:
- exp — функция экспоненты
- array — метод создания матриц
- dot — метод перемножения матриц
- random — метод, подающий на выход случайное число
Теперь мы можем, например, представить наш тренировочный набор с использованием array():
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]]) training_set_outputs = array([[0, 1, 1, 0]]).T
Функция .T транспонирует матрицу из горизонтальной в вертикальную. В результате компьютер хранит эти числа таким образом:

Теперь мы готовы к более изящной версии кода. После нее добавим несколько финальных замечаний.
Обратите внимание, что на каждой итерации мы обрабатываем весь тренировочный набор одновременно. Таким образом наши переменные все являются матрицами.
Итак, вот полноценно работающий пример нейронной сети, написанный на Python:
from numpy import exp, array, random, dot class NeuralNetwork(): def __init__(self):
Задаем порождающий элемент для генератора случайных чисел, чтобы он генерировал одинаковые числа при каждом запуске программы:
random.seed(1)
Мы моделируем единственный нейрон с тремя входящими связями и одним выходом. Мы задаем случайные веса в матрице размера 3 x 1, где значения весов варьируются от -1 до 1, а среднее значение равно 0:
self.synaptic_weights = 2 * random.random((3, 1)) - 1
Функция сигмоиды, график которой имеет форму буквы S.
Мы используем эту функцию, чтобы нормализовать взвешенную сумму входных сигналов:
def __sigmoid(self, x): return 1 / (1 + exp(-x))
Производная от функции сигмоиды. Это градиент ее кривой. Его значение указывает насколько нейронная сеть уверена в правильности существующего веса:
def __sigmoid_derivative(self, x): return x * (1 - x)
Мы тренируем нейронную сеть методом проб и ошибок, каждый раз корректируя вес синапсов:
def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations): for iteration in xrange(number_of_training_iterations):
Тренировочный набор передается нейронной сети (одному нейрону в нашем случае):
output = self.think(training_set_inputs)
Вычисляем ошибку (разницу между желаемым выходом и выходом, предсказанным нейроном):
error = training_set_outputs - output
Умножаем ошибку на входной сигнал и на градиент сигмоиды. В результате этого, те веса, в которых нейрон не уверен, будут откорректированы сильнее. Входные сигналы, которые равны нулю, не приводят к изменению веса:
adjustment = dot(training_set_inputs.T, error * self.__sigmoid_derivative(output))
Корректируем веса:
self.synaptic_weights += adjustment
Заставляем наш нейрон подумать:
def think(self, inputs):
Пропускаем входящие данные через нейрон:
return self.__sigmoid(dot(inputs, self.synaptic_weights)) if __name__ == "__main__":
Инициализируем нейронную сеть, состоящую из одного нейрона:
neural_network = NeuralNetwork() print "Random starting synaptic weights:" print neural_network.synaptic_weights
Тренировочный набор для обучения. У нас это 4 примера, состоящих из 3 входящих значений и 1 выходящего значения:
training_set_inputs = array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])training_set_outputs = array([[0, 1, 1, 0]]).T
Обучаем нейронную сеть на тренировочном наборе, повторяя процесс 10000 раз, каждый раз корректируя веса:
neural_network.train(training_set_inputs, training_set_outputs, 10000) print "New synaptic weights after training:" print neural_network.synaptic_weights
Тестируем нейрон на новом примере:
print "Considering new situation [1, 0, 0] -> ?:" print neural_network.think(array([1, 0, 0]))
Этот код также можно найти на GitHub. Обратите внимание, что если вы используете Python 3, то вам будет нужно заменить команду “xrange” на “range”.
Несколько финальных замечаний
Попробуйте теперь запустить нейросеть на Python, используя в терминале эту команду:
python main.py
Результат должен быть таким:
Random starting synaptic weights:
[[-0.16595599]
[ 0.44064899]
[-0.99977125]]
New synaptic weights after training:
[[ 9.67299303]
[-0.2078435 ]
[-4.62963669]]
Considering new situation
[1, 0, 0] -> ?: [ 0.99993704]Ура, мы построили простую нейронную сеть с помощью Python!
Сначала нейронная сеть задала себе случайные веса, затем обучилась на тренировочном наборе. После этого она предсказала в качестве ответа 0.99993704 для нового примера [1, 0, 0]. Верный ответ был 1, так что это очень близко к правде!
Традиционные компьютерные программы обычно не способны обучаться. И это то, что делает нейронные сети таким поразительным инструментом: они способны учиться, адаптироваться и реагировать на новые обстоятельства. Точно так же, как и человеческий мозг.
Как можно улучшить нейронную сеть
Нейросеть, которую мы построили, решает очень простую задачу. Она обучилась на закономерности из таблицы и выдает правильный ответ. Но что, если усложнить задачу — например, цифр будет не две, а три, или результаты не будут иметь жесткой закономерности?
Так часто происходит в реальных задачах, например, при распознавании предметов. Не у всех из них есть жесткие критерии: скажем, гипертрофированного мультяшного персонажа мы по-прежнему различаем как человека, хотя у него совсем другие пропорции. Нейронную сеть сложно научить похожему — но современные системы могут справиться и с этим.
Конечно, для решения таких задач подобной нейросети не хватит. Понадобится больше нейронов, более сложные формулы и связи. Мы не будем сейчас делать сложную нейронную сеть: просто расскажем, за счет чего системы могут решать более трудные задачи.
Больше нейронов. В нашей тренировочной нейросети только один нейрон. Но если нейронов будет больше — каждый из них сможет по-своему реагировать на входные данные, соответственно, на следующие нейроны будут приходить данные с разных синапсов. Значит — больше вариативность, «подумать» и передать сигнал дальше может не один нейрон, а несколько. Можно менять и формулу передачи, и связи между нейронами — так получаются разные виды нейронных сетей.
Больше слоев. Наша нейронная сеть — однослойная. Но реальные нейросети, которые распознают картинки, решают математические задачи или рисуют, — все многослойные. Несколько слоев нужны для обработки данных.
Например, на вход поступает картинка. Чтобы нейросеть могла понять, что на ней изображено, она должна выделить разные элементы из картинки, распознать их и подумать, что означает сочетание этих элементов. Примерно так работает зрительная кора в головном мозге. Это несколько задач, их не смогут решить одинаковые нейроны. Поэтому нужно несколько слоев, где каждый делает что-то свое. Для распознавания часто используют так называемые сверточные нейросети. Они состоят из комбинации сверточных и субдискретизирующих слоев, каждый из которых решает свою задачу.
Лучше обучение. Искусственные нейронные сети обучаются примерно по тому же принципу, что живые существа. Когда человек часто повторяет одни и те же действия, он учится: ездить на велосипеде, рисовать или набирать текст. Это происходит, потому что веса между нейронами в мозгу меняются: нервные клетки наращивают новые связи, по-новому начинают воспринимать сигналы и правильнее их передают. Нейронная сеть тоже изменяет веса при обучении — чем оно объемнее, тем сильнее она «запомнит» какую-то закономерность.
Но нейронные сети — все же не человеческий мозг. Мозг сложнее, объемнее, в нем намного больше нейронов, чем в любой компьютерной нейросети. Поэтому чрезмерное обучение может сделать хуже. Например, переобученная нейросеть может начать распознавать предметы там, где их нет — так люди иногда видят лица в фарах машин и принимают пакеты за котов. А в случае с искусственной нейронной сетью такой эффект еще явнее и заметнее. Если же учить нейросеть на нескольких разнородных данных, скажем, сначала обучить считать числа, а потом — распознавать лица, она просто сломается и начнет работать непредсказуемо. Для таких задач нужны разные нейросети, разные структуры и связи.
Другие методы и формулы. Чтобы нейроны обучались, нужно задать формулу корректировки весов — мы говорили про это выше. Если нейронов много, то формулу нужно как-то распространить на все из них. Для этого используется метод градиентного спуска: рассчитывается градиент по весам, а потом от него делается шаг в меньшую сторону. Звучит сложно, но на самом деле для этого есть специальные формулы и функции.
Еще есть, например, метод обратного распространения ошибки — градиентный алгоритм для многослойных нейросетей. Сигналы ошибки, рассчитанные с помощью градиента, распространяются от выхода нейронной сети к входу, то есть идут не в прямом, а в обратном направлении.
На практике методов намного больше, они зависят от сложности и структуры нейросети, от функций ее активации и других параметров. Кстати, сигмоидальная функция — тоже не единственная: они разные, и каждая подходит для своих задач.
Больше мощностей. Нейронные сети работают с матрицами, так что если нейронов много, вычисления получаются очень ресурсоемкие. Известные нейросети вроде Midjourney или ChatGPT — это сложные и «тяжелые» системы, для их работы нужны сервера с мощным «железом». Так что написать собственный DALL-E на домашнем компьютере не получится. Но есть сервисы для аренды мощностей: ими как раз пользуются инженеры машинного обучения, чтобы создавать, обучать и тестировать модели.
Можно ли написать нейросеть еще короче
Да, можно, и даже более сложную. В этом примере мы использовали только одну математическую библиотеку и четыре метода из нее, чтобы показать расчеты нагляднее. Но есть множество специальных библиотек и фреймворков для создания именно нейросетей, например Tenzorflow или Pandas. Они ускоряют процесс. Например, можно создать слой из нескольких десятков, а то и сотен нейронов, в одну строчку. А еще парой строчек добавить новые слои и задать правила для обучения.
Конечно, мы создали модель всего лишь одного нейрона для решения очень простой задачи. Но что если мы соединим миллионы нейронов? Сможем ли мы таким образом однажды воссоздать реальное сознание?