Регрессия — это один из главных методов прогнозного моделирования и работы с data mining. Он позволяет установить связь между переменными, чтобы прогнозировать развитие какого-либо явления в будущем. Например, таким образом можно узнать, сколько товаров продаст магазин в ближайшие месяцы, как изменения цены повлияют на приток покупателей, какая доля сотрудников может уволиться из компании.
Про линейную и логистическую регрессию знают даже начинающие аналитики. Остальные функции этого класса реже оказываются на слуху, но настоящему профессионалу в области Data Science обязательно нужно знать, что они из себя представляют и для чего используются. Эти знания будут полезны и frontend-программистам, веб-разработчикам и всем, кто работает с данными в Python.
Сегодня мы устроим краткую экскурсию по разным видам регрессии, познакомимся с их возможностями и особенностями применения. Добавляйте эту статью в свою коллекцию шпаргалок и поехали. Инструменты для применения этих моделей в Python реализованы в библиотеках NumPy, scikit-learn, statsmodels.
Линейная регрессия
Начнем с самой простой модели, которая используется, если отношения между переменными линейны по своей природе. Например, линейная регрессия подскажет, сколько операторов колл-центра справятся с нагрузкой в горячий сезон или как пробег машины влияет на частоту ремонтов.
Если у вас одна независимая переменная (дескриптор), вы имеете дело с простой линейной регрессией. Если независимых переменных две и более, то это множественная линейная регрессия.
Главная особенность линейной регрессии в отсутствии выпадающих из общего тренда значений зависимой переменной и минимальном разбросе результатов. Кроме того, в этом случае между независимыми переменными нет взаимосвязи.
Логистическая регрессия
Вторая по популярности модель используется в тех случаях, когда зависимая переменная бинарна по своей природе, то есть попадает в одну из двух категорий. Например, вы хотите узнать, как те или иные факторы влияют на решение пользователя закрыть сайт или остаться на странице. Или вам нужно оценить шансы на успех у нескольких участников выборов (выиграет/не выиграет).
Логистическую регрессию можно также применять, если конечных вариантов больше двух. Скажем, вам нужно распределить учеников между гуманитарным, техническим и естественно-биологическим классами, используя результаты школьных экзаменов. В этом случае мы говорим о мультиномиальной, или множественной логистической регрессии.
Полиномиальная регрессия
Эта техника позволяет работать с нелинейными уравнениями, используя целые рациональные (полиномиальные) функции независимых переменных. Чтобы понять разницу между полиномиальной и линейной регрессией, взгляните на график ниже. Красная кривая гораздо лучше описывает поведение зависимой переменной, поскольку ее отношения с дескриптором нелинейны.
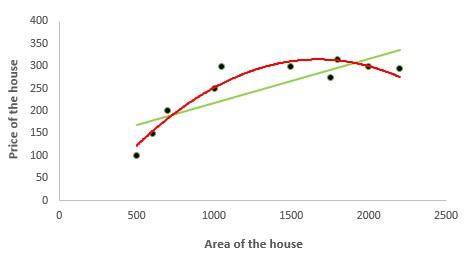
Полиномиальная регрессия помогает аналитикам и разработчикам решить проблему недообучения (underfitting), когда модель не охватывает значительную часть результатов. С другой стороны, нужно помнить, что неуместное применение этой техники или добавление ненужных, излишних характеристик создает риски переобучения (overfitting), из-за чего модель, которая показывает хорошие результаты на тренировочном сете окажется неприменима для работы с реальными данными.
Квантильная регрессия
Этот метод применяется, когда в данных присутствуют сильные искажения, часто встречаются выпадающие значения и случайные ошибки. Другими словами, если среднее значение, с которым работает линейная регрессия, неточно отражает взаимосвязь между переменными. В этих случаях квантильная регрессия позволяет ввести в расчеты целевую погрешность, или задать квантили — значения, которое результирующие переменные не будут превышать.
Для применения квантильной регрессии в Python вам понадобится пакет statsmodels. С его помощью вы сможете анализировать информацию с помощью настраиваемых квантилей, получая возможность смотреть на данные под разными углами.
Лассо-регрессия / Ридж-регрессия
Эти две техники применяются, если вам нужно уменьшить размерность данных и устранить проблему переобучения. Для этого применяются два способа:
- L1-регуляризация — добавляет штраф к сумме абсолютных значений коэффициентов. Этот метод используется в лассо-регрессии.
- L2-регуляризация — добавляет штраф к сумме квадратов коэффициентов. Этот метод используется в ридж-регрессии.
В большинстве случаев исследователи и разработчики предпочитают L2-функцию — она эффективнее с точки зрения вычислительных функций. С другой стороны, лассо-регрессия позволяет уменьшить значения некоторых коэффициентов до 0, то есть вывести из поля исследования лишние переменные. Это полезно, если на какое-либо явление влияют тысячи факторов и рассматривать все их оказывается бессмысленно.
Оба метода регуляризации объединены в технике эластичной сети. Она оптимально подходит, когда независимые переменные сильно коррелированы между собой. В этих случаях модель сможет попеременно применять L1- и L2-функции, в зависимости от того, какая лучше подходит с учетом входных данных.
Метод главных компонент
Анализ главных компонент (Principal Components Analysis) — это еще один способ уменьшить размерность данных. Он построен на создании ключевых независимых переменных, которые оказывают наибольшее влияние на функцию. Таким образом можно построить регрессионную модель на основе сильно зашумленных данных. На первом этапе аналитик определяет среди них главные компоненты, далее применяет к ним необходимую функцию.
Важно понимать, что основные компоненты, с которыми аналитик работает в этом случае, фактически представляют собой функцию остальных характеристик. Именно поэтому мы говорим о создании ключевых переменных, а не вычленении их из общего числа. По этой причине применение PCA не подходит для объяснения фактических связей между переменными — это скорее создание имитационной модели на основе известных данных о том или ином явлении.
Регрессия наименьших частичных квадратов
В отличие от предыдущей техники, метод наименьших частичных квадратов (Partial Least Squares, PLS) принимает во внимание зависимую переменную. Это позволяет строить модели с меньшим количеством компонентов, что очень удобно в тех случаях, если количество предикторов сильно превышает количество зависимых переменных или если первые оказываются сильно коррелированы.
Технически PLS сильно напоминает PCR — сначала определяются скрытые факторы, которые объясняют взаимосвязь переменных, затем по этим данным выстраивается прогноз.
Порядковая регрессия
Этот метод позволяет изучать явления в привязке к значениям каких-либо шкал. Например, когда речь идет об отношениях пользователей к дизайну сайта — от “совсем не нравится” до “очень нравится”. Или в медицинских исследованиях таким образом можно понять, как меняются ощущения пациентов (от “очень сильной боли” до “совсем нет боли”).
Почему для этого нельзя применять линейную регрессию? Потому что она не учитывает смысловую разницу между разными разрядами шкалы. Возьмем для примера трех людей ростом в 175 см и весом в 55, 70 и 85 кг. 15 килограммов, на которые самый худой и самый тучный человек отстоят от участника со средним показателем, для линейной функции имеют одинаковое значение. А с точки зрения социологии и медицины это разница между ожирением, дистрофичностью и нормальным весом.
Регрессия Пуассона / Отрицательная биноминальная регрессия
Еще две техники, которые используются для особых ситуаций, в данном случае — когда вам нужно пересчитать некие события, которые произойдут независимо друг от друга на протяжении заданного промежутка времени. Например, спрогнозировать количество походов покупателей в магазин за каким-то конкретным продуктом. Или количество критических ошибок на корпоративных компьютерах. Такие явления происходят в соответствии с распределением Пуассона, откуда техника и получила свое название.
Недостатком этого метода является то, что при его использовании распределение зависимых переменных оказывается равным их средним значениям. В реальности аналитики нередко сталкиваются с высокой дисперсией наблюдаемых явлений, которая значительно отличается средних показателей. Для таких моделей используется отрицательная биноминальная регрессия.
Специфика этих регрессий обуславливает определенные требования к зависимым переменным: они должны выражаться целыми, положительными числами.
Регрессия Кокса
Последняя в нашей подборке модель используется для оценки времени до определенного события. Какова вероятность, что сотрудник проработает в компании 10 лет? Сколько гудков готов ждать клиент, прежде чем положит трубку? Когда у пациента наступит следующий кризис?
Модель работает на основе двух параметров: один отражает течение времени, второй, бинарный показатель определяет, случилось событие или нет. Это напоминает механику логистической регрессии, однако та техника не использует время. Основополагающие предположения для регрессии Кокса состоят в том, что между независимыми переменными нет корреляции и все они линейно влияют на ожидаемое событие. Кроме того, в любой отрезок времени вероятность наступления события для любых двух объектов должна быть пропорциональна.
Это не полный список регрессий, которые доступны разработчикам и аналитикам в Python. Однако даже этот перечень дает представление о том, какие возможности для изучения самых разных данных открывает этот язык.







