Рекурсия в Python: что это такое и где может пригодиться

Наверняка все в детстве создавали бесконечный коридор, ставя друг напротив друга два зеркала. Этот коридор — наглядный пример рекурсии. В этой статье мы расскажем, что такое рекурсия, как она работает и разберем несколько интересных функций, в которых используется этот принцип.

9 месяцев

Python-разработчик

Изучайте Python эффективно — с программой, практикой и наставником

4 030 ₽/мес

6 717 ₽/мес

Подробнее

Python-разработчик

Что такое рекурсия

Рекурсия — это случай, когда функция вызывает саму себя. 

Рассмотрим простой пример. Предположим, что нам нужно написать функцию, которая выводит последовательность натуральных чисел от 1 до 10. Для решения этой задачи мы можем использовать цикл for:

def countup(n):
    for i in range(1, n+1):
        print(i)

И потом вызвать эту функцию таким образом:

countup(10)

В консоли получим такой вывод:

1
2
3
4
5
6
7
8
9
10

Используя цикл, мы применили к решению поставленной задачи так называемый итеративный подход. С помощью рекурсии код функции будет выглядеть так:

def countup(n):
    if n >= 1:
        countup(n - 1)
        print(n)

Как видно, функция вызывает саму себя только при выполнении определенного условия. В нашем случае аргумент n должен быть больше или равен единице. Без этого условия при запуске функции мы получим следующую ошибку:

[Previous line repeated 996 more times]
RecursionError: maximum recursion depth exceeded

Это означает, что стек переполнен. Стек — это структура данных, работающая по принципу LIFO (last in, first out), что в переводе означает «последним пришел — первым ушел». Стек можно представить в виде стопки бумаг: каждый новый лист кладется сверху, а извлекать их нужно начиная с верхнего.

Переполнение стека следует избегать. Если при выполнении функции есть высокая вероятность столкнуться с этим, лучше выбрать итеративный подход.

Обычно в Python глубина стека ограничена примерно 1000 вызовами, но это значение можно увеличить. Для этого в начале программы добавьте следующий код:

import sys

sys.setrecursionlimit(2000)

В данном случае этот код устанавливает лимит в 2000 вызовов.

Как работает рекурсия в Python

Рассмотрим функцию countup более подробно. Допустим, аргумент n равен 10. Так как 10 больше единицы, происходит рекурсивный вызов функции countup, но уже с аргументом, уменьшенным на единицу — то есть с 9. Следом в коде стоит команда вывода числа 10, но сразу в консоль ничего не выводится — эта команда сохраняется в стеке.

Внутри вызванной функции снова происходит проверка условия и вызов countup с аргументом 8. Команда вывода числа 9 также отправляется в стек.

Так продолжается до тех пор, пока выполняется условие. Как только условие перестанет выполняться, начнется развертывание стека. Все отложенные команды начнут выполняться в обратном порядке. Так как стек работает по принципу LIFO, в результате мы увидим последовательность чисел от 1 до 10.

Теперь рассмотрим функцию, которая демонстрирует два основных элемента рекурсии: базовый случай и рекурсивный случай. Эта функция вычисляет факториал числа:

def factorial(n):
    if n == 1:  # Базовый случай
        return n
    else: # Рекурсивный случай
        return n * factorial(n - 1)

Факториал числа — это произведение всех натуральных чисел от единицы до самого этого числа включительно. Например:

6! = 1 * 2 * 3 * 4 * 5 * 6 = 720

В этой функции возврат значения n, когда оно равно 1, называется базовым случаем. Возврат результата с рекурсивным вызовом функции — это рекурсивный случай.

Теперь рассмотрим функцию посложнее, в которой уже два базовых случая. Она предназначена для вычисления чисел из последовательности Фибоначчи:

def fibonacci(n):
    if n == 0:  # Базовый случай
        return 0
    elif n == 1 or n == 2:  # Базовый случай
        return 1
    else:  # Рекурсивный случай
        return fibonacci(n - 1) + fibonacci(n - 2)

На вход функции подается порядковый номер числа в последовательности. Последовательность Фибоначчи — это такая числовая последовательность, в которой первые два числа — 0 и 1, а каждое следующее равно сумме двух предыдущих. Пример:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …

Ниже приводится функция, способная возводить числа в степень с помощью рекурсии:

def power(a, n):
    if n == 0:   # Базовый случай
        return 1
    elif n % 2 == 1:  # Рекурсивный случай
        return power(a, n - 1) * a
    else:  # Рекурсивный случай
        return power(a, n // 2) ** 2

Как видно, эта функция содержит один базовый и два рекурсивных случая. Если с вычислением факториала и чисел Фибоначчи все довольно просто, то здесь стоит пояснить, откуда берутся именно такие формулы в рекурсивных вызовах функции.

Дело в том, что в данном случае используется алгоритм быстрого возведения в степень. Суть этого алгоритма в том, что при нечетном показателе степени применяется следующая формула:

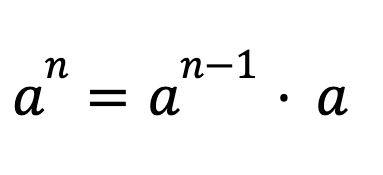
Это как раз первый рекурсивный случай, в котором проверяется, равен ли остаток от деления показателя степени на 2 единице. Как известно, если при делении на два в остатке получается единица, то число нечетное. В противном случае применяется следующая формула:

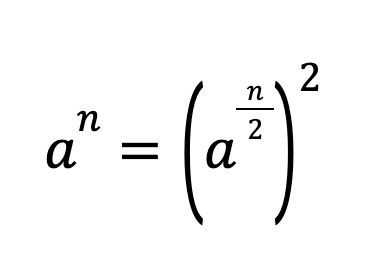
Такой подход позволяет сократить количество операций умножения при возведении в степень.

Базовый случай обычно содержит самое простое решение задачи, которое не требует дальнейших рекурсивных вызовов. Другими словами, базовый случай — это условие, при котором функция прекращает вызывать саму себя.

Если базового случая нет, рекурсия может стать бесконечной, что приведет к переполнению стека.

Станьте разработчиком на Python и решайте самые разные задачи: от написания кода до автоматизации процессов

Подробнее

Еще примеры рекурсий

Рассмотрим еще три примера применения рекурсии.

Удаление файлов

Следующий пример позволяет удалять файлы при помощи рекурсии:

ИСПОЛЬЗУЙТЕ ЭТОТ КОД С ОСТОРОЖНОСТЬЮ! МОЖНО СЛУЧАЙНО УДАЛИТЬ ВАЖНЫЕ ФАЙЛЫ.

def delete_files(path, file_name):
    files = os.listdir(path)
    for f in files:
        p = os.path.join(path, f)
        if os.path.isdir(p):
            print(p)
            if f == file_name:
                shutil.rmtree(p, True)
            else:
                delete_files(p, file_name)
        else:
            if f == file_name:
                os.remove(p)

Перед использованием данной функции необходимо сделать соответствующие импорты. В самом начале исходника пишем:

import os
import shutil

Как это все работает? Функция принимает на вход путь к папке path и имя файла file_name. Сначала с помощью метода listdir формируется список файлов и папок, который сохраняется в переменную files.

Затем запускается цикл for, в котором перебираются все элементы списка. Для каждого элемента проверяется, является ли он директорией.

• Если это папка, ее удаление выполняется с помощью метода rmtree из модуля shutil.
• Если это обычный файл, он удаляется с помощью метода remove из модуля os.

Рекурсивный вызов функции происходит только в том случае, если папка с указанным именем не найдена и требуется продолжить поиск в подкаталогах.

Ханойская башня

Далее рассмотрим решение головоломки под названием «Ханойская башня»:

def hanoi_tower(a, b, c, n):
    if n == 1:
        print(a, '->', c)
    else:
        hanoi_tower(a, c, b, n - 1)
        print(a, '->', c)
        hanoi_tower(b, a, c, n - 1)

Сама головоломка представляет собой три штыря (иногда их бывает больше), на один из которых надето несколько колец разного размера. Задача — переместить все кольца с одного штыря на другой, следуя двум правилам:

1. За один ход можно переложить только одно кольцо.
   
2. Нельзя класть большее кольцо на меньшее.

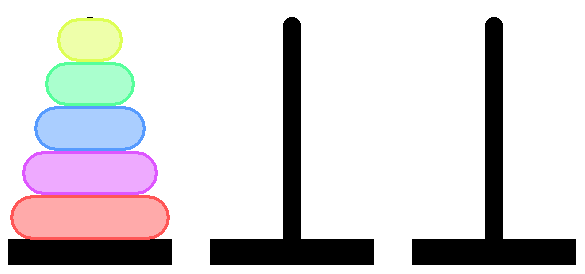
В приведенной функции аргументы a, b и c обозначают три башни (штыря), а n — количество колец.

Если n равно 1, задача решается одним действием: переносим кольцо со штыря A на штырь C. Если n больше 1, подключаются рекурсивные вызовы, каждый раз с уменьшенным значением n, поскольку одно перемещение уже произошло на предыдущем шаге.

Функцию можно вызвать, например, так:

hanoi_tower("A", "B", "C", 5)

В этом примере используется 5 колец — это довольно популярный вариант задачи. При запуске функции с таким параметром мы получим следующий порядок действий:

A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
A -> B
C -> B
C -> A
B -> A
C -> B
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C
B -> A
C -> B
C -> A
B -> A
B -> C
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C

Что-то многовато ходов. Для наглядности уменьшим количество колец до двух:

hanoi_tower("A", "B", "C", 2)

Результат:

A -> B
A -> C
B -> C

Теперь все выглядит гораздо проще. С первого штыря перемещаем кольцо на второй штырь. Потом с первого штыря переносим оставшееся кольцо на третий штырь и последним ходом укладываем на него кольцо со второго штыря.

Проверка на палиндром

Теперь рассмотрим функцию, которая производит проверку строки на палиндром:

def is_palindrome(s):
    if len(s) < 1:
        return True
    else:
        if s[0] == s[-1]:
            return is_palindrome(s[1:-1])
        else:
            return False

Палиндром — это строка, которая одинаково читается как слева направо, так и справа налево.

Приведенная выше функция обрезает строку с концов и проверяет, совпадают ли первый и последний символы. Если символы равны, выполняется рекурсивный вызов, и процесс обрезки и проверки повторяется. Если символы не совпадают, функция возвращает False.

В качестве базового случая используется условие, при котором длина строки меньше единицы. В этом случае функция возвращает True, так как пустая строка или одиночный символ считаются палиндромами.

Вызвать функцию можно, например, так:

s = str(input("Введите строку: "))
if (is_palindrome(s) == True):
    print("Это палиндром!")
else:
    print("Это не палиндром!")

Пример работы программы:

Введите строку: шалаш
Это палиндром!

Далее предлагаем выполнить три несложных задания.

Задания для самостоятельного выполнения

Напишите три функции с рекурсией:

1. Функцию, которая выводит в консоль натуральные числа от n до 1.
2. Функцию, которая вычисляет сумму целых чисел от 1 до n.
3. Функцию, которая определяет длину строки.

 def countdown(n):
  if n == 1:
     print("1")
  else:
     print(n)
     countdown(n - 1)

countdown(10)

10
9
8
7
6
5
4
3
2
1

def sum_numbers(n):
    if n == 1:
        return 1
    else:
        return n + sum_numbers(n - 1)

print(sum_numbers(6))

21

def string_length(s):
    if s == '':
        return 0
    else:
        return 1 + string_length(s[1:])

print(string_length("Рекурсия"))

8

Python-разработчик

Освойте Python с нуля. Подготовим к трудоустройству: дадим много практики, реальные проекты для портфолио, поможем с резюме. Лучшие студенты пройдут стажировки в проектах компаний-партнеров.

Подробнее

Python-разработчик