Многие начинающие ML-инженеры и аналитики с головой уходят в нейросети, градиентные бустинги и красивые дашборды, пропуская основы статистики. А зря! Ведь именно статистика помогает нам не обманывать самих себя и принимать решения, основанные на данных, а не на интуиции или случайности.
Поговорим на тему, которая на первый взгляд кажется скучной и академической, но на деле является одним из самых мощных инструментов в арсенале любого специалиста по данным — речь пойдет о статистической значимости.
Зачем специалисту по машинному обучению понимать в статистике?
Представьте, вы неделями работали над новой версией модели, которая предсказывает отток клиентов. Вы добавили новые признаки, подобрали гиперпараметры и, наконец, запустили тест. Результат: точность на тестовой выборке выросла с 85% до 85.5%. Победа? Стоит ли срочно выкатывать новую модель в продакшн, переписывать код и радоваться успеху?
А что, если эти 0.5% — просто статистический шум? Может, вам просто повезло с тестовой выборкой, и на реальных данных новая модель окажется даже хуже старой?
В машинном обучении мы постоянно что-то сравниваем:
- Стала ли модель лучше после изменений?
- Влияет ли новый признак на точность предсказаний?
- Действительно ли версия сайта А приносит больше конверсий, чем версия Б?
Статистическая значимость — это наш надежный способ понять, являются ли наблюдаемые нами изменения реальным эффектом или просто случайностью. Это как фильтр, который отделяет настоящий сигнал от фонового шума. Без этого фильтра мы рискуем тратить время и деньги на внедрение бесполезных улучшений или, что еще хуже, ломать то, что и так хорошо работало.
Основа основ: что такое гипотезы?
В основе любого статистического теста лежат две конкурирующие идеи — две гипотезы. Это похоже на судебный процесс: есть «презумпция невиновности» и есть обвинение, которое пытается ее опровергнуть.
Нулевая гипотеза (H0): Предположение об отсутствии эффекта.
Простыми словами: Это базовое, «скептическое» предположение, что ничего не изменилось. Это статус-кво. Мы как бы говорим: «Мои нововведения — пустышка, и любой результат, который я вижу, — это просто случайность». Нулевая гипотеза — это то, что мы пытаемся опровергнуть.
Аналогия:
В медицине H0: «Новое лекарство работает не лучше, чем таблетка с сахаром (плацебо)».
В нашем мире ML: «Новый признак, который я добавил в модель, никак не влияет на ее точность».
В A/B тесте: «Новый дизайн кнопки не изменил количество кликов».
Альтернативная гипотеза (H1 или HA): То, что мы хотим доказать.
Простыми словами: Это наше утверждение, противоположное нулевой гипотезе. Оно гласит, что эффект, который мы наблюдаем, — реален и не случаен. Это то, на что мы надеемся.
Аналогия:
В медицине H1: «Новое лекарство действительно лечит лучше, чем плацебо».
В ML: «Новый признак значительно улучшает точность модели».
В A/B тесте: «Новый дизайн кнопки действительно влияет на количество кликов».
Весь процесс статистической проверки — это попытка собрать достаточно доказательств, чтобы с уверенностью отвергнуть нулевую гипотезу в пользу альтернативной.
Волшебное P-value: что это такое простыми словами?
Итак, у нас есть две гипотезы. Как выбрать между ними? Здесь на сцену выходит наш главный герой — p-value (или p-значение).
P-value — это вероятность получить наблюдаемые (или даже более экстремальные) результаты при условии, что нулевая гипотеза верна.
Звучит сложно? Давайте переведем.
Супер-простое объяснение: P-value отвечает на один-единственный вопрос: «Если на самом деле никаких изменений нет (H0 верна), то каков шанс увидеть такой результат, как у меня, или даже круче, чисто случайно?»
Низкое p-value (обычно < 0.05): «Ух ты! Шанс получить такой результат случайно — исчезающе мал». Это означает, что наши данные очень сильно противоречат нулевой гипотезе. Мы получаем весомый аргумент, чтобы ее отвергнуть и принять альтернативную. Результат статистически значим.
Высокое p-value (обычно > 0.05): «Хм, вполне вероятно, что это просто случайное совпадение». У нас нет достаточных оснований, чтобы отвергнуть нулевую гипотезу. Мы не можем утверждать, что нашли реальный эффект. Результат статистически не значим.
Откуда взялось число 0.05? Это уровень значимости (альфа, α) — порог, который мы устанавливаем заранее. Это наша «планка для доказательств». Чаще всего используют α = 0.05 (или 5%), но в зависимости от задачи (например, в медицине) он может быть и 0.01.
Процесс принятия решения можно представить так:
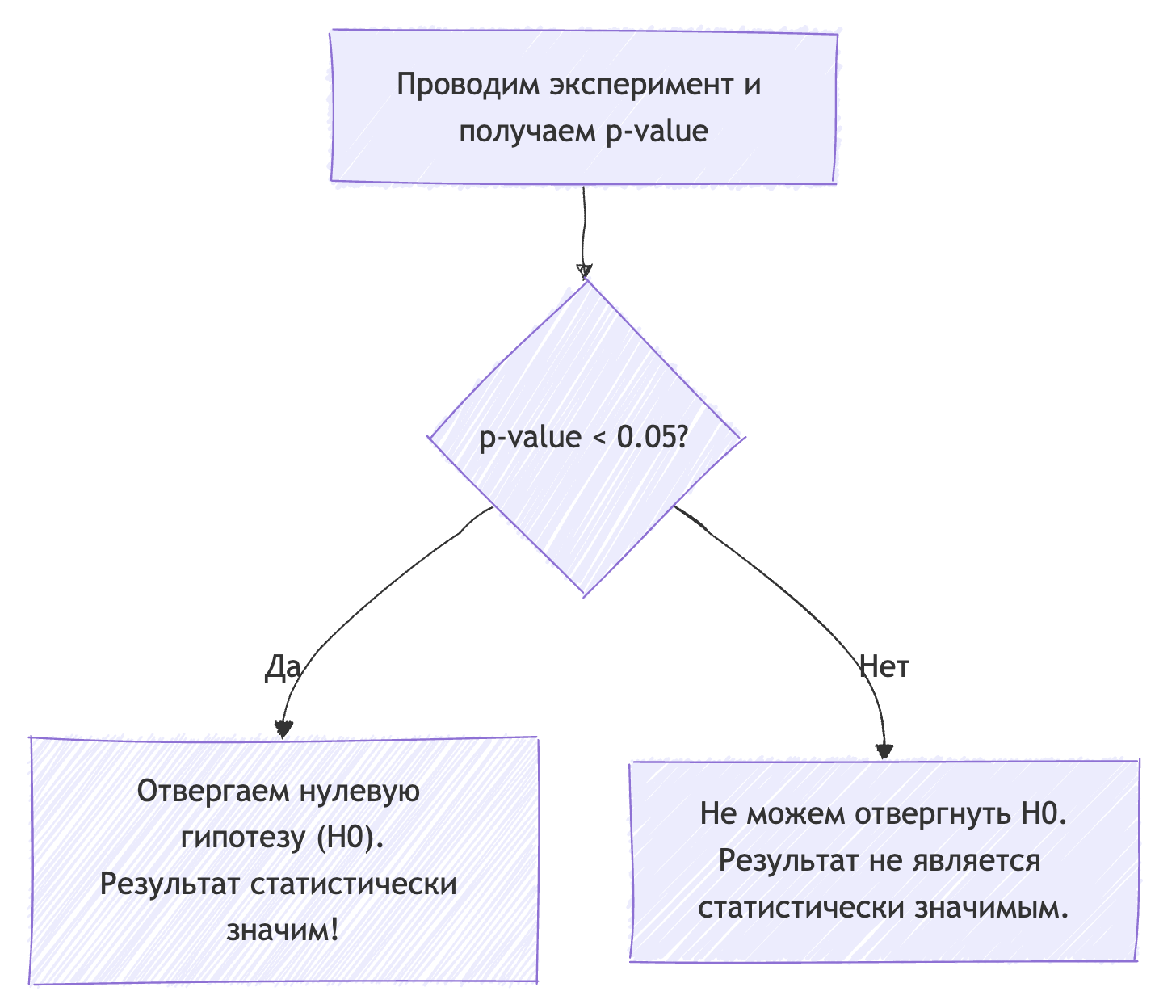
Практические примеры из мира Машинного обучения
Теория — это хорошо, но давайте посмотрим, как это работает на практике.
Пример 1: A/B тестирование новой кнопки на сайте
Задача: Команда маркетинга считает, что если перекрасить кнопку «Купить» из синей в зеленую, конверсия вырастет. Мы хотим это проверить.
Нулевая гипотеза (H0): Цвет кнопки не влияет на конверсию (CTR). Любая разница, которую мы увидим, — это случайность. CTR_зеленой = CTR_синей.
Альтернативная гипотеза (H1): Цвет кнопки влияет на конверсию. CTR_зеленой ≠ CTR_синей.
Действие: Мы запускаем A/B тест. 50% пользователей видят старую синюю кнопку (контрольная группа), а другие 50% — новую зеленую (тестовая группа). Собираем данные за неделю: количество показов и кликов для каждой версии. С помощью статистического теста (например, Z-теста для пропорций) мы вычисляем p-value.
Результат 1: p-value = 0.02
Интерпретация: 0.02 < 0.05. Это значит, что если бы цвет кнопки на самом деле ни на что не влиял, шанс увидеть такую (или большую) разницу в кликах был бы всего 2%. Это очень маловероятно!
Вывод: Мы отвергаем нулевую гипотезу. У нас есть статистически значимые доказательства, что зеленая кнопка работает иначе (скорее всего, лучше, если ее CTR выше). Можно смело выкатывать на всех!
Результат 2: p-value = 0.35
Интерпретация: 0.35 > 0.05. Это значит, что если бы цвет кнопки ни на что не влиял, шанс увидеть наблюдаемую разницу случайно составил бы целых 35%. Это вполне рядовое событие.
Вывод: Мы не можем отвергнуть нулевую гипотезу. У нас нет оснований утверждать, что зеленая кнопка лучше. Вероятно, небольшой рост, который мы увидели, был просто удачей. Внедрять изменение не стоит.
Пример 2: Оценка важности нового признака в модели
Задача: Мы строим модель для предсказания оттока клиентов. У нас возникла идея добавить новый признак: «количество обращений в техподдержку за последний месяц». Улучшит ли это нашу модель?
Нулевая гипотеза (H0): Новый признак не имеет значимой связи с оттоком. Улучшение метрик модели (если оно есть) — случайность. Коэффициент при этом признаке в модели равен нулю.
Альтернативная гипотеза (H1): Новый признак действительно помогает модели лучше предсказывать отток.
Действие: Мы обучаем модель (например, логистическую регрессию) с этим новым признаком. Многие библиотеки (например, statsmodels в Python) при обучении линейных моделей сразу рассчитывают p-value для коэффициента каждого признака.
Результат: Допустим, мы видим, что у нашего признака «количество обращений в поддержку» p-value = 0.001.
Интерпретация: Это значение намного меньше 0.05. Это говорит о том, что крайне маловероятно получить такую сильную связь между обращениями в поддержку и оттоком чисто случайно.
Вывод: Мы отвергаем H0. Признак статистически значим. Его определенно стоит оставить в модели, так как он несет в себе полезную информацию. Если бы p-value было, скажем, 0.5, это был бы кандидат на удаление, чтобы не усложнять модель без надобности.
Краткий итог: как это работает вместе?
Давайте соберем все в единый пошаговый алгоритм, ваш личный чек-лист для проверки идей.
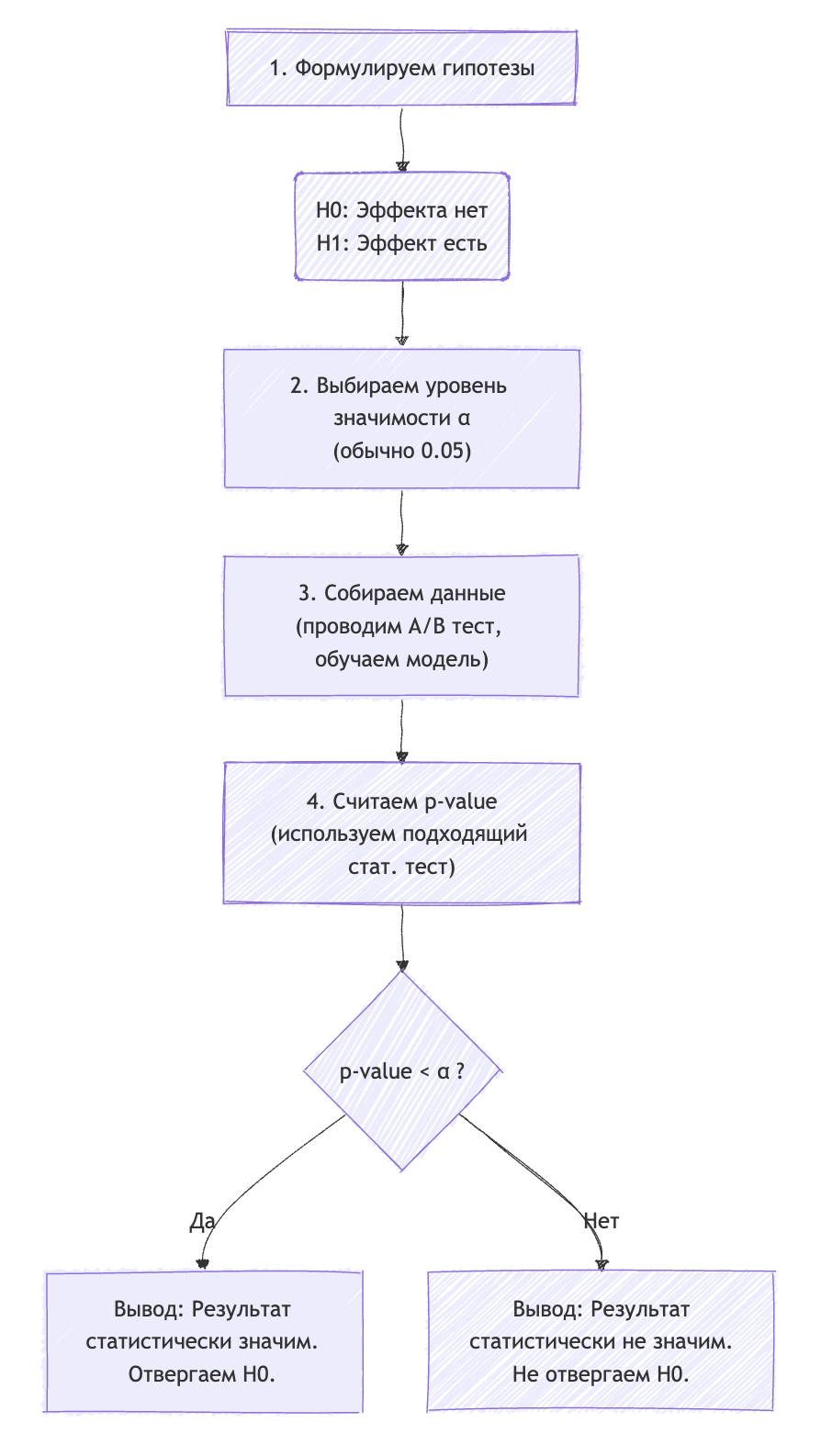
Статистическая значимость — ваш компас в мире данных
Как видите, в статистической значимости нет никакой черной магии. Это просто структурированный подход к проверке наших идей, который защищает нас от поспешных выводов.
Понимание этих принципов превращает вас из человека, который просто «обучает модельки», в специалиста, который может доказать ценность своих решений. Это помогает принимать взвешенные и обоснованные решения: стоит ли внедрять новую фичу, менять дизайн продукта или усложнять модель.
Для специалиста по машинному обучению статистическая значимость — это не просто теория из учебника, а ежедневный рабочий инструмент, который помогает отличать реальные закономерности от случайного шума. Используйте его, и ваши модели станут лучше, а решения — увереннее. Удачи в экспериментах!