Разбираемся, что такое убывающие и возрастающие функции, а также как решать задачи по определению промежутков монотонности функций при помощи производной.
Что такое функция
Функциями в математике называют зависимость значения одной величины от другой. Но функции часто встречаются и в окружающей нас жизни. Например, камень, брошенный под углом к горизонту, будет двигаться по параболической траектории. Космические аппараты на первой космической скорости движутся по круговой орбите, но при достижении второй космической их траектория становится параболической. При еще большем увеличении скорости космический аппарат начинает двигаться по гиперболе.
Во времена Второй мировой войны применяли специальные гиперболические системы для определения местоположения. Также всем известны параболические антенны для приема сигналов спутникового интернета и телевидения. Подобные антенны используются и для радиотелескопов, которые помогают астрофизикам изучать далекие космические объекты. Таких примеров можно привести множество, но вернемся к теории.
Всем известна формула для определения средней скорости:
То есть, чтобы узнать скорость, надо пройденный путь поделить на время, за которое этот путь был пройден. Другими словами, нам нужно знать две величины. Но если расстояние между двумя городами известно и равно, допустим, 60 километрам, то средняя скорость поезда будет зависеть только от времени:
График такой функции имеет следующий вид:
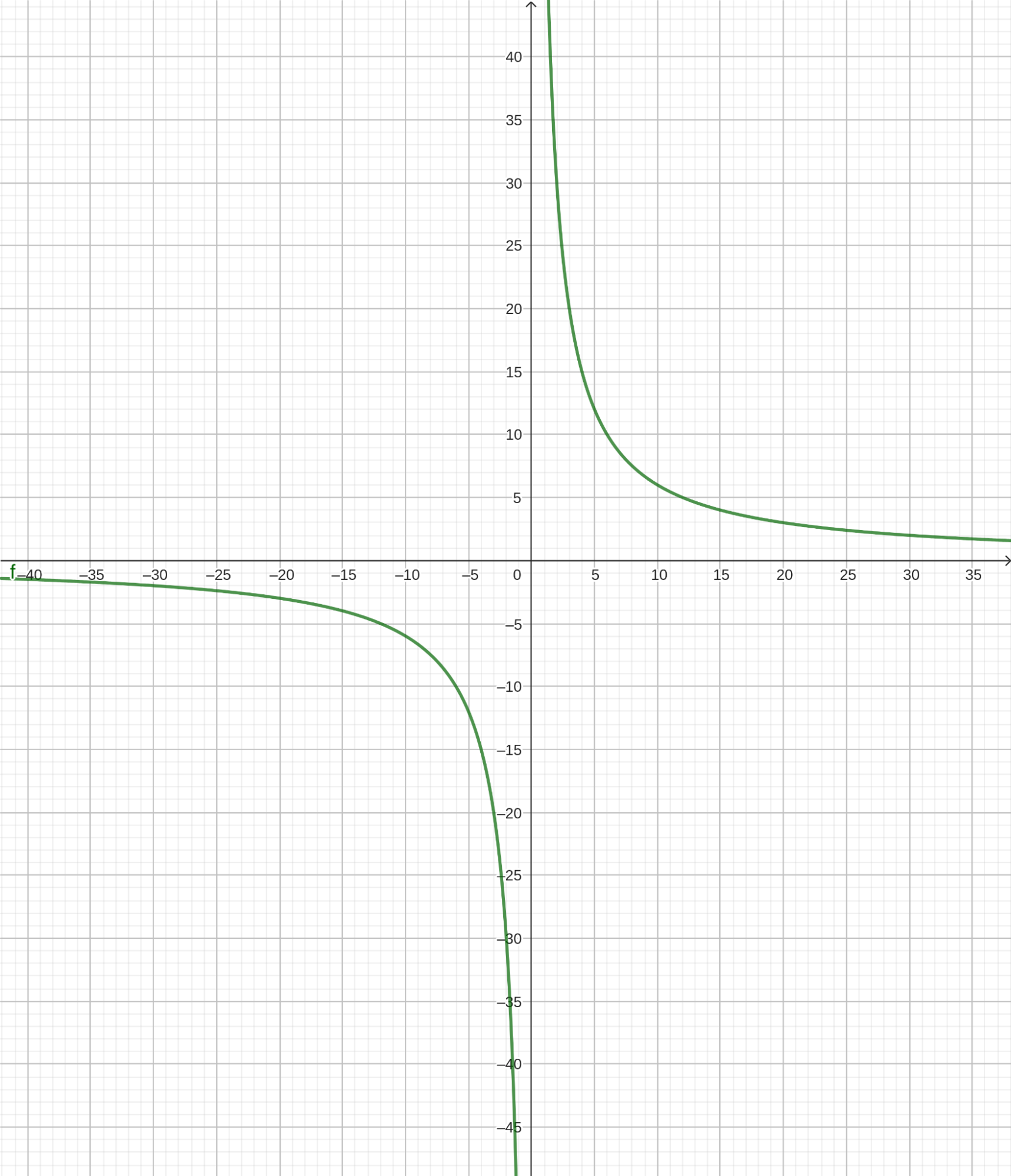
Такие функции называются обратными пропорциональностями. Переменная t — это независимая переменная, или, по-другому, аргумент. Все возможные значения аргумента составляют область определения функции. В нашем случае аргумент может принимать любые значения, кроме нуля. Это значит, что область определения нашей функции — вся числовая ось, за исключением начала координат. В начале координат находится точка разрыва функции.
Если есть обратные пропорциональности, то должны существовать и прямые пропорциональности. Так и есть! И в отличие от обратных они выглядят попроще. Ниже для примера приводится график такой функции \(f(x)=2x\):
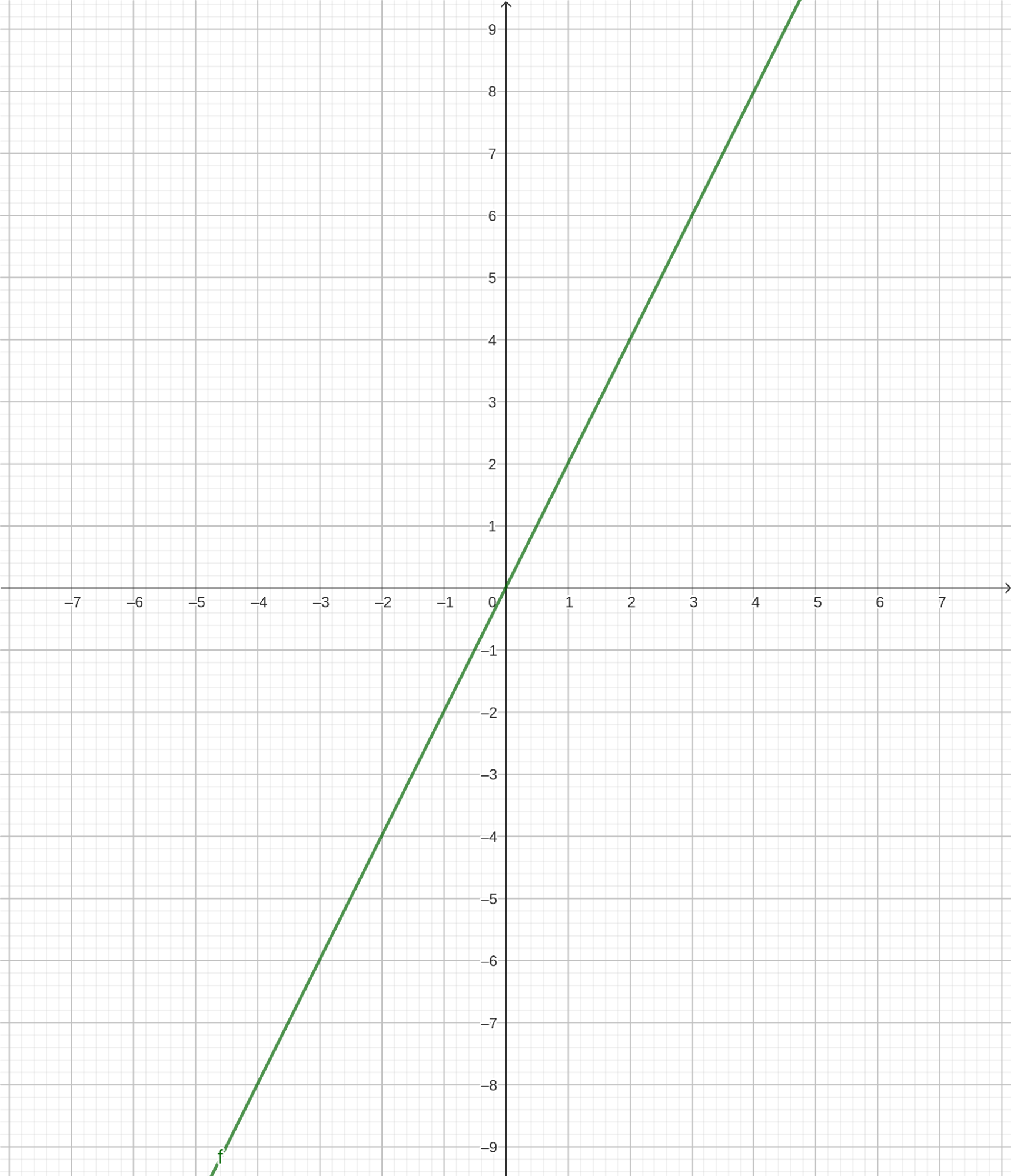
Как видно, это обычная прямая, проходящая через начало координат. Область определения и область значений этой функции — вся числовая ось. Никаких разрывов здесь нет. Такие функции называются непрерывными.
Прямая пропорциональность — это частный случай линейной функции, которая в общем виде может быть представлена формулой \(y=kx+b\), где для прямой пропорциональности \(b=0\). Из-за этого графики прямых пропорциональностей обязательно проходят через начало координат.
Важно запомнить, что не каждая кривая или прямая может являться графиком какой-либо функции. Функция — это такая зависимость одной переменной от другой, где каждому значению аргумента x соответствует единственное значение y. Например, окружность не может являться графиком функции, так как если провести через нее прямую, параллельную оси y, то она пересечет окружность в двух точках. Получается, что одному значению x соответствует два значения y, а это противоречит определению функции.
Возрастающие и убывающие функции
Функция называется возрастающей, если для каждого большего значения аргумента соответствует большее значение функции. И наоборот, функция называется убывающей, если для каждого большего значения аргумента соответствует меньшее значение функции. Так, приведенный выше пример прямой пропорциональности представляет собой возрастающую функцию, а пример обратной пропорциональности — это убывающая функция.
График обратной пропорциональности — это гипербола, которая состоит из двух ветвей. Соответственно, промежутков (интервалов) убывания у этой функции два: \((−∞,0)\) и \((0,+∞)\). Такие промежутки называют еще промежутками монотонности. Прямая пропорциональность возрастает на всей числовой прямой. То есть она является монотонной функцией, но бывают функции, которые на одних промежутках убывают, а на других возрастают. Такие функции называются немонотонными. Пример такой функции — \(f(x)=x^2\) . Ее график выглядит таким образом:
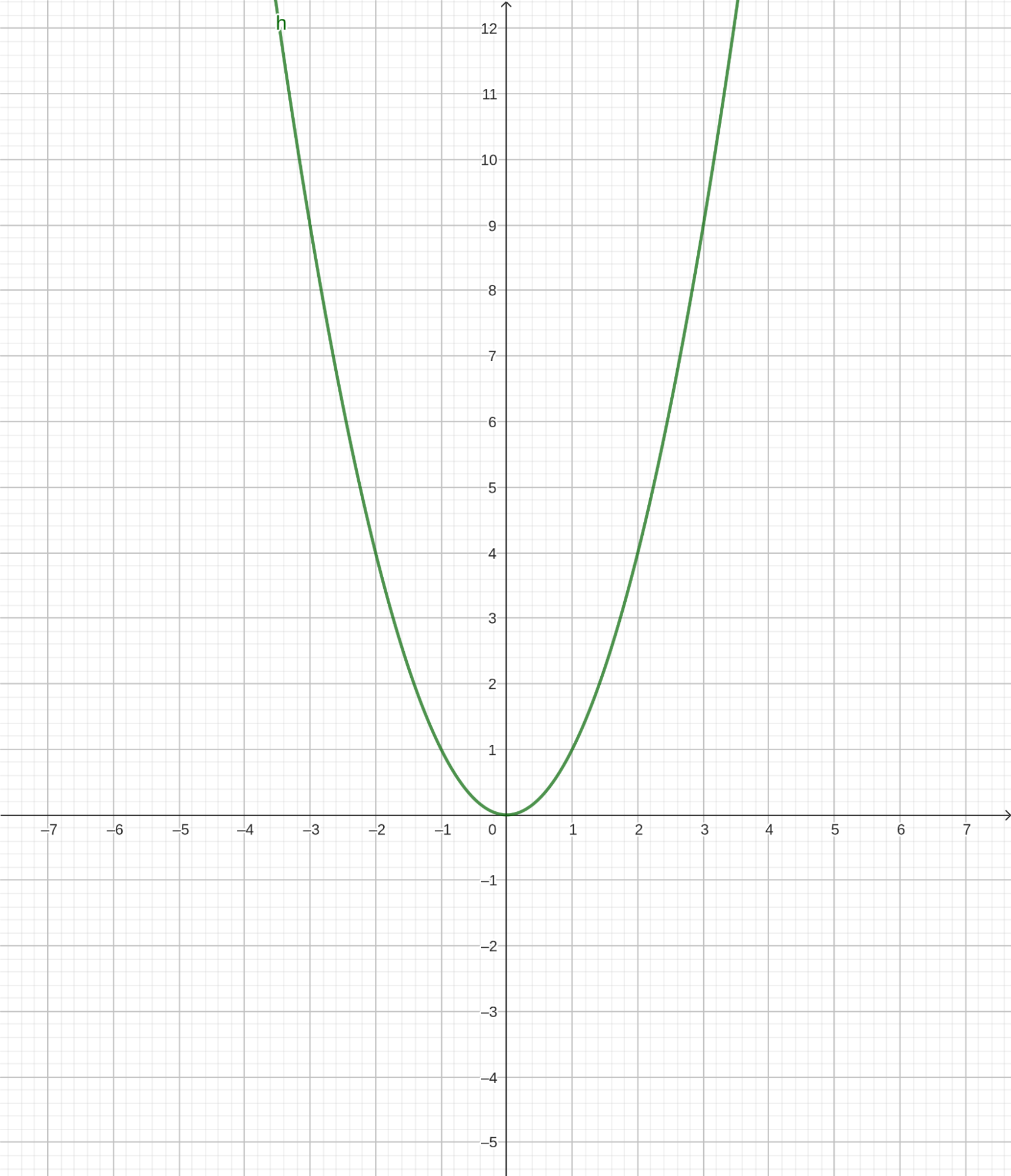
Такая кривая называется параболой. Как видно, здесь два промежутка монотонности. На промежутке от минус бесконечности до нуля функция является убывающей, а на промежутке от нуля до плюс бесконечности функция возрастает. Точка с координатами (0,0), которая является вершиной параболы, также является точкой минимума. В ней убывание функции сменяется возрастанием. Если в подобной точке происходит обратный процесс, то есть, наоборот, возрастание сменяется убыванием, то это точка максимума. Общее название для таких точек — точки экстремума.
Определить промежутки монотонности функции можно при помощи производной.
Что такое производная
Понятие производной очень важное в математике. При помощи производной можно произвести полное исследование функции и в том числе определить ее промежутки монотонности. Под производной понимается предел, к которому стремится отношение приращения функции к вызвавшему его приращению аргумента, когда последний стремится к нулю. То есть производная по сути характеризует скорость изменения функции.
Для вычисления производной степенной функции применяется следующая формула:
Для примера вычислим производную следующей функции:
Здесь следует учитывать, что производная суммы равна сумме производных и то, что производная постоянной величины равна нулю. Применяя формулу для степенной функции и учитывая все вышесказанное, получаем:
Приведем еще один пример. Найдем производную функции \(\frac{x^2-x} {x^4+5}\). Здесь нужно руководствоваться следующей формулой для вычисления производной дроби:
\((\frac{f}{g})’=\frac{f’g-fg’}{g^2}\), где \(g(x) \neq 0\)
То есть сначала перемножаем производную числителя со знаменателем. Потом из получившегося произведения вычитаем произведение числителя и производной знаменателя. На последнем этапе делим это все на квадрат знаменателя. Применяем формулу и получаем:
Теперь поговорим о применении производной в области нахождения промежутков монотонности функций.
Как найти промежутки монотонности
Покажем на простом примере, как находить такие промежутки. Найдем промежутки возрастания и убывания для функции \(x^3-12^x+2\). Производная данной функции равна \(3x^2-12\). Чтобы найти промежутки возрастания функции, надо найти промежутки, где ее производная положительна, то есть решить неравенство \(3x^2-12>0\). Разложив левую часть на множители, приведем неравенство к следующему виду:
Приравняем левую часть неравенства к нулю, так как производная в точках экстремума равна нулю либо вообще не существует. Получим уравнение \(3(x-2)(x+2)=0\). Как видно, корнями этого уравнения являются числа 2 и -2. Следовательно, множеством решений неравенства будут промежутки \((-∞,-2)\) и \((2,+∞)\). Отсюда делаем вывод: функция возрастает на промежутках \((-∞,-2)\) и \((2,+∞)\) и убывает на промежутке (−2,2). Это значит, что в точке \(x=-2\) функция имеет максимум, а в точке \(x=2\) — минимум. График подтверждает все наши вычисления:
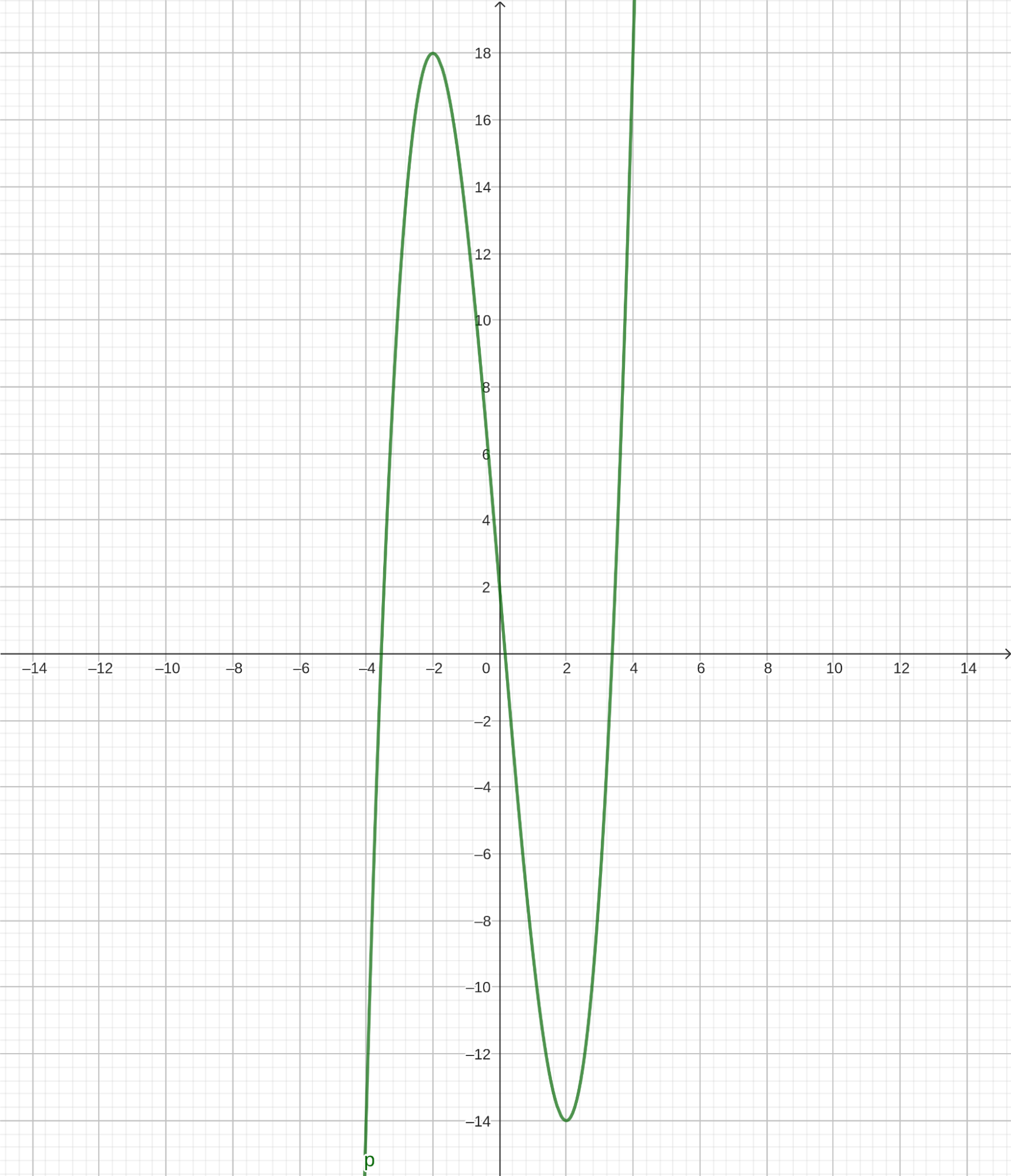
Как видим, все довольно просто! Решим еще одну задачу. Докажем, что 2 является точкой минимума функции \((x-2)^4\). Производная этой функции равна \(4(x-2)^3\). При \(x<2\) имеем: \(x-2<0\) и поэтому \(4(x-2)^3<0\). При \(x>2\) имеем: \(x-2>0\) и поэтому \(4(x-2)^3>0\). Значит, при переходе через точку 2 производная меняет знак с минуса на плюс, то есть сначала убывает, а потом начинает возрастать. Также функция в этой точке непрерывна, а следовательно, это точка минимума. Ниже показан график этой функции:
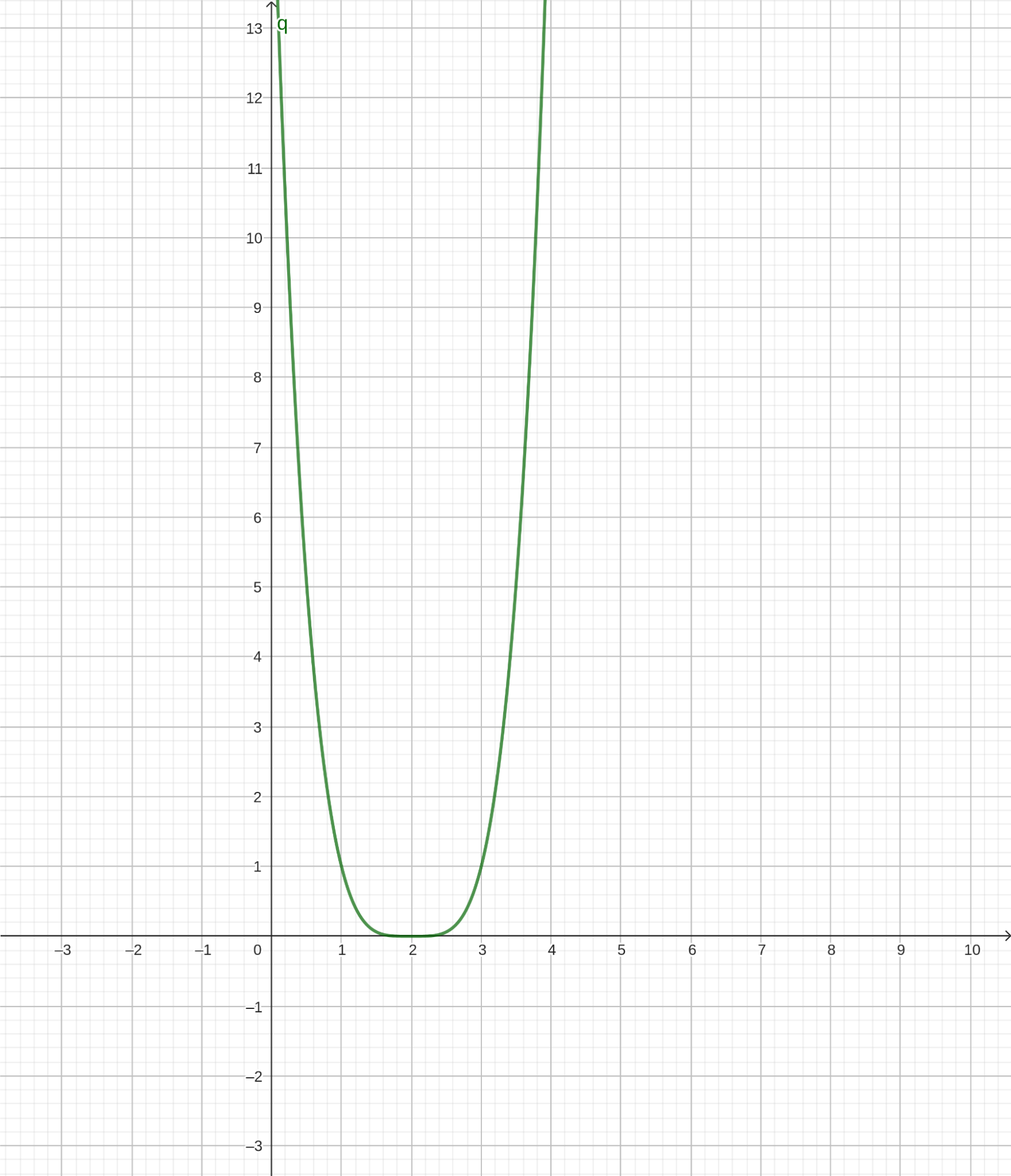
Далее разберем пример решения задачи на нахождение наибольшего значения функции.
Решаем задачу о прямоугольнике
Найдем прямоугольник наибольшей площади, вписанный в окружность радиуса R. Обозначим длины сторон прямоугольника через x и y:
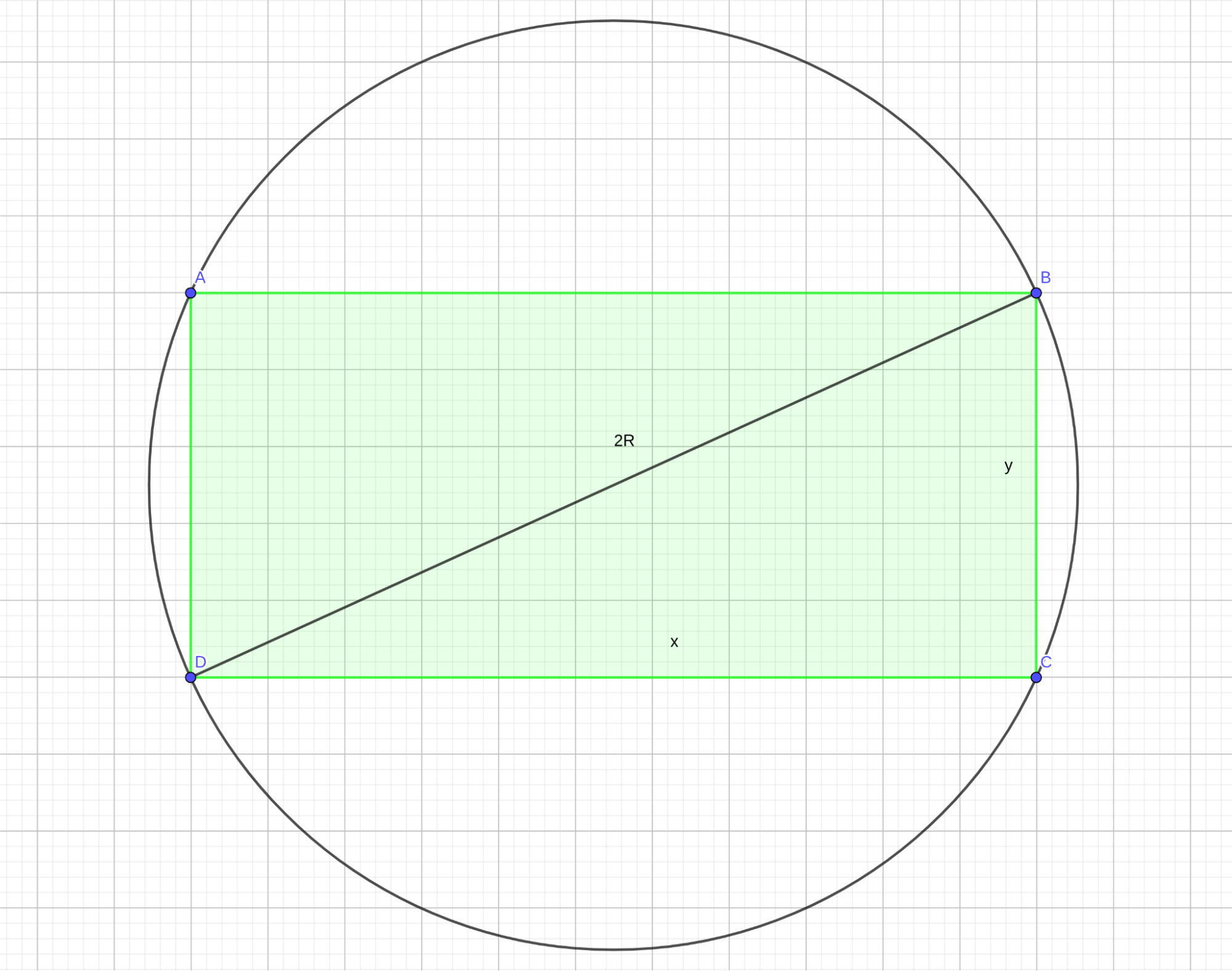
Тогда по теореме Пифагора выходит, что \(y=\sqrt {4R^2-x^2}\) и потому площадь S=xy выражается через x формулой \(S=x \sqrt {4R^2-x^2}\). Возведем обе части этой формулы в квадрат:
Таким образом мы избавились от радикала (корня). Производная функции \(4R^2x^2-x^4\) равна \(8R^2x-4x^3\). Вынесем общий множитель 4x за скобку и приравняем производную к нулю. Получим уравнение \(4x(2R^2-x^2)=0\), корнями которого являются числа 0, \(R\sqrt2\) и \(-R\sqrt2\).
Из них отрезку [0,2R] принадлежат 0 и \(R\sqrt2\). Поэтому надо сравнить значения функции \(4x(2R^2-x^2)\) в точках 0, \(R\sqrt2\) и 2R. При x=0 и x=2R функция обращается в нуль. Значит она принимает наибольшее значение при \(x=R\sqrt2\). В этом случае \(y=\sqrt{4R^2-(R\sqrt2)^2}=R\sqrt2\) и потому x=y. Другими словами, прямоугольником наибольшей площади, вписанным в окружность радиуса R, является квадрат.
Полезные ссылки
Математика с нуля — пошаговое изучение математики для начинающих.
Школьная математика — решение задач для начальной, средней и старшей школы.
Математическое образование — общедоступная электронная библиотека.
Математическая энциклопедия — можно найти толкование любого термина или понятия.








