Алгоритм k-means и метод локтя: кластеризация данных с примерами на Python

Кластеризация данных — одна из ключевых задач машинного обучения. Она позволяет группировать объекты в однородные кластеры на основе их характеристик. Один из самых популярных, простых и эффективных методов кластеризации — это алгоритм k-means. 

Рассмотрим, как работает k-means, познакомимся с методом локтя для определения числа кластеров и проиллюстрируем их применение на реальных данных с помощью языка программирования Python.

Что такое алгоритм k-means и как он работает

Алгоритм k-means используют для группировки объектов в наборы (кластеры) на основе их схожести. В основе работы k-means лежит принцип минимизации расстояния между объектами внутри одного кластера.

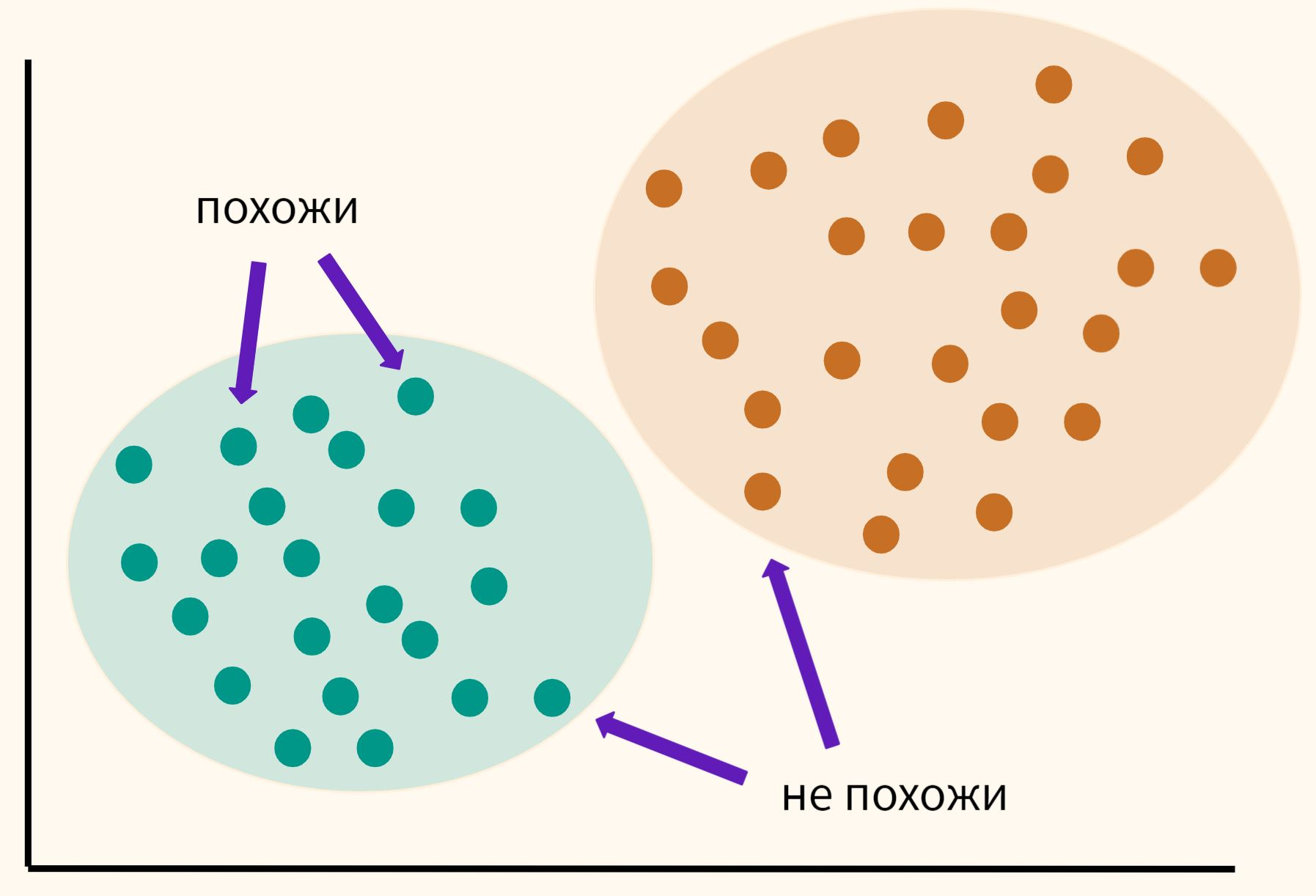
Представьте, что у вас есть много разноцветных шариков. Вам нужно разделить их на несколько групп, чтобы каждый шарик в группе был похож на остальные. Алгоритм помогает найти, как лучше всего сгруппировать эти шарики, чтобы в каждой группе они были максимально похожи друг на друга.

Он работает следующим образом: сначала выбираются несколько центров для групп (например, для трех групп — три центра). Затем алгоритм распределяет все шарики по группам, определяя, к какому центру они ближе. После этого он пересчитывает центры для новых групп и повторяет процесс, пока центры не перестанут сильно меняться. Это позволяет создать группы с шариками, схожими между собой.

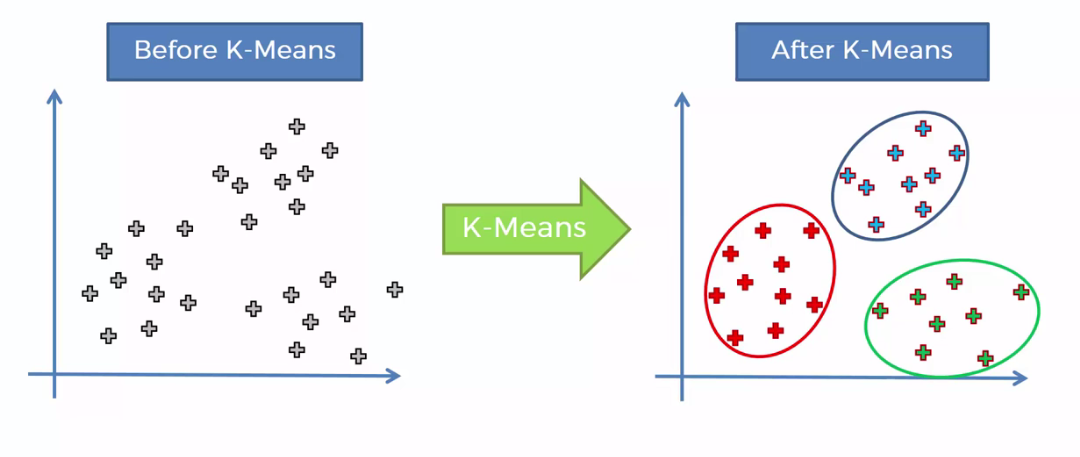
Основные этапы работы алгоритма k-means

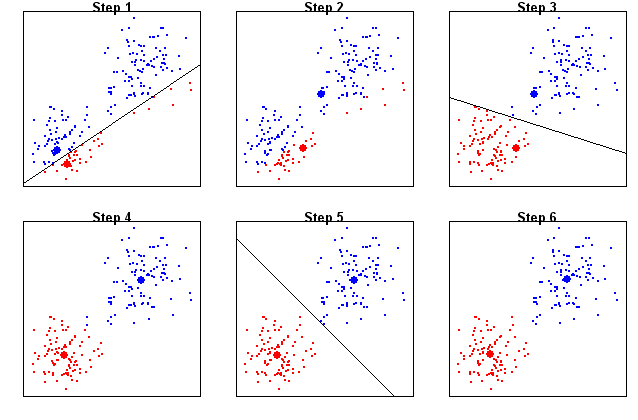
Алгоритм k-means можно описать в несколько шагов:

1. Выбор числа кластеров (k). На первом этапе необходимо определить количество кластеров, на которые будут разделены данные. Этот параметр задают вручную, и его правильный выбор напрямую влияет на качество кластеризации.
2. Инициализация центроидов. Алгоритм случайным образом выбирает k начальных точек, называемых центроидами. Эти точки служат временными центрами кластеров.
3. Назначение объектов кластерам. Каждый объект в наборе данных назначается к кластеру, центроид которого находится ближе всего. Для расчета расстояния обычно используют евклидову метрику, но есть и другие меры сходства, например косинусное расстояние или расстояние Манхэттена.
4. Обновление центроидов. После назначения объектов кластерам вычисляют новые центроиды. Каждый центроид перемещается в среднюю точку всех объектов, принадлежащих его кластеру.
5. Повторение. Шаги 3 и 4 повторяют до тех пор, пока центроиды не перестанут значительно изменяться, что свидетельствует о достижении сходимости. В некоторых реализациях алгоритм также может быть завершен при достижении заданного числа итераций.

Преимущества и недостатки k-means

Преимущества

1. Простота и быстрота реализации.
2. Эффективность при работе с большими наборами данных.
3. Возможность применения в различных областях, таких как сегментация клиентов, обработка изображений, анализ социальных сетей и другие.

Недостатки

1. Зависимость от выбора числа кластеров (k).
2. Чувствительность к начальной инициализации центроидов. Различные начальные точки могут привести к различным результатам.
3. Плохо справляется с данными, содержащими выбросы или сложные формы кластеров, например с перекрывающимися или нелинейными кластерами.
4. Не подходит для категориальных данных без предварительного преобразования.

Что такое метод локтя или как выбрать оптимальное число кластеров

Один из самых сложных этапов алгоритма k-means — выбор оптимального числа кластеров k. Если значение k слишком маленькое, то в одном кластере могут оказаться слишком разные объекты, что ухудшит качество кластеризации. Если значение k слишком большое, кластеры могут стать слишком мелкими и специфичными, что также приведет к плохим результатам. Чтобы выбрать оптимальное число кластеров, можно использовать несколько методов, и один из самых популярных — метод локтя.

Метод локтя: принцип работы

Метод локтя заключается в следующем: мы выполняем кластеризацию для различных значений k и строим график зависимости суммарной внутрикластерной дисперсии от количества кластеров. Внутрикластерная дисперсия (или сумма квадратов расстояний между объектами и их центроидом) показывает, насколько компактными являются кластеры. Чем меньше внутрикластерная дисперсия, тем более «упорядочены» и «однородны» кластеры.

Чтобы применить метод локтя:

1. Запускаем алгоритм k-means для разных значений kkk, например от 1 до 10.
2. Вычисляем внутрикластерную дисперсию для каждого значения kkk. Это можно сделать с помощью метрики, которая рассчитывает сумму квадратов расстояний между точками данных и центроидом их кластера.
3. Строим график: на оси X откладываем значения kkk, а на оси Y — соответствующие значения внутрикластерной дисперсии.
4. Ищем «локоть» на графике: это точка, где дальнейшее увеличение числа кластеров не приводит к значительному снижению внутрикластерной дисперсии.

Точка на графике, где происходит значительное снижение дисперсии, а затем снижение становится менее заметным, называется локтем. Это и есть оптимальное количество кластеров.

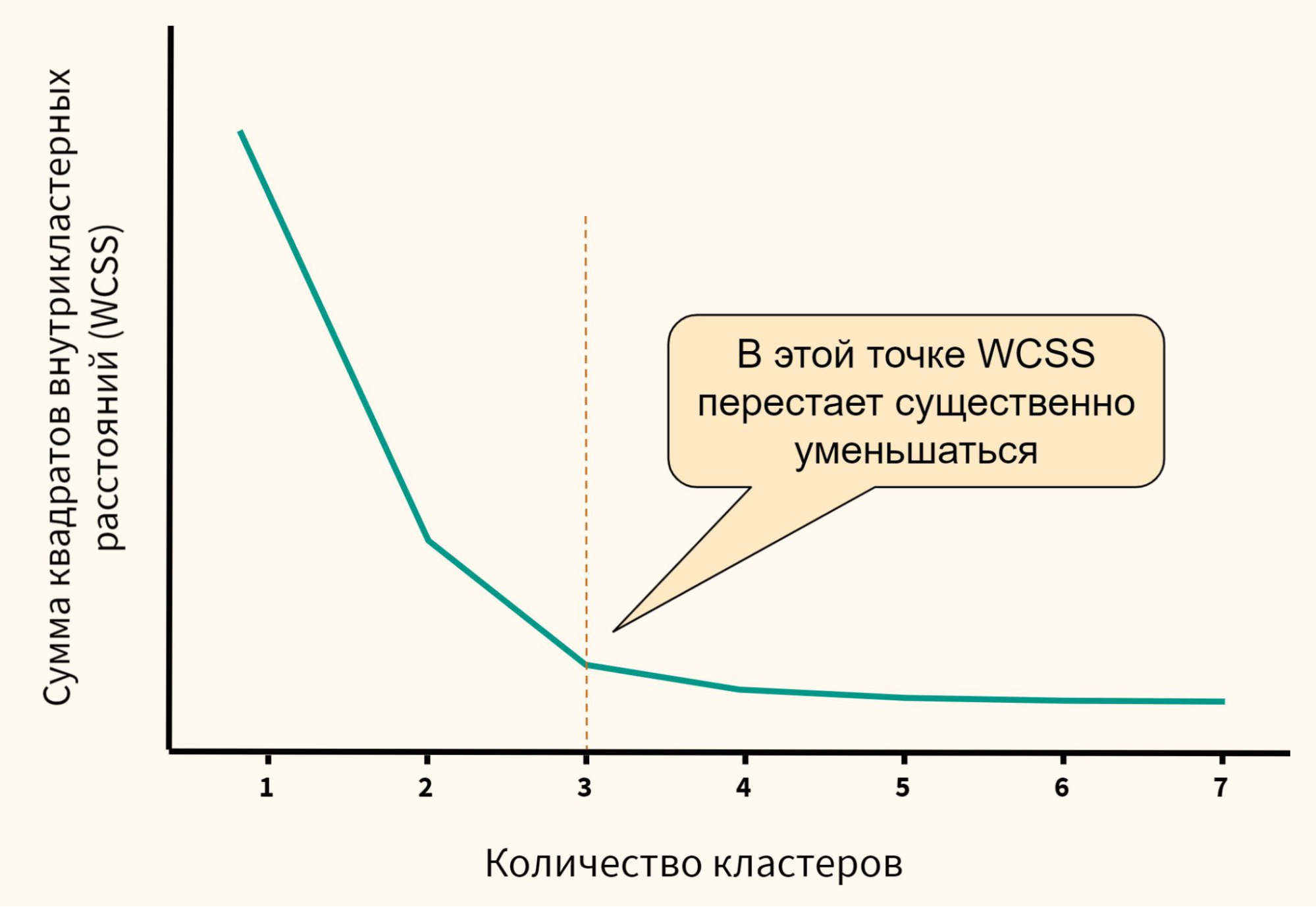
Почему метод называется «метод локтя»?

Название метода происходит от формы графика, получаемого в процессе его применения. Если на графике отложены значения k и внутрикластерной дисперсии, то график будет выглядеть как угловатая линия, которая резко падает до определенной точки, а затем продолжает снижаться, но уже не так сильно. Этот угол, напоминающий локоть, и является тем самым «локтем», который мы ищем.

Недостатки метода локтя

Несмотря на свою популярность и простоту, метод локтя имеет несколько ограничений:

• Сложность в интерпретации. В некоторых случаях на графике может быть несколько «локтей», что затрудняет выбор оптимального числа кластеров.
• Зависимость от данных. Метод локтя может не работать хорошо для данных с очень сложной структурой или с высокой размерностью.
• Предположение о формах кластеров. Метод локтя предполагает, что кластеры будут иметь компактную форму и схожие размеры. В обратном случае метод может не дать корректного ответа.

Другие методы выбора числа кластеров

Помимо метода локтя, существуют и другие подходы для выбора оптимального числа кластеров:

• Метод силуэта измеряет, насколько хорошо объекты могут быть разделены на кластеры. Чем выше значение силуэта, тем лучше объект вписывается в свой кластер.
• Метод gap statistic сравнивает внутреннюю дисперсию кластеров с дисперсией кластеров, полученных на случайных данных. Это помогает выбрать оптимальное количество кластеров.
• Иерархическая кластеризация не требует заранее заданного числа кластеров и помогает понять, сколько кластеров лучше всего соответствует данным.

Как написать кластеризацию методом k-средних на Python

Шаг 1. Установка библиотек

Для начала убедитесь, что у вас установлены необходимые библиотеки. Мы будем использовать NumPy, Matplotlib и scikit-learn для кластеризации и визуализации данных. Установить их можно с помощью команды:

pip install numpy matplotlib scikit-learn

Шаг 2. Импортирование библиотек

Для начала импортируем необходимые библиотеки:

import numpy as np

import matplotlib.pyplot as plt

from sklearn.cluster import KMeans

• NumPy используется для работы с массивами данных.
• Matplotlib поможет визуализировать результаты.
• KMeans — это класс из библиотеки scikit-learn, который реализует алгоритм k-средних.

Шаг 3. Создание данных

Для этого примера мы создадим простые данные, которые будем кластеризовать. В реальной жизни данные могут поступать из разных источников (например, CSV-файлы, базы данных), но для удобства здесь мы сгенерируем данные с помощью NumPy:

# Генерация случайных данных

np.random.seed(42)

# Создаем 2D-данные: 300 объектов, 2 признака

X = np.concatenate([np.random.normal(loc=-2, scale=1, size=(100, 2)),

                   np.random.normal(loc=3, scale=1, size=(100, 2)),

                   np.random.normal(loc=7, scale=1, size=(100, 2))])

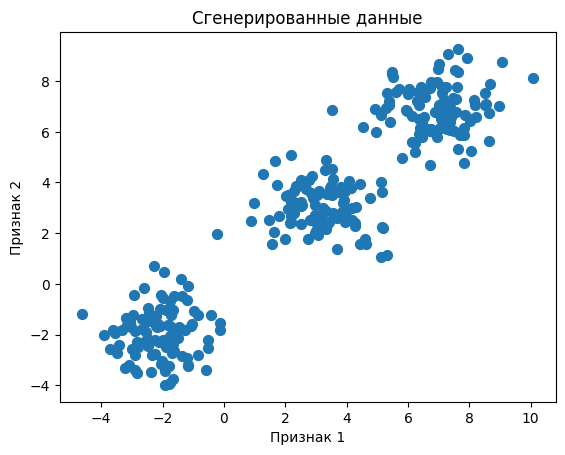
# Визуализируем сгенерированные данные

plt.scatter(X[:, 0], X[:, 1], s=50, cmap='viridis')

plt.title("Сгенерированные данные")

plt.xlabel("Признак 1")

plt.ylabel("Признак 2")

plt.show()

Этот код генерирует 300 точек данных, разделенных на три группы с различными средними значениями и стандартными отклонениями. После генерации данных мы визуализируем их, чтобы увидеть, как они распределены.

Шаг 4. Применение метода k-средних

Теперь, когда у нас есть данные, применим алгоритм k-средних для их кластеризации. Мы будем использовать три кластера, так как мы знаем, что данные были сгенерированы с тремя центрами.

# Применяем k-средних с 3 кластерами

kmeans = KMeans(n_clusters=3)

kmeans.fit(X)

# Получаем результаты кластеризации

labels = kmeans.labels_ # Массив меток кластеров

centroids = kmeans.cluster_centers_ # Центры кластеров

В этом коде:

• n_clusters=3 указывает, что мы хотим разделить данные на три кластера.
• Метод fit() обучает модель, а labels_ возвращает массив меток для каждого объекта, указывающих, в какой кластер он был отнесен.
• cluster_centers_ содержит координаты центров кластеров.

Шаг 5. Визуализация результатов

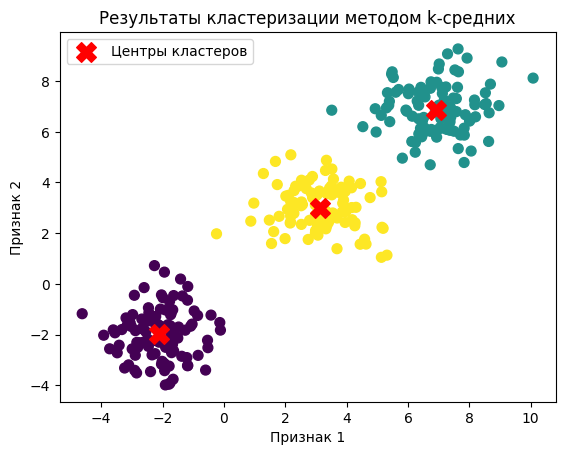
После того как модель обучена, можно визуализировать результаты кластеризации. Мы покажем данные и центры кластеров на графике:

plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')

plt.scatter(centroids[:, 0], centroids[:, 1], c='red', s=200, marker='X', label='Центры кластеров')

plt.title("Результаты кластеризации методом k-средних")

plt.xlabel("Признак 1")

plt.ylabel("Признак 2")

plt.legend()

plt.show()

Здесь:

• Мы визуализируем данные, раскрашенные по кластерам (с помощью c=labels).
• Центры кластеров отображаются красными крестами.

Шаг 6. Оценка качества кластеризации (метод локтя)

Для того чтобы определить оптимальное количество кластеров для ваших данных, можно использовать метод локтя. Мы будем строить график зависимости суммы внутрикластерных расстояний от числа кластеров и искать точку, где этот график начинает «выпрямляться».

# Метод локтя: вычисление внутрикластерных расстояний для разных значений k

inertia = []

for k in range(1, 11):

    kmeans = KMeans(n_clusters=k)

    kmeans.fit(X)

    inertia.append(kmeans.inertia_)

# Строим график

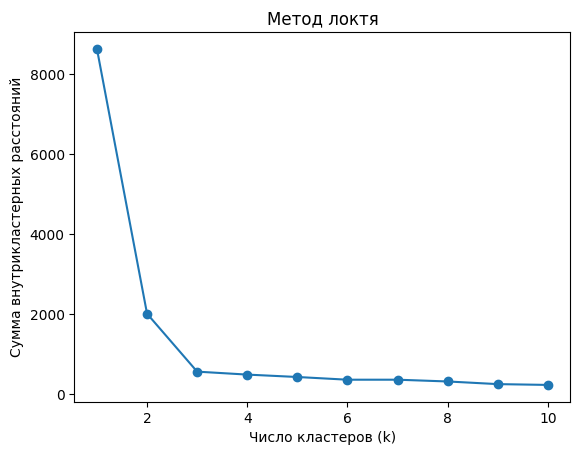
plt.plot(range(1, 11), inertia, marker='o')

plt.title("Метод локтя")

plt.xlabel("Число кластеров (k)")

plt.ylabel("Сумма внутрикластерных расстояний")

plt.show()

Здесь:

• inertia_ — это сумма квадратов расстояний между объектами и их центроидом, то есть внутрикластерная дисперсия.
• Мы вычисляем инерцию для разных значений kkk и строим график.

На графике вы должны увидеть точку «локтя», где добавление новых кластеров перестает значительно уменьшать внутрикластерное расстояние.

Шаг 7. Выбор оптимального числа кластеров

Как только вы найдете точку локтя, это будет наилучшее количество кластеров для ваших данных. Например, если на графике видно, что инерция начинает уменьшаться значительно медленнее после k = 3, то это значит, что оптимальное число кластеров для вашего набора данных — три.

А такие графики получились:

Где используют алгоритм k-means в реальной практике

Алгоритм k-средних (k-means) используют во многих областях для решения задач, связанных с кластеризацией данных. Вот несколько примеров применения на практике:

• Обработка изображений

K-средних часто используется для сегментации изображений. Например, для разделения изображения на несколько частей (для выделения объектов или текстур). Это может быть полезно в компьютерном зрении для распознавания объектов, фильтрации шума или анализа медицинских изображений.

• Анализ текстов

В обработке естественного языка (NLP) k-средних используют для кластеризации текстов. Это помогает группировать документы, статьи или сообщения, которые имеют схожую тему, тональность или содержание. Применяется в системах рекомендаций, например в новостных агрегаторах или системах поиска.

• Обнаружение аномалий

Алгоритм k-средних используют для выявления аномальных или подозрительных данных, которые не соответствуют ожидаемым паттернам. Это важно для системы мониторинга безопасности или анализа финансовых транзакций.

• Рекомендательные системы

k-средних помогает создавать рекомендательные системы, анализируя поведение пользователей и их предпочтения. Сегментирование пользователей в кластеры позволяет улучшить точность рекомендаций.