Дата-сайентисты, специалисты по машинному обучению и робототехнике много работают с математикой. Математические методы нужны для обработки информации, создания моделей и разработки эффективных алгоритмов. Но на старте обучения математика кажется магией, а в некоторых понятиях и вовсе легко запутаться.
Задача науки о данных — обрабатывать информацию. Есть набор данных, его нужно описать единой функцией и выявить закономерности. Но в наборах много шумов и колебаний, графики негладкие и нестабильные. Чтобы привести их к более понятному виду, существуют разнообразные численные методы.
Известные методы обработки данных — аппроксимация, интерполяция и экстраполяция. Названия методов звучат похоже. Но это разные вещи. Рассказываем, в чем их суть, чем они различаются и для чего нужны.
Аппроксимация. «Ближнее», как Проксима Центавра
Если говорить простыми словами, аппроксимация — это метод нахождения ближнего. Аппроксимировать — это заменить одни результаты другими, близкими к исходным, но упрощенными.
В математике это построение кривых, близких к имеющемуся набору значений. Представьте себе изменение показателя: оно строится по множеству найденных точек. Получается неровный, угловатый график, ведь при нахождении каждой точки были погрешности.
Например, точки — показания, снятые с какого-то датчика. На точность могут влиять помехи и разные шумы вокруг. Даже если результат двух измерений на самом деле одинаковый, датчик может выдать для них два разных результата из-за помех.
В таких ситуациях нужно сгладить график — найти средние значения, чтобы привести набор результатов к единой функции. Для этого существует аппроксимация функции.
Пример аппроксимации по точкам:
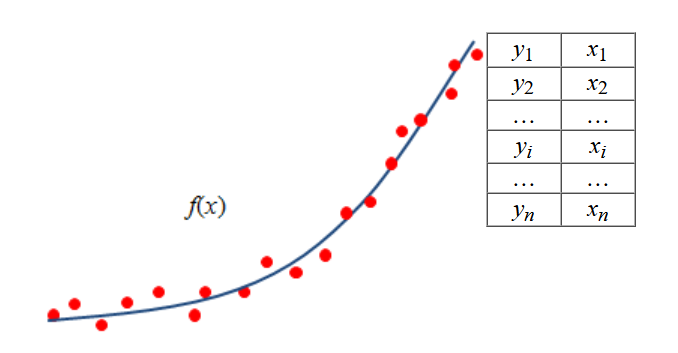
Красные точки на графике — найденные результаты. Они неоднородные, неровные, по ним не получится построить гладкую функцию. А синяя линия — линия аппроксимации. Она высчитана по аппроксимирующей функции f(x) и сделала результаты однороднее и проще для восприятия.
Зачем нужно. Компьютер может хранить данные со всеми неровностями и погрешностями, для него разницы нет. Но с информацией работает человек, а ему проще, когда набор данных можно описать функцией. Одна из задач науки о данных — прогнозирование. Если набор результатов можно описать функцией, прогнозировать легче.
Как связано с другими методами. Методы аппроксимации помогают интерполировать и экстраполировать данные; об этом расскажем ниже. Аппроксимация — общий термин: интерполяция и экстраполяция считаются ее подвидами.
Интерполяция. Как «интервал» — находится внутри
Интерполяция простыми словами — это нахождение неизвестных промежуточных значений с помощью нескольких известных. Интерполировать — это, по сути, вставить дополнительные значения в ряд.
Выше говорили, что график строится по множеству точек. Показатели невозможно отслеживать непрерывно, поэтому график получается дискретным. Например, нашли результаты в точке А и в точке Б. А что находится между ними — не знаем.
Когда это происходит, рассчитываем значения между А и Б как нечто среднее. Если в точке А значение 0, в точке Б — 1, а график на отрезке идет как прямая, то ровно между А и Б рассчитаем значение как 0,5. Это и есть интерполяция.
На этом графике красной точкой отмечен результат, полученный с помощью интерполирования:
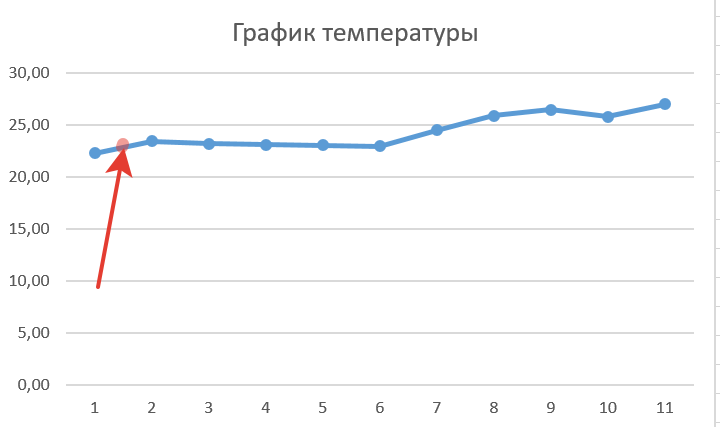
Мы знаем результаты в точках 1 и 2 — их называют базовыми точками, — но не знаем, что посередине. Используем в качестве интерполяционной функции уравнение прямой и получаем примерные значения, которые находятся между точками
Это один из наиболее простых вариантов, линейная интерполяция. Виды интерполяции разнообразны, многие из них сложные:
- для прямой интерполяции есть интерполяционные формулы Ньютона, сплайн-функции, интерполяционный многочлен Лагранжа и многое другое;
- существует обратная интерполяция — когда промежуточное значение известно, но нужно понять, где именно в промежутке оно находится;
- бывает интерполяция функции с несколькими переменными, например билинейная или бикубическая.
Зачем это нужно. Часто для точного расчета нужно иметь под рукой промежуточные данные. Разнообразные методы интерполяции помогают найти их и составить полную картину. Результат получается приближенным к реальности в зависимости от выбранного метода.
Как связано с другими методами. Интерполирование проще проводить на аппроксимированных кривых. Когда есть просто набор точек, который не описан функцией, очень сложно предугадать, что находится посередине. А если есть приблизительная функция, которая поясняет, как распределяются точки, легче предположить промежуточное значение.
Экстраполяция. Экстремально за пределами
Экстраполяция — это метод нахождения значений за пределами интервала. До этого мы искали промежуточные значения на графике. Теперь представим еще одну ситуацию. График заканчивается, мы узнали текущие значения, и надо предположить, какие значения этот же показатель будет принимать в будущем.
Получается задача прогнозирования, одна из ключевых в науке о данных. Для ее решения математика предлагает методы экстраполяции. Разница с интерполяцией в том, что неизвестные данные ищутся не в промежутке, а за его пределами.
Красные точки на графике высчитаны с помощью экстраполяции:
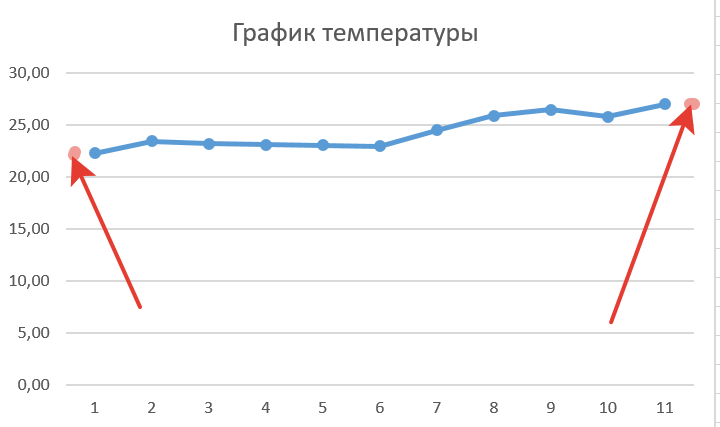
Мы не знаем, какими они были или будут на самом деле. Но можем рассчитать благодаря численным методам.
Как и в случае с интерполяцией, существует огромное количество методов для расчета. Некоторые из них дублируют интерполирующие методы. Например, популярный способ — параболическая экстраполяция, которую считают с помощью формул интерполяции.
Существует несколько основных стратегий экстраполяции:
- Экстраполяция на основе индукции (тенденциальная экстраполяция)основана на предположении, что существующие тенденции будут продолжаться в будущем. Например, если цены на что-то растут из года в год, можно предположить, что эта тенденция сохранится и дальше.
- Экстраполяция с применением аналогового моделирования использует похожие ситуации или модели для предсказания будущих событий. Например, есть данные о том, как развивались продажи похожего продукта в прошлом. Их можно использовать, чтобы предсказать, как будет продаваться новый продукт.
- Экстраполяция выборочных данных на всю генеральную совокупность. Метод предполагает, что можно сделать выводы о всей группе, изучив только ее часть. Например, провести опрос среди небольшой группы людей, соблюдая определенные правила. Затем использовать результаты, чтобы сделать выводы обо всей популяции.
Зачем это нужно. Для решения задачи прогнозирования и получения большего количества данных. И наоборот — для ретроспективного прогнозирования, чтобы понять примерные результаты из прошлого, еще до начала отслеживания.
Как связано с другими методами. Как и с интерполяцией, экстраполяцию удобнее проводить на аппроксимированных кривых. Для экстраполирования используются многие формулы и методы, которые обычно применяют при интерполяции данных.
А что еще? Другие численные методы
Коротко рассказали о сути аппроксимации, интерполяции и экстраполяции. Это довольно поверхностное описание, но важное для изучения более глубоких и конкретных понятий. Например, на практике используют такие численные методы, как:
- метод наименьших квадратов — для оценки неизвестных параметров на основе имеющихся;
- равномерное и среднеквадратичное приближение — для преобразования очень сложных функций в более простые, но приближенные к реальности;
- альтернанс Чебышева — один из способов приближения функций;
- алгоритм Ремеза — метод равномерной аппроксимации какой-то функции.
В зависимости от сложности задачи, могут встречаться разные способы приближения функций. Не всеми придется пользоваться постоянно, но иметь понимание нужно.
Еще одна важная деталь: рассчитанные таким образом значения имеют погрешность. Во многих случаях сложно сказать, какова величина ошибки. Поэтому обычно проверяют только то, насколько гладкими и логичными получаются итоговая функция и набор значений.