Числа с плавающей точкой: что это такое и как с ними работать

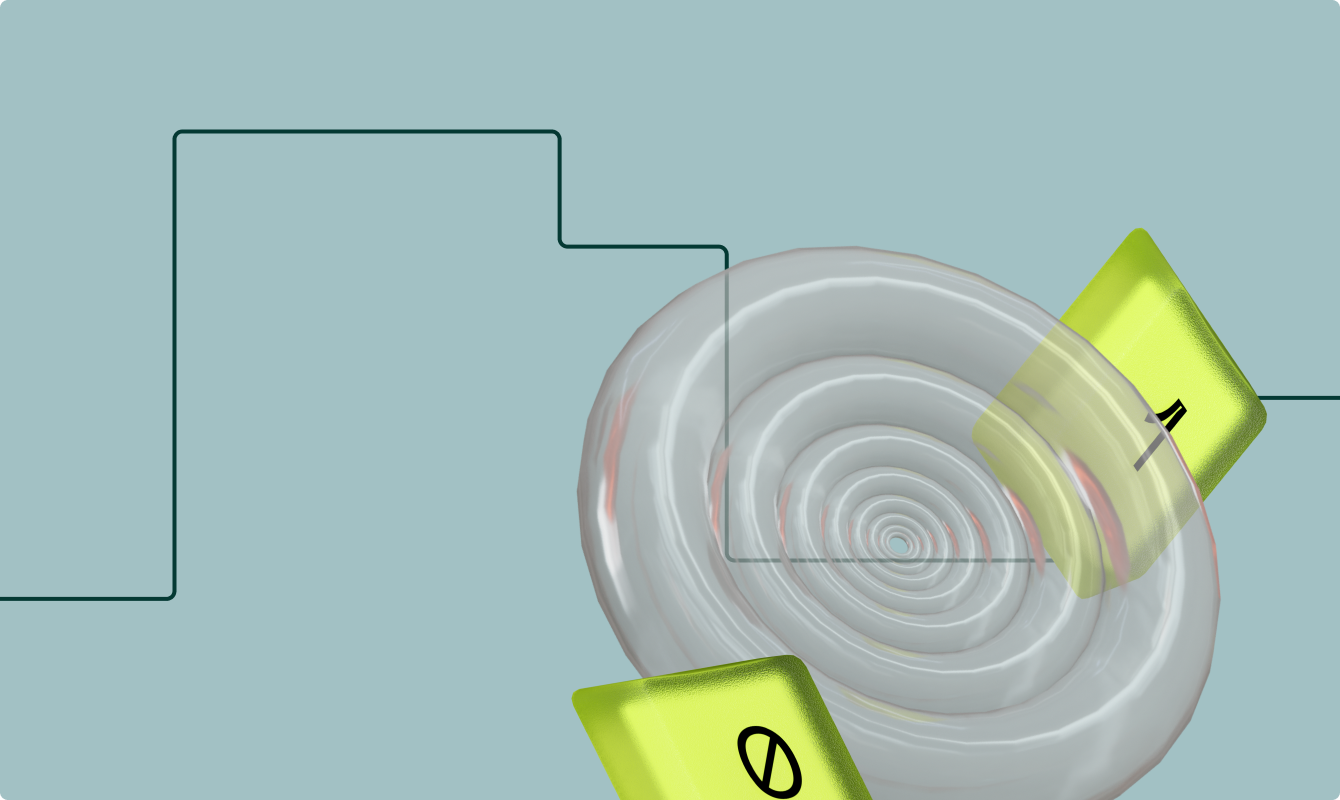
В разработке часто приходится иметь дело с вычислениями. А в вычислениях — с дробными числами. Несмотря на то что компьютерные расчеты ассоциируются с точностью, дроби — их слабое место. В памяти компьютера тяжело хранить нецелые числа.

Чтобы обойти эту проблему, придумали специальный формат хранения дробей — числа с плавающей запятой или точкой. Как устроен этот тип данных, в чем его особенности и как с ним работать, рассказали в статье.

В чем суть плавающей точки и зачем это нужно

Компьютеры проводят вычисления не так, как люди. Числа внутри них переводятся в двоичный формат, где каждое представлено в виде набора нулей и единиц. Но такой способ хранения не слишком удобен для дробей. Причина в том, как хранятся числа в памяти компьютера.

• Дробь состоит из целой и дробной части. Эти части нужно как-то хранить, при этом связывать друг с другом, а при вычислениях использовать вместе.
• Некоторые дроби вообще невозможно в точности представить на компьютере. Речь идет о бесконечных дробных числах вроде числа пи. Или о числах, где дробная часть — в периоде, например 3,333333… Приходится округлять такие дроби с определенной точностью.

Из-за этих особенностей вычисления дробей в прошлом веке были медленными и не всегда точными. Более того: каждый производитель представлял дробные числа по-своему, и переносить данные с одного компьютера на другой было тяжело. Что-то считывалось не так, а что-то терялось.

Чтобы разрешить проблему и более эффективно работать с дробями, для их записи и отображения в компьютерах придумали специальный стандарт: формат IEEE 754. Он закрепил понятие числа с плавающей точкой (float point). А еще — методы и принципы, по которым с этими числами работают компьютеры.

Как устроено число с плавающей точкой

Формат такого числа в большинстве языков программирования называется float — от английского слова «плавать». Число в этом формате состоит из трех частей: знакового бита, мантиссы и экспоненты.

• Знаковый бит — это один бит, который показывает, положительное число или отрицательное. В записи числа он идет самым первым.
• Мантисса числа — это постоянное количество бит, которое показывает точность числа. Она выглядит как число, в котором содержатся существующие в числе цифры.
• Экспонента числа — это показатель, на который нужно умножить мантиссу, чтобы получилось нужное число.

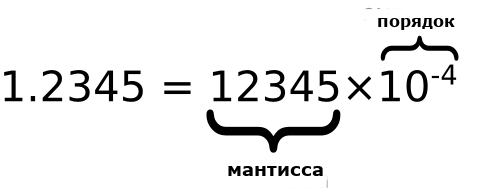
Этот принцип похож на то, как числа записывают ученые. Часто в учебниках математики можно встретить такой формат записи, как:

0,15 × 10^–3

Если представить записанное таким образом число в формате float, получится так:

• 0,15 — это мантисса. Она содержит значимые цифры числа.
• 10 — так называемое основание. Оно может быть и другим, но обычно используют 10, потому что десятичная система привычна для людей;
• –3 — экспонента. Она показывает, на какое число мы умножаем мантиссу.

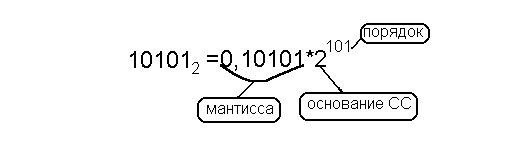
В этом примере число довольно легко перевести из научной нотации в float — оно изначально находится в диапазоне от 0 до 1. Но если оно больше 1, лучше немного его преобразовать.

Например, возьмем число 1,2 × 10^–3 . Коэффициент 1,2 не получится использовать как мантиссу: число больше 1. Значит, понадобится уменьшить его разрядность — разделить на 10. А чтобы число по-прежнему осталось верным, нужно преобразовать экспоненту. Получится так:

1,2 × 10^–3 = 0,12 × 10^–2

Оба варианта записи верны и указывают на одно и то же число: 0,0012. Разница только в том, что в float-формате все значимые цифры числа указываются в мантиссе после запятой. А целая часть — всегда 0.

Фиксированная и плавающая точка: разница

Кажется, будто мантисса и порядок числа с плавающей запятой — это что-то сложное. А вычисления с дробями можно проводить проще. Например, считать целую и дробную часть разными сущностями. Такой формат действительно существует и называется числом с фиксированной точкой. Вот как он устроен:

• На целую и на дробную часть выделяется фиксированное количество бит. Например, 6 бит для целой и 4 бита для дробной частей.
• И целая, и дробная часть представлены как двоичные числа, которые в процессе вычислений можно преобразовать в десятичные.
• Если какая-то часть начинает занимать больше места, чем выделенные на нее биты — может произойти переполнение и искажение результатов.

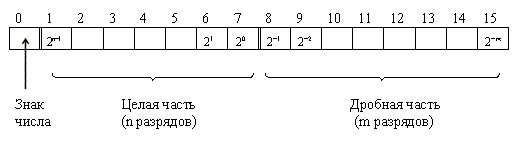
С одной стороны, это удобно — числа в таком формате конечные. С ними не получится бесконечных дробей, компьютеру проще проводить операции, и вычисления работают быстрее. С другой стороны, у таких чисел есть погрешность, связанная с особенностями хранения.

Погрешность в числах с фиксированной точкой зависит от того, сколько бит выделили на целую и дробную часть. 

Для примера возьмем двоичную запись двух чисел с фиксированной точкой: 001,111 и 001,110. Они различаются на одно двоичное 000,001. Интуитивно кажется, что и в десятичном виде разница между ними будет равна 0,001. Но фактически выходит не так:

• 001,111 = 1,875
• 001,110 = 1,75

Настоящая разница — 0,125. Это то, чему равна та самая двоичная 000,001, если после запятой выделено 3 бита. А еще это шаг, минимальная разница между соседними числами, которые можно записать в таком формате. Шаг окажется другим, если увеличить количество бит, выделенных на одно число, — но он будет существовать всегда.

Из-за этой особенности числа с фиксированной точкой используют там, где производительность важнее точности. То есть вычисления нужно проводить быстро, а погрешность не так страшна. А если нужна точность — используют вычисления с плавающей запятой.

Особенности чисел с плавающей точкой

У формата данных с плавающей точкой есть несколько особенностей. Их нужно знать, чтобы при работе с ними не возникало вопроса, почему получился тот или иной результат. 

Хранение особых чисел

Ноль. Первая особенность формата — отсутствие нуля в привычном понимании. Вместо него есть два нуля: положительный и отрицательный float 0. Мантисса и экспонента таких чисел заполнены нулями, а вот знаковый бит может меняться в зависимости от того, положительный это ноль или отрицательный.

Бесконечность. То же самое происходит с другим особым числом — бесконечностью. Их в float тоже две: положительная и отрицательная. Записываются они как числа, где экспонента заполнена единицами, а мантисса — нулями.

Неопределенность. В стандарте IEEE 754 ее обозначают выражением NaN — Not a Number. Обычно его можно встретить, если попытаться записать в числовую переменную нечисловое значение, например букву. Но это может быть и математическая неопределенность вроде результата деления бесконечности на бесконечность. Экспонента такого числа заполнена единицами, а в мантиссе есть хотя бы одна единица.

Нормализация чисел

Числа с плавающей точкой бывают нормализованными и денормализованными. Нормализованные используют для работы с относительно большими значениями. А денормализованные — для значений, которые очень близки к нулю.

• Нормализованные числа ближе к научной записи письма. В них коэффициент может быть от 1 до 9, а мантиссой считается дробная его часть. Например, 1,2 × 10³. Такие числа занимают в памяти меньше места, а первый бит мантиссы в их двоичной записи всегда равен 1.
• Денормализованные числа — такие, где коэффициент всегда меньше 1. Например, 0,2 × 10³. Мантисса такого числа начинается с 0. Они занимают больше места, но с ними ниже риск, что какое-то очень маленькое число округлится и превратится в 0.

Обычно считается, что денормализованные числа начинаются с числа 0,75. Все, что выше, считается нормализованным. 

С денормализованными числами сложнее работать. Вычисления с ними менее стабильны, а некоторые программы вообще могут приводить их к нулю. Но иногда, при работе с очень маленькими величинами, без них не обойтись. Например, в научных вычислениях.

Точность

С этой особенностью все проще, чем с нормализацией. Дело в том, что, кроме обычного типа float, есть еще и расширенный. В нем на одно число отводится больше бит, поэтому оно может быть более точным и состоять из большего количества цифр. Это и есть точность.

• Числа одинарной точности содержат 32 бита. Это стандартный тип float в большинстве языков программирования. Один бит в них — знаковый, 23 бита выделено на мантиссу, а еще 8 — на экспоненту. Этого хватает, чтобы хранить числа с точностью до семи знаков после запятой.
• Числа двойной точности содержат 64 бита. Во многих языках программирования они обозначаются как double. Кроме одного знакового бита, они выделяют 52 бита на мантиссу и 11 на экспоненту. В них можно хранить числа с 15 знаками после запятой.

Диапазон чисел в обоих случаях очень большой. Например, максимальный множитель для чисел типа float — 10 в 38 степени. А для чисел типа double — 10 в 308 степени. Это числа, состоящие из 38 и 308 цифр соответственно.

Как работать с числами с плавающей точкой

В большинстве языков программирования существуют свои типы данных для чисел с фиксированной и плавающей точкой. В случае с плавающей точкой это может быть float или double, хотя в ряде языков типы могут называться иначе. Достаточно создать переменную нужного типа, задать ей значение — и можно проводить операции с дробями. Есть и отдельные функции для разных действий:

• деление дробных чисел;
• округление вверх или вниз;
• отбрасывание дробной части;
• перевод в целое число и так далее.

В программировании мантиссу и экспоненту не нужно постоянно держать в голове. Компьютер вычисляет все сам. Современные языки позволяют работать с дробными числами в привычном человеку формате.

И все-таки понимать, как дроби в программировании устроены внутри, необходимо. Это поможет понять, в чем дело, если где-то возникнет ошибка, или при необходимости оптимизировать операции с плавающей точкой.

Коротко о числах с плавающей точкой

• Числа с плавающей точкой — один из способов хранения дробей в памяти компьютера. Кроме них, существуют еще и числа с фиксированной точкой, менее точные, но более быстрые для вычислений.
• В памяти числа с плавающей точкой хранятся как комбинация из знакового бита, мантиссы и экспоненты. Мантисса содержит значимые цифры числа, а экспонента — множитель для мантиссы. Ее умножают на экспоненту, чтобы получить нужное число.
• В программировании числа с плавающей точкой обычно хранятся в переменных типа float. Или double, если нужен расширенный тип: там на одно число выделяется не 32, а 64 бита.
• У чисел с плавающей точкой два нуля и две бесконечности: положительные и отрицательные. Это бывает важно при работе с очень маленькими значениями и с точными вычислениями.