Деревья решений: как устроены и для чего их используют в анализе данных

Метод дерева решений помогает разбить задачу на последовательные этапы, где на каждом шаге принимается промежуточное решение, приближая к финальному ответу. Такие деревья похожи на настоящие: у них также есть корни (начальные точки) и ветки, ведущие к листьям (конечным результатам). 

В статье разбираемся, как устроены деревья решений, как их построить и где полезно использовать.

Из чего состоит дерево решений

Структура дерева решений начинается с корневого узла, который по ветвям ведет к ряду внутренних узлов и листьев. 

• Корневой узел (root node) — начальная точка. В ней задается основной вопрос, ставится первая задача, от которой ветви пойдут к следующим.
• Узел, или внутренний узел (internal node) — задает следующий вопрос или ставит условие. От ответа зависит, по какой ветке следовать дальше. 
• Ветвь (branch) — это путь, ведущий к следующему узлу или листу.
• Лист (leaf) — конечный результат, «ответ» на поставленный в начале вопрос, где дерево решений заканчивается.

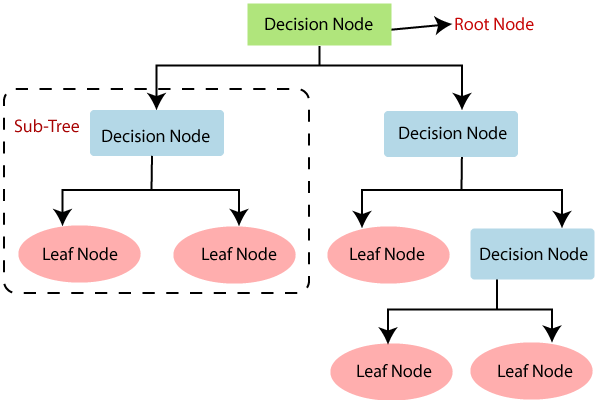
Как это работает: дерево решений последовательно задает вопросы, переходя на разные ветки, пока не дойдет до финального «листа», где выдаст конечный результат.

К одному листу могут вести несколько ветвей. Это означает, что разные пути (последовательности условий) иногда приводят к одному и тому же ответу.

Простой пример: нужно определить, что за фрукт лежит на столе — яблоко или груша.

Условия:

1. если цвет зеленый и форма округлая, то это яблоко;
2. если цвет желтый и форма округлая, то это яблоко;
3. если цвет желтый и форма овальная, то это груша;
4. если цвет зеленый и форма овальная, то это груша.

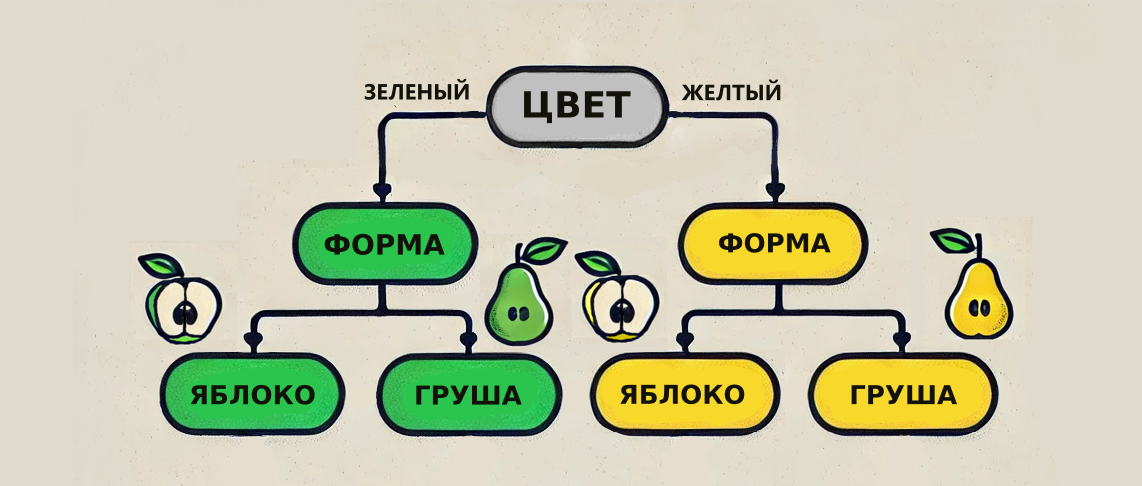
Дерево решений:

• Цвет = Зеленый
  
  Форма = Округлая → Яблоко
  
  Форма = Овальная → Груша

• Цвет = Желтый
  
  Форма = Округлая → Яблоко
  
  Форма = Овальная → Груша

Какие есть способы построения деревьев решений 

Существует два основных подхода: ручной и с помощью алгоритмов машинного обучения. 

Построение дерева вручную

При ручном построении можно использовать следующие инструменты.

Электронные таблицы — полезны для анализа данных, визуализации и ручного построения дерева. Основные варианты:

• Microsoft Excel — подходит для построения небольших деревьев решений. В нем удобно работать с ограниченными датасетами. Для автоматизации можно установить специальные надстройки, например XLMiner, которые упрощают создание дерева решений. 
• Google Таблицы — также можно использовать для построения простых деревьев решений. Подходят для базового анализа и работы с небольшими объемами данных, особенно в командах, где требуется совместное редактирование. 

Среды для рисования и создания схем — платформы для создания диаграмм и визуализации — позволяют рисовать детализированные деревья без ограничений. Вот несколько примеров:

• Lucidchart — простой в использовании инструмент для создания диаграмм, включая деревья решений. Можно легко перетаскивать элементы, добавлять условия и связи.
• Microsoft Power BI — платформа для анализа данных и создания деревьев решений. Подходит для интерактивных отчетов и работы с большими данными.
• Decision Tree Maker от Visual Paradigm — специализированная программа для деревьев решений. Позволяет легко строить и редактировать диаграммы с узлами и ветвями.

Построение дерева с помощью моделей машинного обучения

Дерево решений можно создать с помощью алгоритмов ML. Для этого сначала загружаются данные, и модель обучается выявлять взаимосвязи между признаками и результатами. После такого обучения алгоритм строит дерево, где каждый узел — это условие, а каждый лист — ответ.

Модель можно внедрять в веб- и мобильные приложения и системы управления данными. Когда алгоритм получит входные данные, он предскажет результат. С помощью метрик, полученных при оценке модели, можно анализировать ее эффективность и принимать решения о дальнейшей оптимизации.

Популярные инструменты для создания таких деревьев

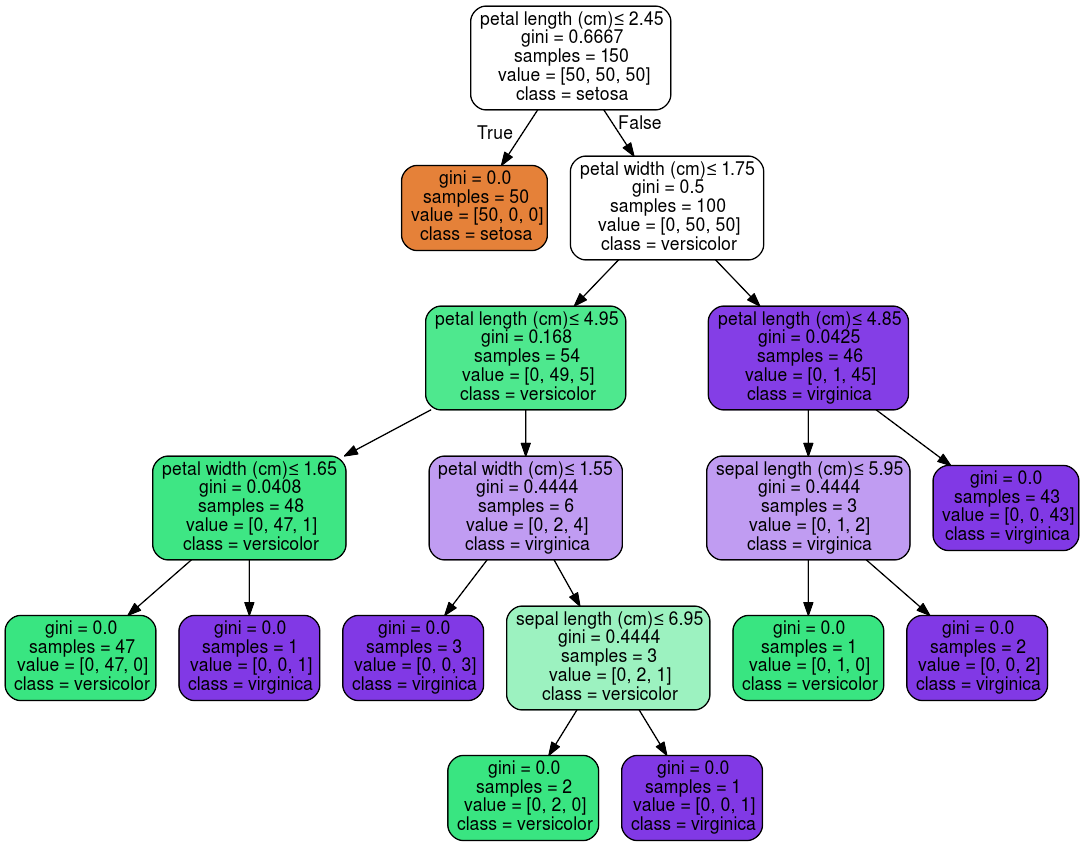
Scikit-learn — библиотека Python для задач классификации и регрессии, где можно настраивать параметры модели.

Как использовать:

• Импортировать библиотеку и загрузить данные.
• Выбрать алгоритм (например, DecisionTreeClassifier или DecisionTreeRegressor).
• Обучить модель на обучающем множестве, протестировать ее на отложенных данных.

XGBoost — это реализация алгоритма градиентного бустинга, который строит ансамбль из деревьев решений для повышения точности модели. Работает на Python и R.

Как использовать:

• Установить библиотеку.
• Создать модель XGBoost, обучить ее на тренировочном датасете и протестировать.

rpart — пакет для анализа и прогнозирования для R, который упрощает создание деревьев решений.

Как использовать:

• Загрузить пакет rpart.
• Построить дерево, которое можно использовать для прогнозов.

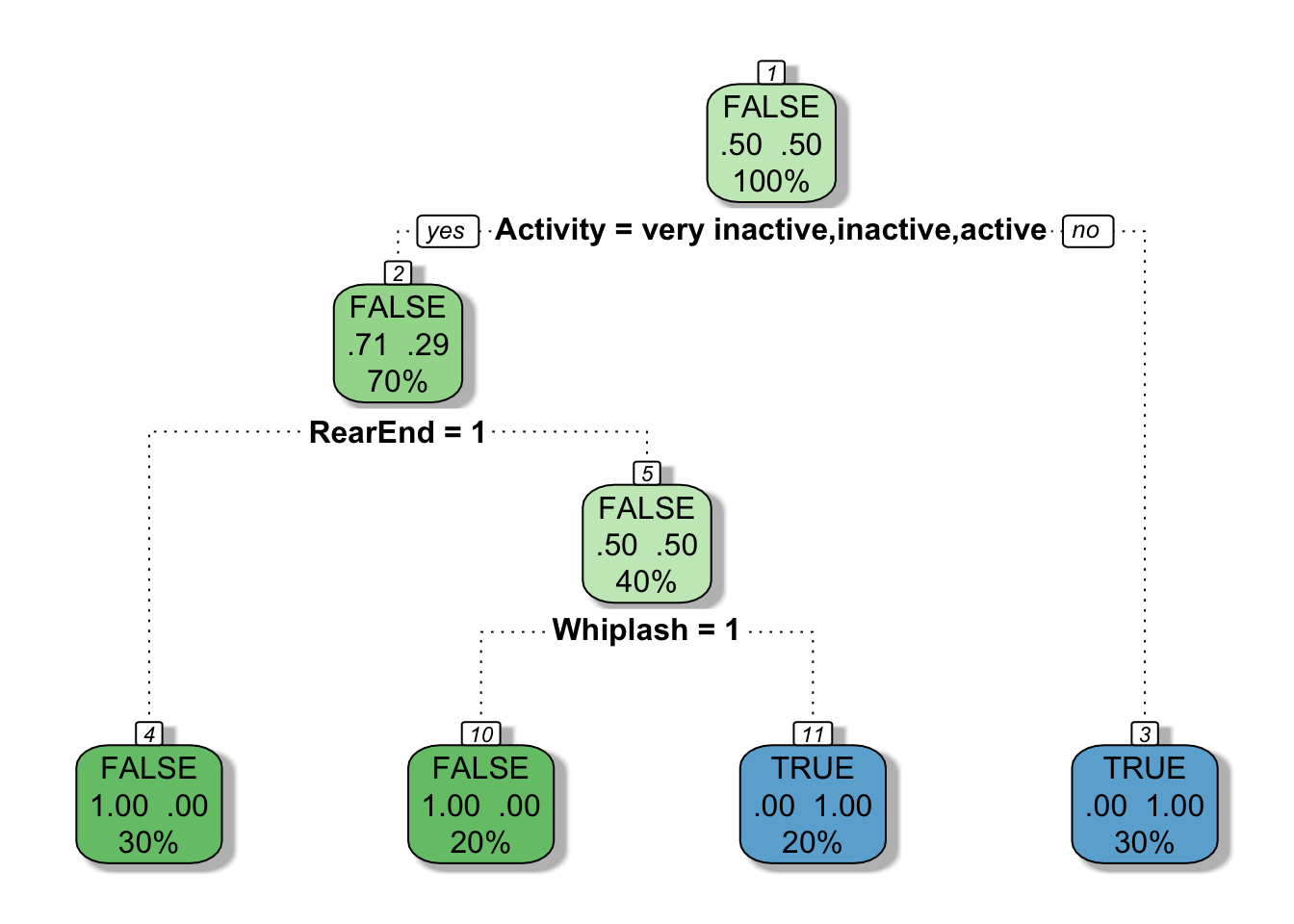
C5.0 — библиотека для построения деревьев, основанная на алгоритме Куинлана. Обычно используется в языке R.

Как использовать:

• Импортировать библиотеку.
• Обучить модель на данных, затем проанализировать результаты и, при необходимости, настроить параметры для повышения точности.

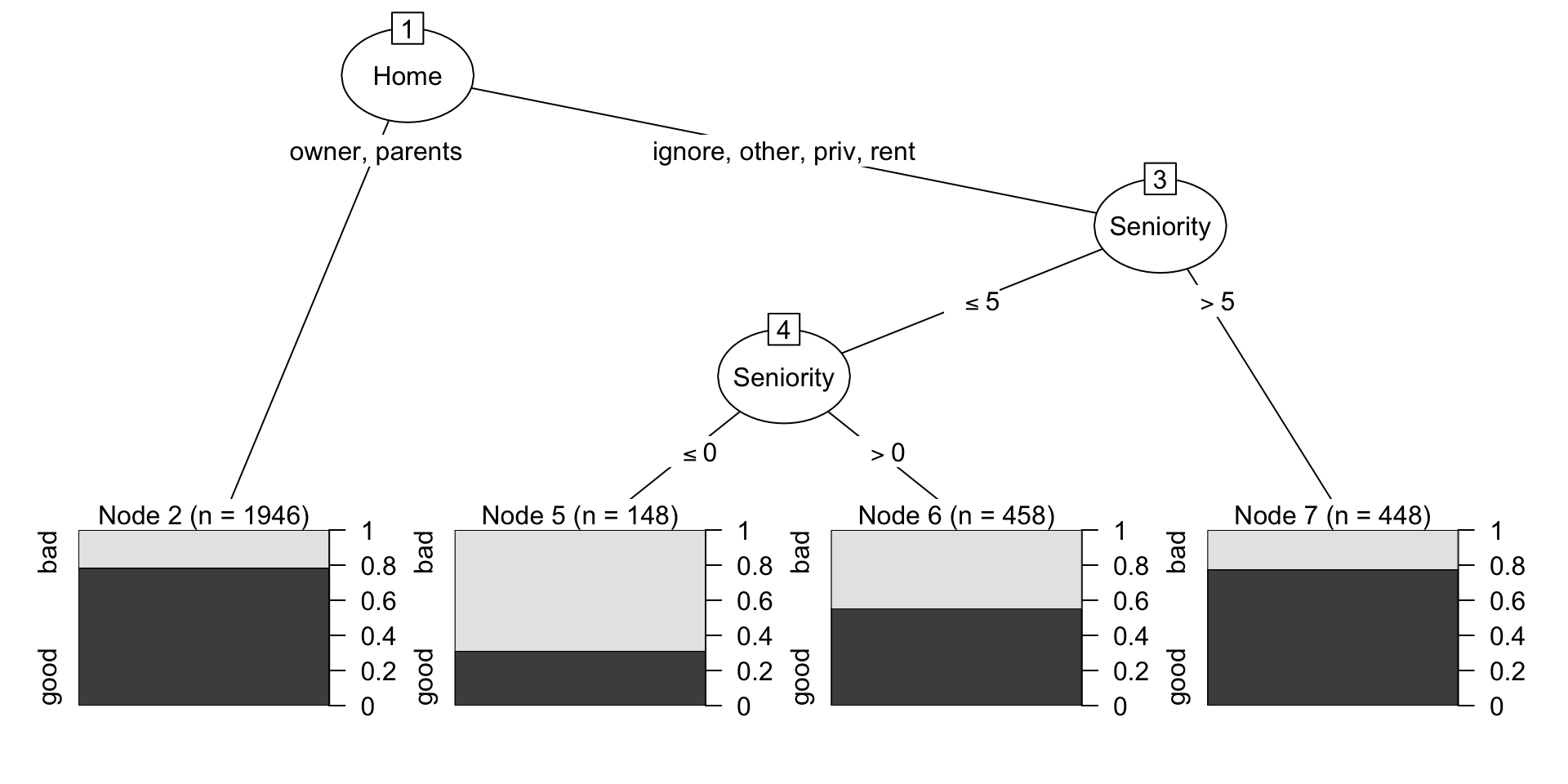
Как выглядит процесс построения дерева решений

Этап 1 — Определение цели и сбор данных

Цель — нужно четко сформулировать задачу, которую нужно решить, например оценить вероятность определенного события.

Сбор данных — подобрать качественные данные, подходящие для анализа. Это могут быть файлы, базы данных, датасеты или потоки данных, которые содержат признаки, влияющие на конечное решение.

Пример: допустим, цель — предсказать, купит ли покупатель продукт. Данные будут включать демографические, психологические и поведенческие характеристики покупателей.

Этап 2 — Выбор признаков и разбиение данных

На этом этапе нужно выявить наиболее важные признаки для разбиения данных. Это разделение датасета на подмножества на основе выбранного атрибута (признака).

На каждом узле выбираем критерий, который наилучшим образом разделяет данные на однородные группы. 

Пример:

Шаг 1 — корневой узел (возраст)

Начинаем с признака «Возраст», который лучше всего делит покупателей на группы:

• молодые (до 30 лет): 80% не покупают, 20% покупают;
• взрослые (30 лет и старше): 40% не покупают, 60% покупают.

Шаг 2 — узел 1 (молодые покупатели)

Следующий признак — «Доход». Разделим молодых покупателей на две группы:

• низкий доход: 90% не покупают, 10% покупают;
• высокий доход: 50% не покупают, 50% покупают.

Шаг 3 — узел 2 (взрослые покупатели)

Для взрослых покупателей используем признак «Место проживания»:

• проживание в городе: 30% не покупают, 70% покупают;
• проживание в пригороде: 60% не покупают, 40% покупают.

Процесс разбиения продолжается до выполнения условий остановки, таких как минимальный размер узла или достижение заданной глубины дерева.

Критерии разбиения данных

Рассмотрим, как именно оценивать правильность выбора признака для разбиения данных. Для этого есть следующие критерии.

Энтропия (неопределенность). Показывает, насколько группы данных являются определенными и однородными после разбиения. Чем ниже энтропия, тем лучше разбиение.

$$
H(S) = — \sum_{i=1}^{c} p_i(P_i)
$$

где:

• H(S) — энтропия множества S;
• c — количество классов в данных;
• p_i — вероятность того, что случайно выбранный объект принадлежит классу i.

Индекс Джини — это еще один показатель однородности групп данных. Чем ниже индекс Джини, тем больше данных относится к одной категории. Поэтому выбирают такие условия, чтобы индекс был минимальным.

$$
G(S) = 1 — \sum_{i=1}^{c} p_{i}^{2}
$$

где:

• G(S) — индекс Джини для множества S;
• c — количество классов в данных;
• p_i — вероятность того, что случайно выбранный объект принадлежит классу i.

Алгоритмы построения дерева

Существуют алгоритмы построения деревьев решений, которые используют разные подходы для разбиения данных. Рассмотрим основные из них.

ID3 (Iterative Dichotomiser 3)

Выбирает признак, который максимально уменьшает энтропию. Для этого он использует информационную выгоду, которая показывает, насколько хорошо признак делит данные на группы.

Применение: подходит для небольших наборов данных и задач классификации, но плохо работает с непрерывными (числовыми) признаками и склонен к переобучению.

C4.5

Это улучшение алгоритма ID3. Он может обрабатывать как категориальные, так и числовые признаки. Алгоритм использует нормализованную информационную выгоду для выбора признаков.

Применение: эффективен на сложных наборах данных с непрерывными признаками.

CART (Classification and Regression Trees)

Использует либо классификацию (для категориальных данных), либо регрессию (для числовых данных). Для этого алгоритм применяет индекс Джини для оценки «чистоты» разбиений.

Применение: это универсальный алгоритм, который подходит для классификации и регрессии и широко используется в анализе данных и машинном обучении.

Этап 3 — Условия остановки

При построении дерева решений важно определить условия, при которых процесс остановится. Это необходимо для предотвращения переобучения и создания слишком сложной модели. 

Дерево строится до тех пор, пока не выполнится одно из условий остановки:

1. Достигнута определенная глубина дерева
   
   Максимальная глубина дерева — это максимально допустимое количество уровней, которое может иметь дерево. 
   
   Например, если она установлена на уровне 5, дерево не будет расти дальше этого, даже если данные все еще могут быть разделены.

2. Количество данных в узле становится слишком маленьким
   
   Если количество объектов в узле падает ниже заранее заданного порога, то дальнейшее деление может быть нецелесообразным.

3. Не удается улучшить разделение данных
   
   Когда разбиение данных не приводит к улучшению (например, не уменьшает энтропию или индекс Джини), алгоритм может остановиться.

Этап 4 — Отсечение ветвей

В процессе построения дерева решений может получиться так, что модель стала слишком сложной и переобученной. Чтобы улучшить модель и сделать ее более устойчивой к новым данным, применяют отсечение ветвей (pruning). Существует два вида.

Предварительное отсечение (Pre-Pruning

С его помощью можно ограничить рост дерева до того, как оно станет слишком сложным. Основные методы:

• Максимальная глубина. Устанавливают ограничения на максимальную глубину дерева.
• Минимум единиц данных на лист. Устанавливают минимальное количество единиц данных в каждом листе.
• Минимум единиц данных для разбиения. Указывают минимальное число единиц данных для деления.
• Максимальное количество признаков. Вводят ограничение на максимальное число признаков для разбиения.

Последующее отсечение (Post-Pruning)

Это удаление узлов или ветвей после завершения роста дерева. Основные методы:

• Отсечение для сокращения стоимости и сложности. Этот метод позволяет отсечь неэффективные ветви и повысить эффективность модели. 
• Отсечение излишних ветвей. Удаление ветвей, которые не влияют на общую точность.

Этап 5 — Оценка и тестирование дерева

После построения дерево тестируют на новых данных, чтобы убедиться, что оно правильно классифицирует или предсказывает результаты.

Применение метода на практике

Рассмотрим, как работает дерево решений, на примере задачи.

Задача

Банку нужен алгоритм, по которому он будет определять, одобрять клиенту кредит или нет. Критериями будут такие факторы, как возраст, доход, кредитная история и статус занятости. 

На основании данных о предыдущих клиентах можно будет построить дерево решений для определения платежеспособности следующих клиентов.

Этапы построения упрощенного дерева решений

1. Сбор данных
   Собираем данные о клиентах, включающие следующие параметры:

• Возраст: до 25 лет, 25–40 лет, более 40 лет.
• Доход: низкий, средний, высокий.
• Кредитная история: положительная или отрицательная.
• Статус занятости: трудоустроен или нет.

2. Построение дерева решений

• Корневой узел. Начинаем с выбора критерия с наибольшей информационной выгодой. В данном случае это может быть кредитная история.
  

• Первый уровень разбиения
  
  Если кредитная история положительная, идем по ветке к узлу «Высокая вероятность одобрения».
  
  Если кредитная история отрицательная, идем по ветке к узлу, где проверяются другие факторы.

3. Дальнейшее разбиение узлов

• Узел 1: если кредитная история положительная, проверяем доход.
  
  Лист 1: если доход высокий, итоговое решение — одобрено.
  
  Лист 2: если доход средний, также итог — одобрено (с некоторыми оговорками).
  
  Лист 3: если доход низкий, итог — отказано.

• Узел 2: если кредитная история отрицательная, проверяем возраст.
  
  Лист 4: если возраст старше 40 лет и доход высокий, итог — одобрено.
  
  Лист 5: если возраст старше 40 лет и доход низкий, итог — отказано.
  
  Лист 6: если возраст младше 25 лет, независимо от дохода, итог — отказано.
  
  Лист 7: если возраст от 25 до 40 лет и доход высокий, итог — одобрено.
  
  Лист 8: если возраст от 25 до 40 лет и доход низкий, итог — отказано.

Так выглядит примерная структура дерева решений, хотя в реальных ситуациях она гораздо сложнее и подробнее.

Итоги

• Деревья решений — это метод, который помогает принять решение и систематизировать данные.
• Дерево состоит из корневого узла (root node), внутренних узлов (internal node), ветвей (branch) и листьев (leaf).
• В корневом узле задают начальный вопрос. Затем по веткам ответов последовательно переходят к следующим узлам или листьям. Узлы «задают» вопрос, а листья выдают результат.
• К одному результату (листу) могут приводить несколько ветвей.
• Деревья решений можно строить вручную с помощью электронных таблиц и платформ для визуализации. Также деревья создают с помощью моделей машинного обучения.
• Чтобы создавать обученные модели деревьев решений, нужно разбираться в машинном обучении и знать языки программирования. У Python и R есть специальные библиотеки для построения деревьев решений.
• Процесс построения дерева решений состоит из нескольких этапов. В него входят определение цели, сбор данных, выбор признаков, разбиение данных, остановка построения, отсечение ветвей и тестирование дерева.