Градиентный спуск: что это такое и почему его так любят в ML

Градиентный спуск — это один из первых алгоритмов, который изучают начинающие дата-сайентисты. Это популярный метод обучения моделей машинного обучения. Его улучшенные версии используют как в нейросетях, так и в классических ML-моделях.

Разбираемся, как работает градиентный спуск, вместе с экспертом Марией Жаровой, Data Scientist в компании Wildberries.

Что такое градиентный спуск

Градиентный спуск — алгоритм оптимизации, который помогает найти минимум функции. Он работает с градиентом, или вектором первых частных производных — показывает направление, в котором функция растет быстрее всего. Также существует антиградиент: направление, в котором функция быстрее всего убывает.

Сейчас разберем, как это происходит.

Допустим, у нас есть функция f(a, b), где a и b — это коэффициенты, которые нужно подобрать так, чтобы значение функции было минимальным. Чтобы найти подходящие коэффициенты, применяется градиентный спуск. 

Вот как это выглядит:

1. Сначала вычисляют градиент функции f(a, b) — вектор первых частных производных. Этот вектор указывает направление и скорость изменения функции.
2. Затем градиент умножают на заданный размер шага и вычитают из предыдущего значения коэффициента с последнего шага.
3. Затем вычисляют значение функции с новым коэффициентом. Если оно уменьшилось — значит, процесс движется в правильном направлении.
4. Алгоритм продолжают, пока не пройдет достаточное количество итераций или изменения функции не перестанут быть значимыми.

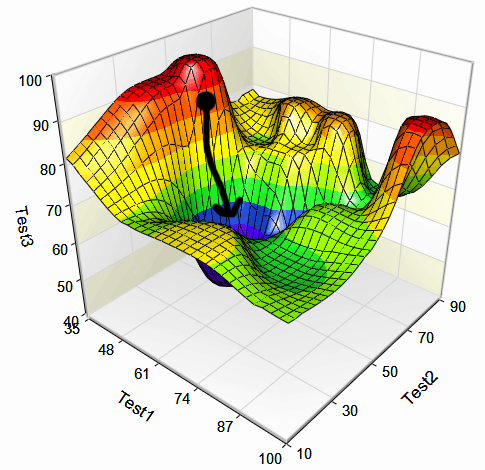
Как используют градиентный спуск в машинном обучении

ML-модели не дают точных результатов, у их предсказаний есть определенная погрешность. Ее называют функцией ошибки, или функцией потерь. Задача специалиста — обучить модель так, чтобы погрешность была минимальной, то есть достичь минимума функции ошибки. 

Для этого в машинном обучении используют градиентный спуск. Градиенты функции потерь помогают найти параметры, или веса модели, которые уменьшают ошибку предсказаний на обучающей выборке. 

Фактически с помощью градиентного спуска ищут точку, где график ошибки будет минимальным. Параметры этой точки и есть оптимальные коэффициенты для модели.

Градиентный спуск применяется в современных ИИ-моделях, включая нейросети и классические алгоритмы машинного обучения. Чаще всего используют усовершенствованные версии алгоритма, которые ускоряют вычисления или повышают их точность. Например:

• стохастический градиентный спуск — при расчете весов использует только один из обучающих примеров в выборке;
• мини-батч — в каждой итерации выбирает случайно сформированное небольшое количество обучающих примеров;
• добавление моментума, или импульса — вместо расчета новых градиентов использует среднее по прошлым градиентам, чтобы стабилизировать и ускорить обучение.

Пример градиентного спуска для функции ошибки

Как и любой стандартный метод оптимизации, градиентный спуск — итеративный алгоритм. Он повторяет определенные шаги, пока не достигнет нужного результата, и обновляет веса по формуле. 

Алгоритм для поиска минимальной ошибки можно описать так:

1. Выбрать функцию ошибки между истинными значениями, или таргетом, и предсказаниями модели. В простейшем случае подойдет среднеквадратичная ошибка.
2. Задать начальные значения параметров модели w_0. Рекомендуется задавать случайные начальные значения параметров, а не устанавливать их в ноль, чтобы избежать симметрии при обучении.
3. Найти градиент функции — вектор частных производных — по весам модели \nabla L(w_0).
4. Обновить веса по формуле w_{k+1} = w_k — \alpha * \nabla L(w_k), где \alpha — шаг алгоритма, или learning rate.
5. Повторять шаги 3-4 или заданное количество раз, или до момента, пока ошибка не перестанет значительно меняться.

Что учесть при работе с градиентным спуском

Метод приобрел популярность благодаря сочетанию скорости и точности. Он позволяет обучать модели быстро и снижать погрешности, особенно при использовании улучшенных версий. Также градиентный спуск подходит для работы с функциями ошибок, у которых много параметров.

Но при работе с ним стоит помнить о трех моментах:

1. Ошибку алгоритма нужно отслеживать на каждой его итерации. Удобнее всего визуализировать ее на графике.
2. Шаг градиентного спуска, или learning rate, влияет на качество модели. Результаты обучения могут различаться при одном и том же количестве итераций, но с разными шагами. Поэтому рекомендуется сравнивать несколько графиков для разных значений learning rate и подбирать оптимальный размер шага.
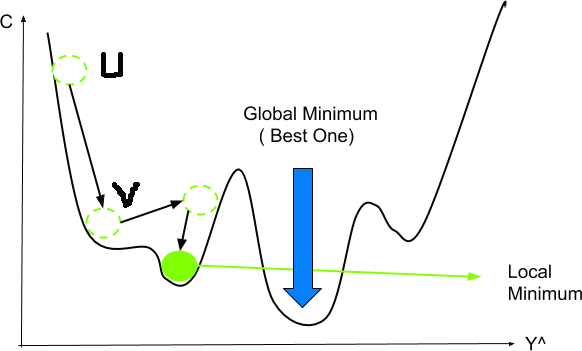
3. Рекомендуется использовать улучшенные версии алгоритма, а не стандартный. Классический градиентный спуск может допустить ошибку — найти не глобальный, а локальный минимум функции, то есть минимальное значение на каком-то небольшом участке.

Работать с алгоритмом можно с помощью языков программирования, которые применяются в ML, например Python. Как правило, метод уже реализован в большинстве фреймворков для машинного обучения, таких как TensorFlow или PyTorch. Поэтому считать вручную ничего не нужно — процесс обычно автоматизирован.

Какие проблемы могут возникнуть при использовании метода

У градиентного спуска есть свои слабые места. При работе с ним может возникнуть несколько распространенных проблем, но в современном ML для них уже придумали решение. Разберем их подробнее.

Переобучение. Так называется ситуация, когда модель оказывается слишком хорошо натренирована на обучающих примерах, а на реальных дает неточные результаты. Чтобы избежать такого эффекта, используют l1 или l2-регуляризацию — добавляют «штраф» за слишком сложные параметры модели, которые указывают на переобучение.

Взрыв градиентов. Это явление, когда градиент начинает неконтролируемо и неограниченно расти и выходит за допустимые значения. Со взрывами помогает справиться все та же регуляризация или клиппинг (ограничение градиента по модулю).

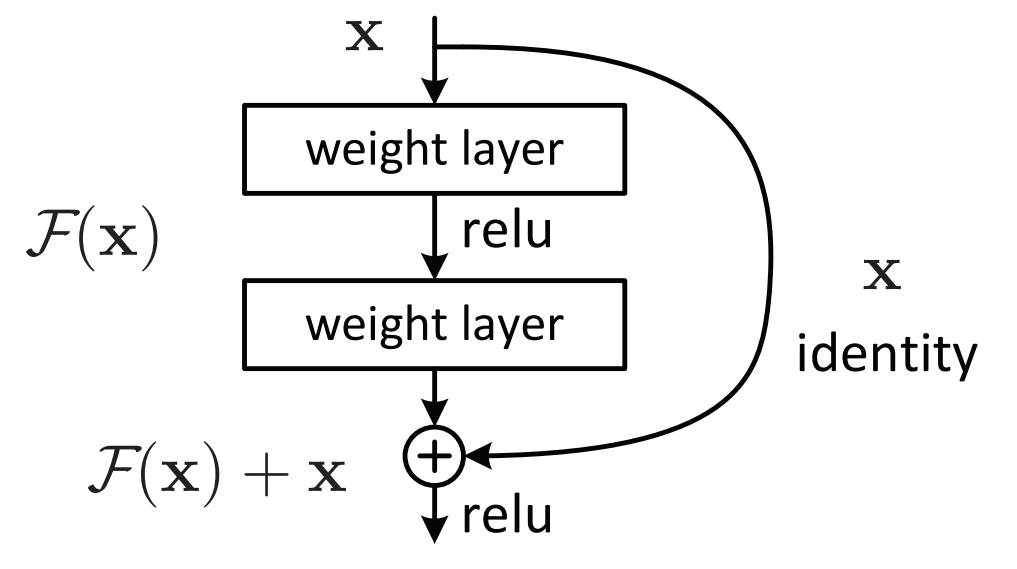
Затухающий градиент. Его еще называют исчезающим. В этом случае значения, наоборот, становятся близкими к нулю и продолжают уменьшаться по мере прохождения слоев модели. В результате скорость обучения падает, а нужных результатов иногда не получается достичь. Для устранения проблемы используют специальные архитектурные решения, например глубокое остаточное обучение, где вход нейросети напрямую соединяется с выходом.

Есть ли у градиентного спуска альтернативы?

Существует еще несколько методов оптимизации. Они тоже помогают находить минимум функции, но используются в ML крайне редко. Например:

• Метод Ньютона — метод оптимизации второго порядка, в котором используют вторые производные. Для работы с ним понадобится рассчитывать гессиан функции потерь — он описывает поведение функции по втором порядке. Это более затратно с точки зрения вычислений. Хотя метод позволяет быстрее достичь нужной точки, он требует больших мощностей и тоже может «застревать» в локальных минимумах функции.
• Методы нулевого порядка — в них вообще не используются градиенты. За основу берут физические и биологические процессы. Например, метод отжига имитирует броуновское движение. Такие способы подходят не для всех задач, а их точность и скорость сложнее оценить.
• Алгебраические методы — например, решение линейной регрессии через метод наименьших квадратов. Они используются в относительно простых задачах, но не подходят для обучения сложных нейронных сетей.

По сравнению с ними градиентный спуск более сбалансирован и предсказуем, поэтому его и используют намного чаще. Хотя знать об альтернативных подходах всё равно стоит: они могут пригодиться в некоторых случаях. Например, в задачах поиска оптимального маршрута или в ситуациях, когда градиент функции вычислить невозможно.

Что почитать и посмотреть о градиентном спуске

На тему машинного обучения существует множество материалов. Мы отобрали несколько, которые пригодятся начинающему дата-сайентисту и помогут разобраться подробнее в том, как устроен градиентный спуск. Вот с какими источниками стоит ознакомиться:

• И. Гудфеллоу, Й. Бенжио, А. Курвилль. «Глубокое обучение». Градиентному спуску посвящена отдельная глава, но книга в целом дает хорошее представление о работе с моделями.
• StatQuest. YouTube-канал на английском языке, где наглядно разбираются различные понятия из машинного обучения, в том числе градиентный спуск. 
• fmin.xyz. Сайт преподавателя МФТИ, где он разъясняет понятия из теоретической математики и оптимизации. Ресурс включает текстовые статьи, ссылки на видеолекции преподавателя и практические материалы. Подойдет для продвинутого изучения теории.

Краткие выводы

• Градиентный спуск — один из основных методов обучения моделей в ML. Его применяют как для нейросетей, так и для других типов моделей из-за точности и скорости обучения.
• В основе метода — поиск минимума функции. С помощью производных от функции ошибки он помогает найти значения, при которых ошибка становится близкой к минимуму.
• На практике чаще всего применяют улучшенные версии алгоритма: стохастический, с мини-батчем или добавлением моментума.
• У градиентного спуска есть свои слабые места: он может находить локальный минимум, а не глобальный, а градиент способен затухать или «взрываться». Для устранения этих ошибок используют специальные модификации.