Разбираемся, что такое система уравнений и как решать системы уравнений с двумя или тремя неизвестными. А еще — рассказываем о решении задач при помощи систем.
Что такое системы уравнений
Допустим, нам нужно решить следующую задачу: длина Днепра и Дона вместе равна 4255 км. Днепр длиннее Дона на 315 км. Какова длина рек по отдельности?
Нам требуется узнать две величины: длину Днепра и длину Дона. Обозначим через x, например, длину Дона. Нужно учесть, что Днепр длиннее Дона на 315 км. Значит, чтобы выразить длину Днепра, надо к длине Дона прибавить 315 км. В задаче имеется еще одно данное — общая длина Днепра и Дона.
Мы можем выразить эту длину, сложив уже выраженные через x длины Дона и Днепра и таким образом длина Дона и Днепра вместе может быть записана как \(x+(x+315)\). Так как общая длина Днепра и Дона по условию задачи равна 4255 км, то составляем следующее уравнение:
Решив уравнение, найдем, что \(x=1970\). То есть длина Дона равна 1970 км. А значит, длина Днепра равна 1970 + 315 = 2285 км.
То, что мы выше решили, — это уравнение с одной переменной. Но в жизни часто надо решать уравнения с несколькими переменными. Приведем простой пример. Допустим, брат старше сестры в два раза, но также известно, что вместе им 30 лет. Сколько брату и сестре лет по отдельности?
Обозначим сумму возрастов брата и сестры как \(x+y = 30\). Тогда, если учитывать, что брат старше сестры в два раза и что возраст сестры обозначен через x, то y мы найдем из уравнения \(y = 2x\). По отдельности эти уравнения имеют бесконечное множество решений. Например, если взять отдельно уравнение суммы возрастов, то исходя из него выходит, что, если брату будет 20 лет, то сестре должно быть 10 лет. Из уравнения \(y=2x\) получается, что, если брату будет 50 лет, то сестре будет 25 лет и так далее. Таких пар значений может быть бесконечное множество. Чтобы получить одно-единственное решение, нужно объединить эти уравнения в систему:
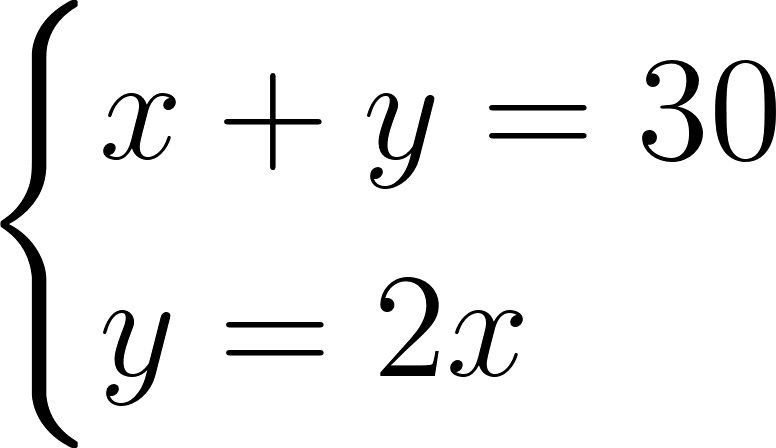
Такие системы называют системами двух уравнений с двумя переменными. Решить систему — это значит найти все пары значений переменных, которые будут превращать в верные равенства оба уравнения системы. Далее рассмотрим самые популярные и универсальные способы решения систем.
Как решать системы уравнений с двумя неизвестными
Метод подстановки
Суть этого метода довольно проста. Нужно из одного уравнения выразить одну переменную через другую, а потом подставить правую часть получившегося выражения во второе уравнение. В системе из предыдущего раздела уже выражена переменная y во втором уравнении. Подставив 2x в первое уравнение, мы получим простейшее уравнение с одной переменной:
Решив его, найдем, что x=10. Подставим x во второе уравнение и найдем, что \(y = 210 = 20\). Таким образом, брату 20 лет, а сестре — 10.
Приведем еще один пример. Решим следующую систему:
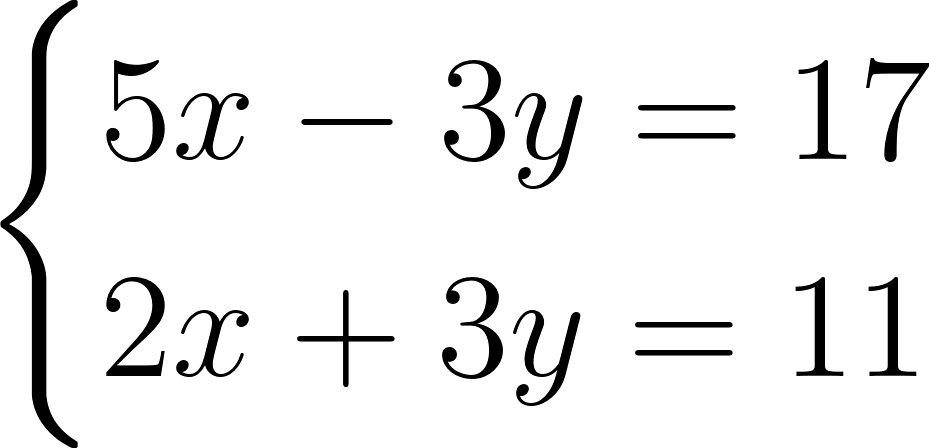
Выразим из второго уравнения одну из переменных, например x, через другую, получим:
Подставим это выражение для x в первое уравнение:
Корнем этого уравнения будет \(y = 1\). Подставив его в выражение для x, найдем:
Таким образом, решением системы являются \(x=4\) и \(y=1\). Далее рассмотрим еще один метод решения систем уравнений.
Метод сложения
Для примера возьмем ту же систему уравнений, которую мы решали способом подстановки в предыдущем разделе:
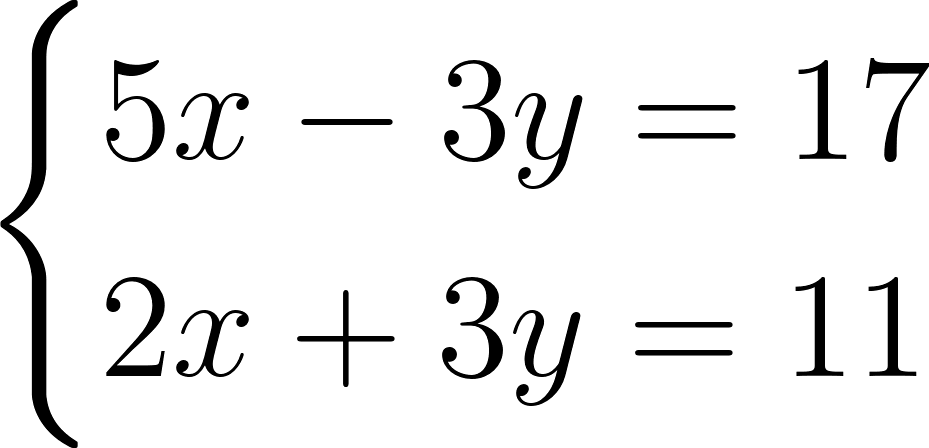
Как видим, коэффициенты при y в обоих уравнениях одинаковы по абсолютной величине и противоположны по знаку. Поэтому если вместо, например, первого уравнения взять сумму данных уравнений, то в этой сумме не будет членов, содержащих неизвестное y. В итоге получим такую систему:
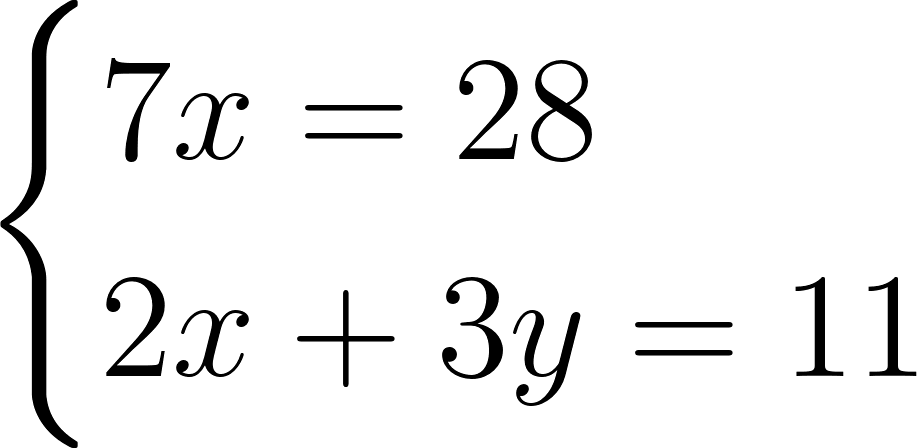
Эта система равносильна исходной, но в ней первое уравнение содержит только одно неизвестное x. Решив это уравнение, найдем, что \(x = 4\). Теперь подставим этот корень во второе уравнение и получим уравнение \(8+3y = 11\), из которого находим \(y = 1\).
Решим еще одну систему:
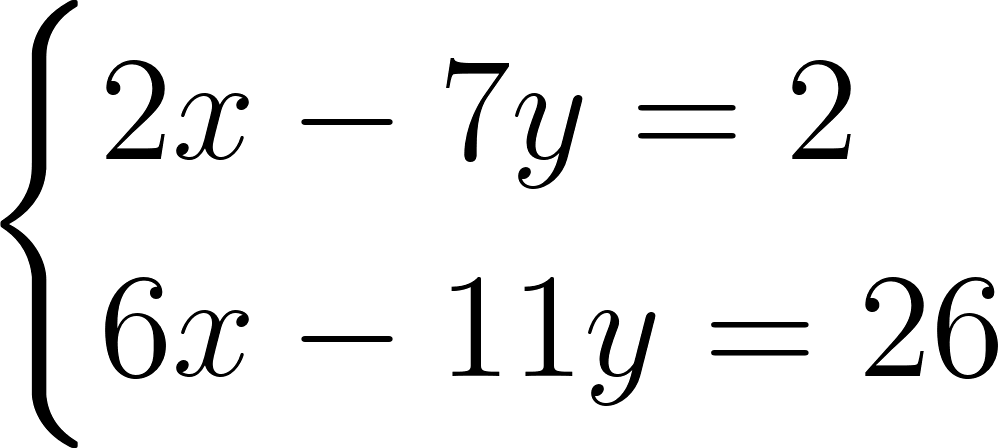
Коэффициенты при x во втором уравнении втрое больше, чем в первом. Умножим обе части первого уравнения на 3. Получим систему, равносильную исходной:
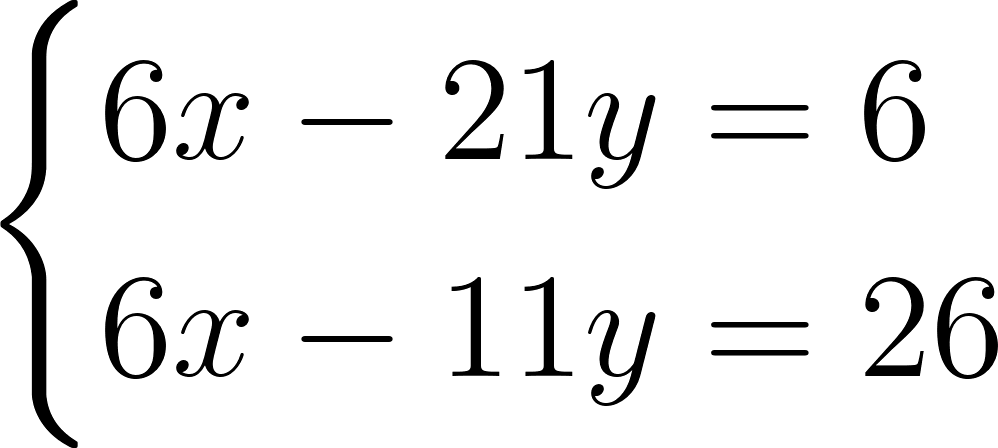
Коэффициенты при x стали одинаковыми. Теперь вычтем второе уравнение из первого. Член, содержащий неизвестное x, пропадет и получится такое уравнение:
Решив его, найдем, что \(y = 2\). Подставив 2 вместо y в одно из исходных уравнений, найдем \(x = 8\). В следующем разделе рассмотрим графический метод решения систем уравнений.
Графическое решение систем уравнений
Пусть дана система уравнений:
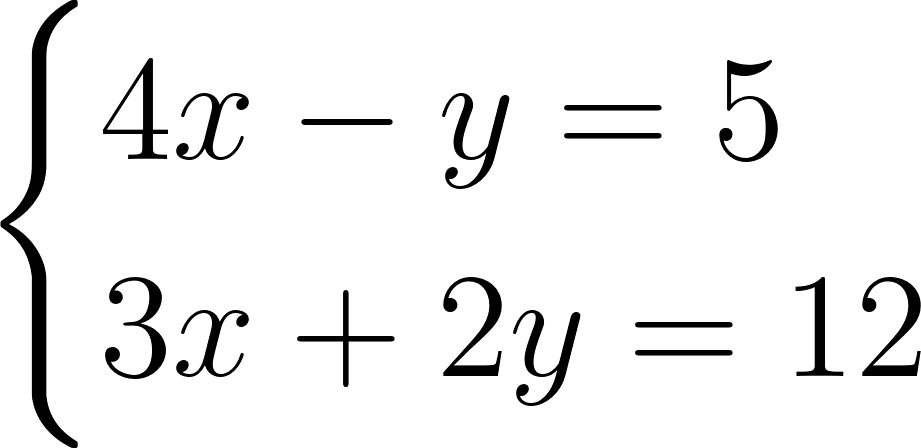
Построим график для каждого уравнения:
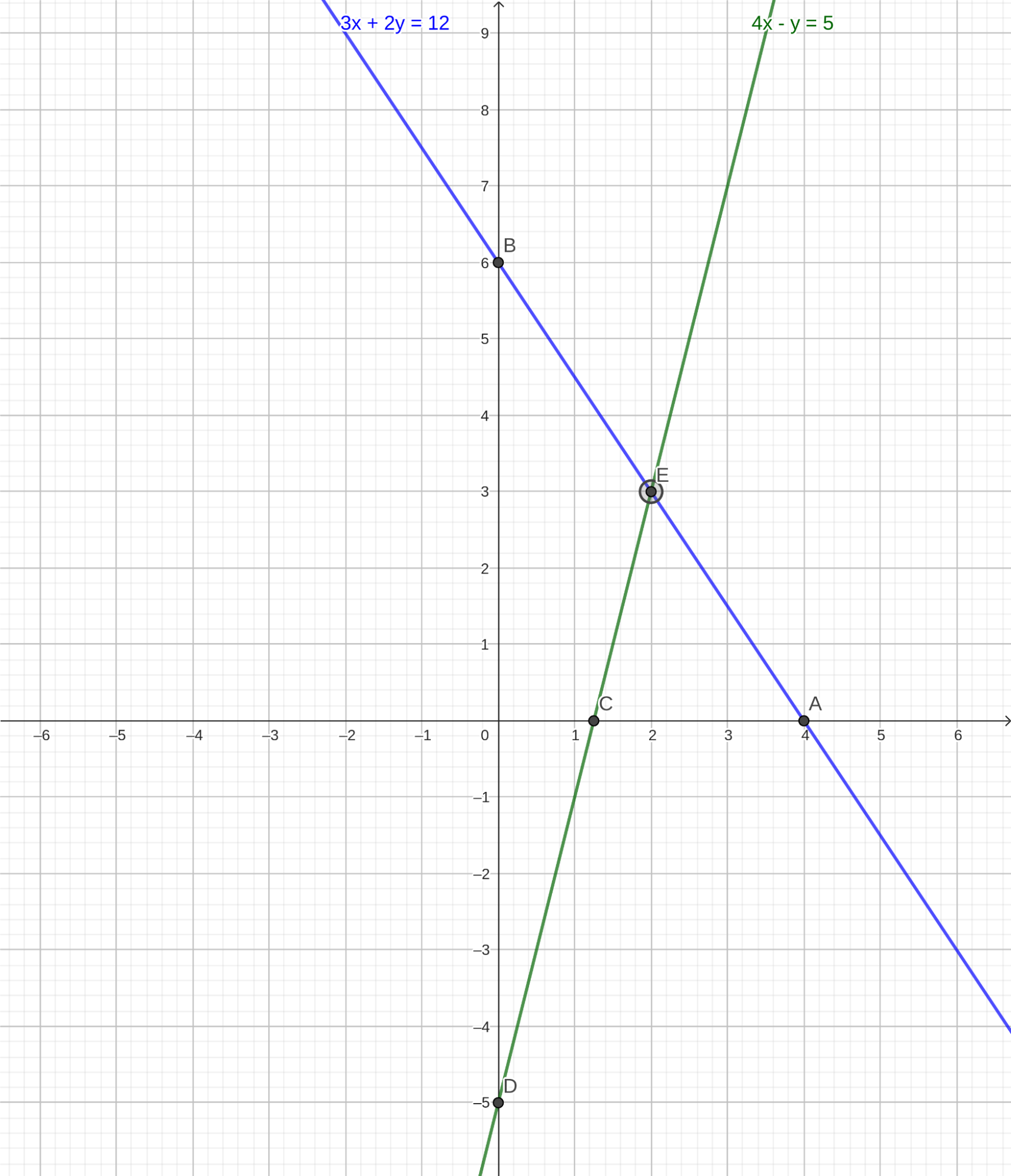
Мы видим две пересекающиеся прямые. Координаты точки E, в которой прямые пересекаются, и есть решение данной системы. Подставим значения координат точки пересечения \(x = 2\) и \(y = 3\) в уравнения системы:
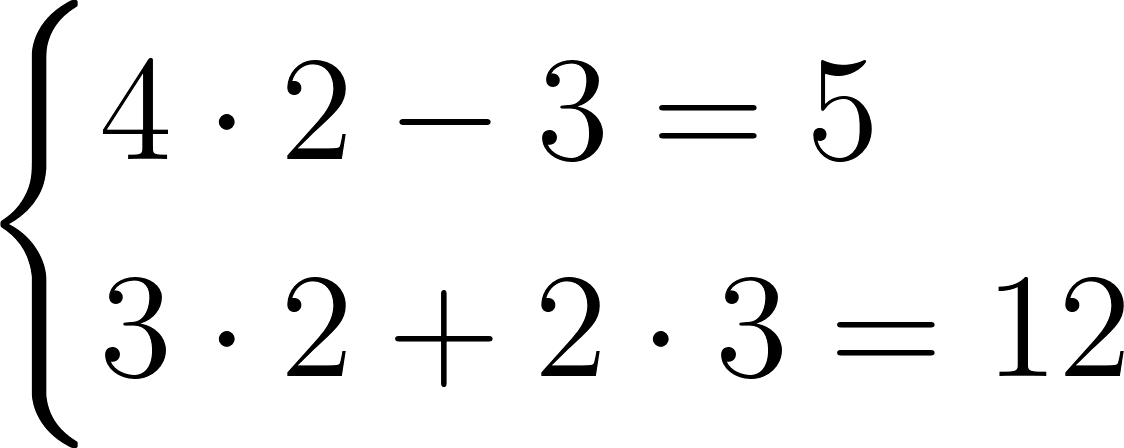
Получилось два верных равенства. Еще один пример:
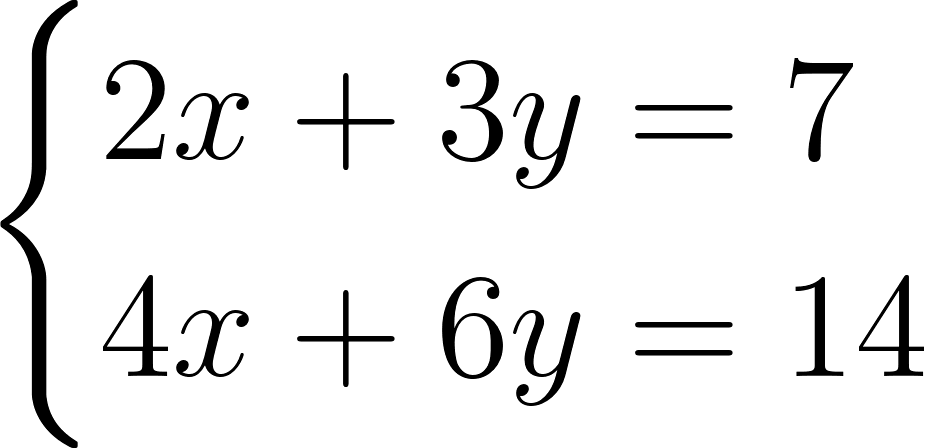
Графиком для этих уравнений будет одна и та же прямая:
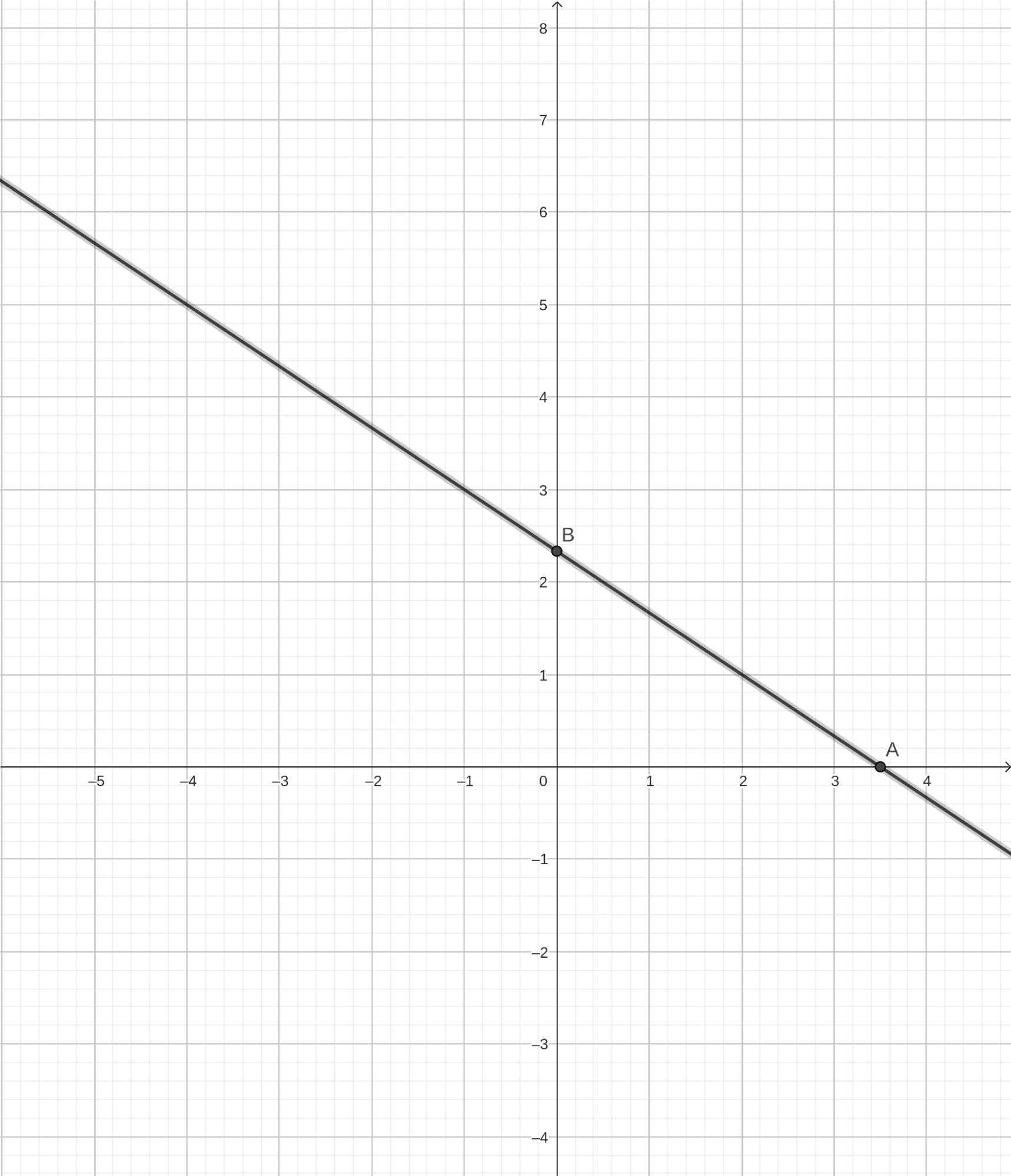
Это значит, что система имеет бесконечное множество решений. Координаты любой точки на этой прямой являются решением системы. Это и понятно. Если разделить обе части второго уравнения на 2, то в результате получим первое уравнение. То есть, уравнения, образующие данную систему, равносильны и всякое решение одного из этих уравнений есть решение другого. Следующий пример:
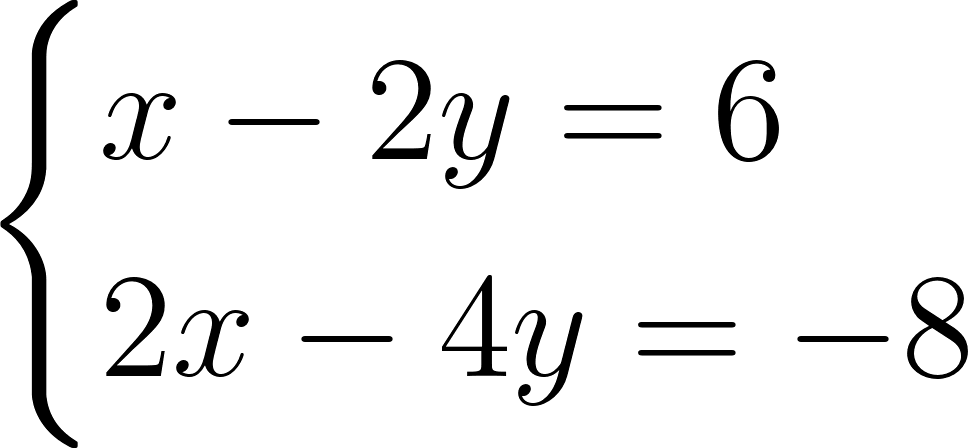
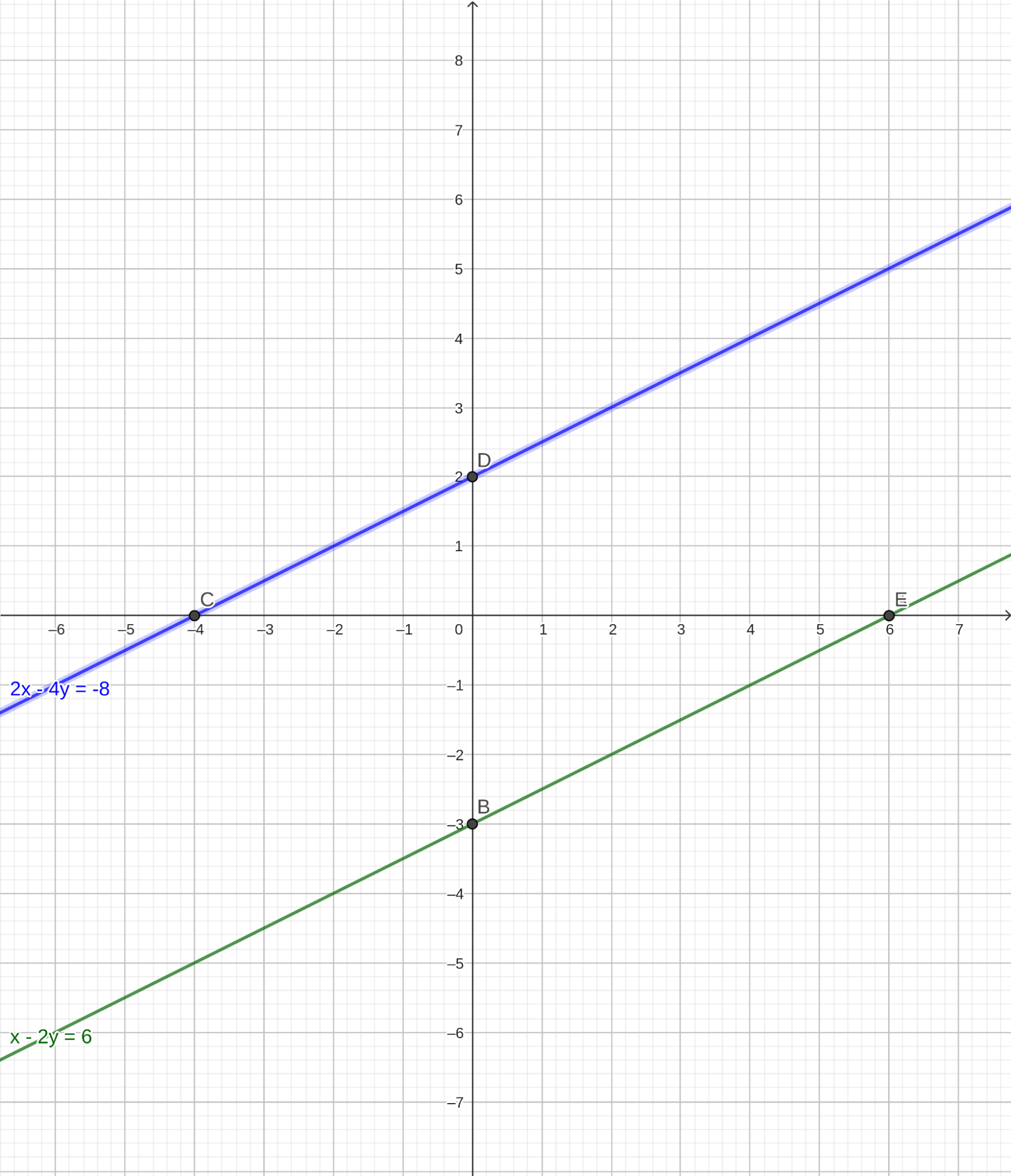
Эти прямые параллельны, а значит, не имеют точек пересечения. Следовательно, и система не имеет решений. В этом можно убедиться и по-другому. Разделив обе части второго уравнения на 2, получим систему, равносильную данной:
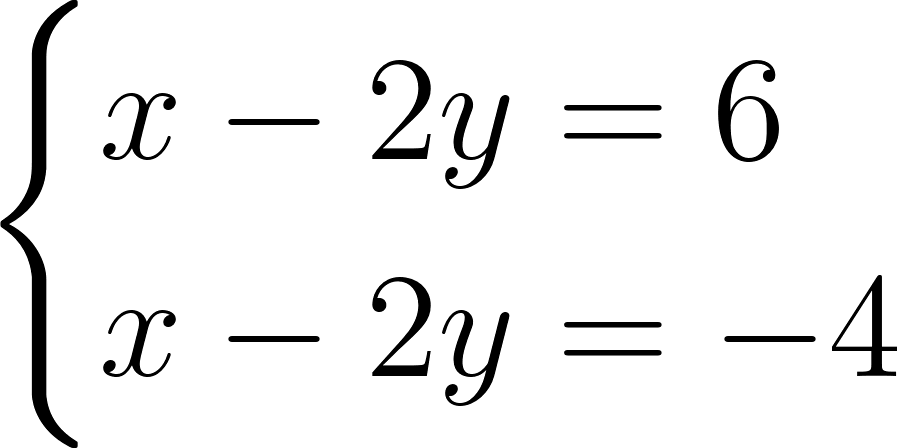
Любая пара значений x и y, подходящая первому уравнению, должна дать для выражения \(x-2y\) значение равное 6 и не может, следовательно, равняться −4, как это следует из второго уравнения.
Как решать системы уравнений с тремя неизвестными
Рассмотрим следующую систему уравнений:
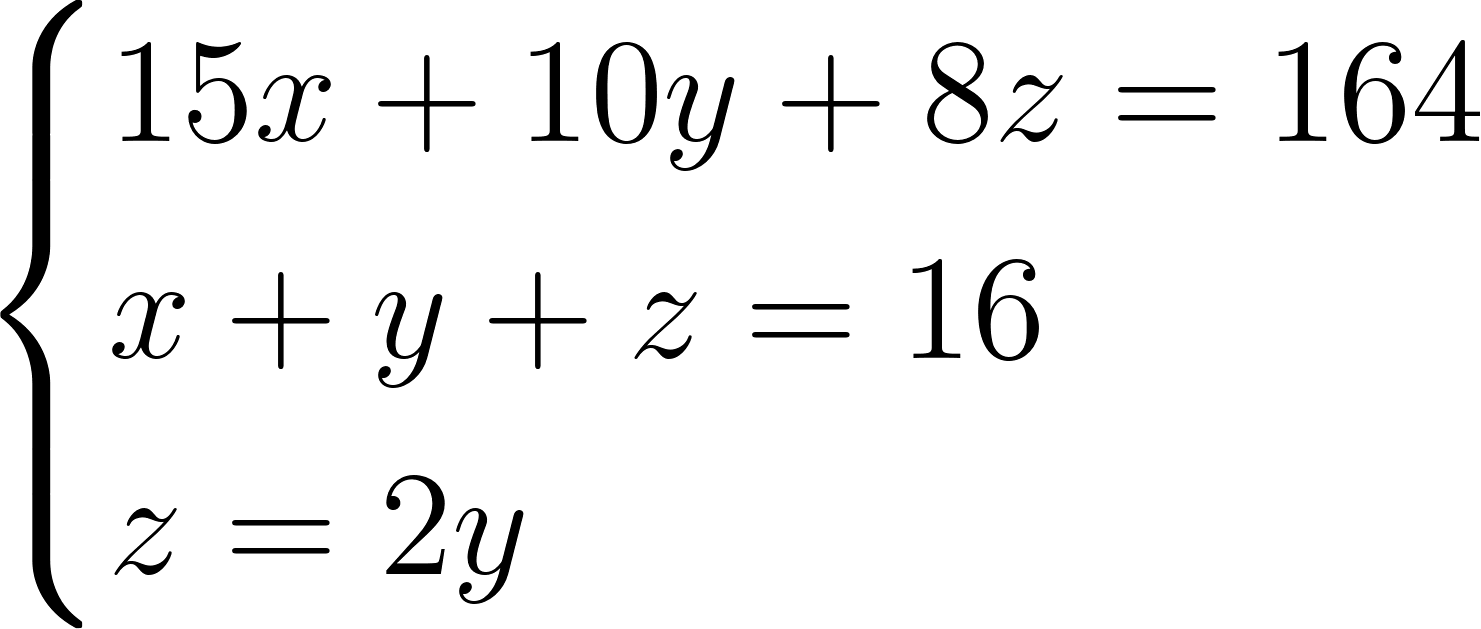
Это система трех уравнений с тремя неизвестными. Попробуем решить ее способом сложения. Так как третье уравнение системы не содержит x, то исключим его из двух остальных уравнений. Для этого умножим обе части второго уравнения на 15. Получим систему:
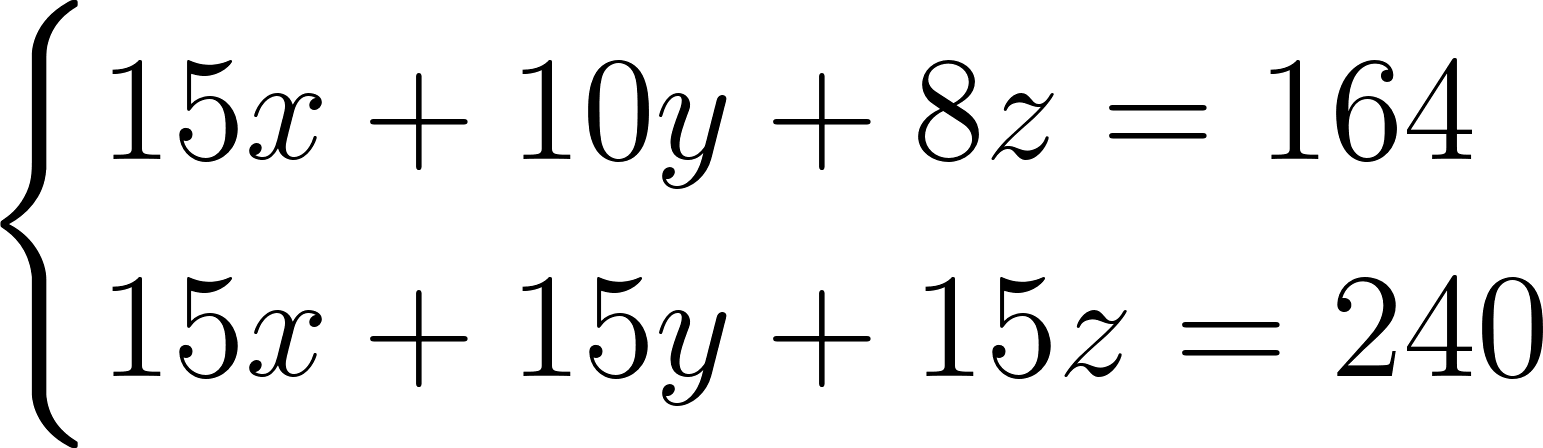
Коэффициенты при x равны. Вычтем из второго уравнения первое и получим \(5y+7z = 76\). Получили уравнение с двумя неизвестными. Вместе с третьим уравнением исходной системы оно образует вот такую простую систему:
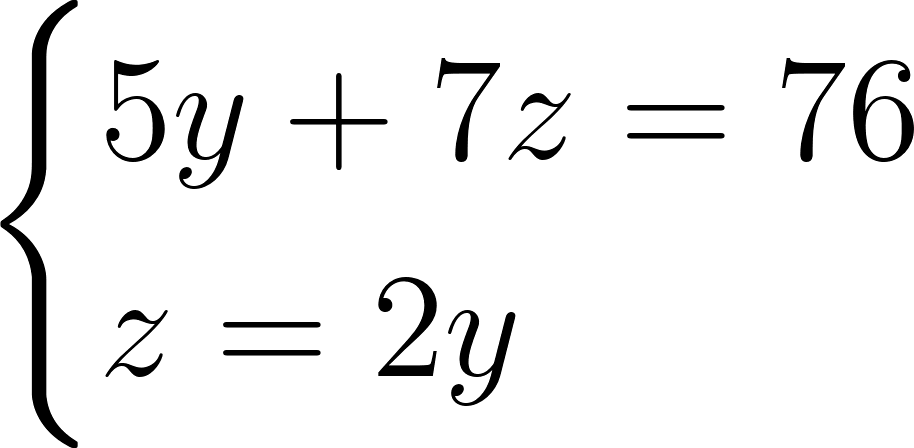
Решив ее, найдем, что \(y = 4\), а \(z = 8\). Подставив эти значения, например, во второе уравнение исходной системы, найдем, что \(x = 4\).
Теперь попробуем решить эту же систему способом подстановки. Этот способ кажется наиболее удобным, так как в третьем уравнении неизвестное z уже выражено через y. Сделав подстановку, получим:
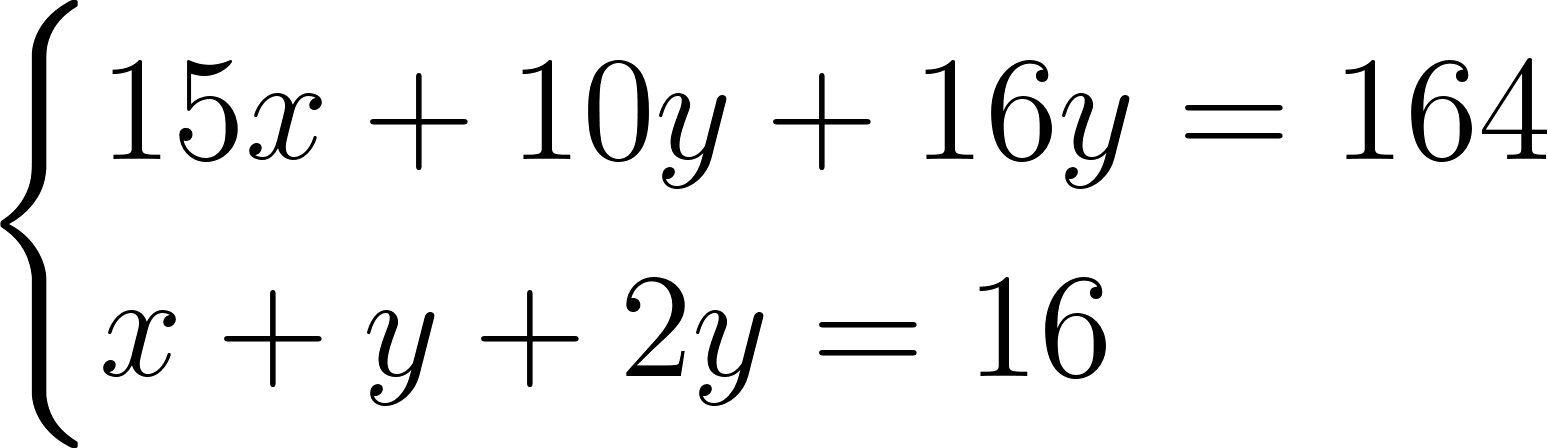
После приведения подобных слагаемых будем иметь:
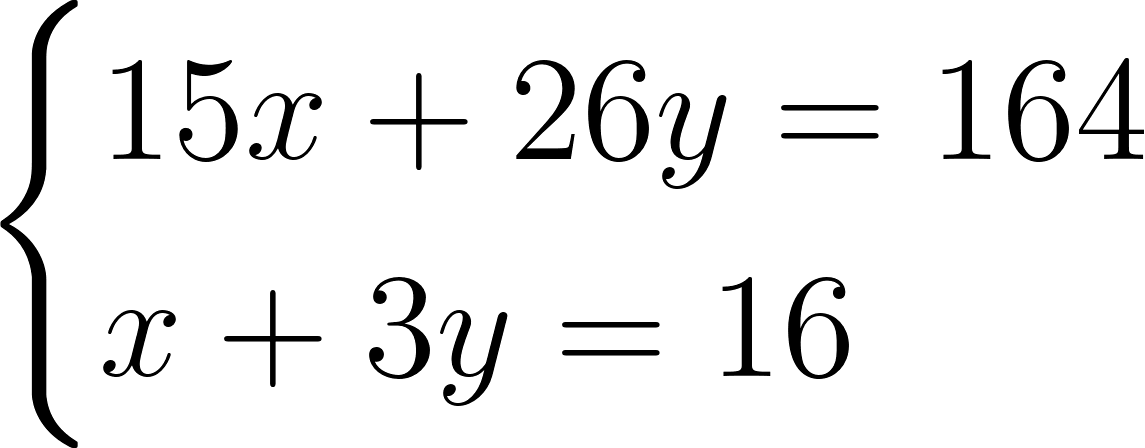
Умножим второе уравнение на 15 и вычтем из него первое уравнение. В результате получим уравнение \(19y = 76\), из которого легко находим, что \(y = 4\). Остальные два корня легко находятся подстановкой.
Решим еще одну систему:
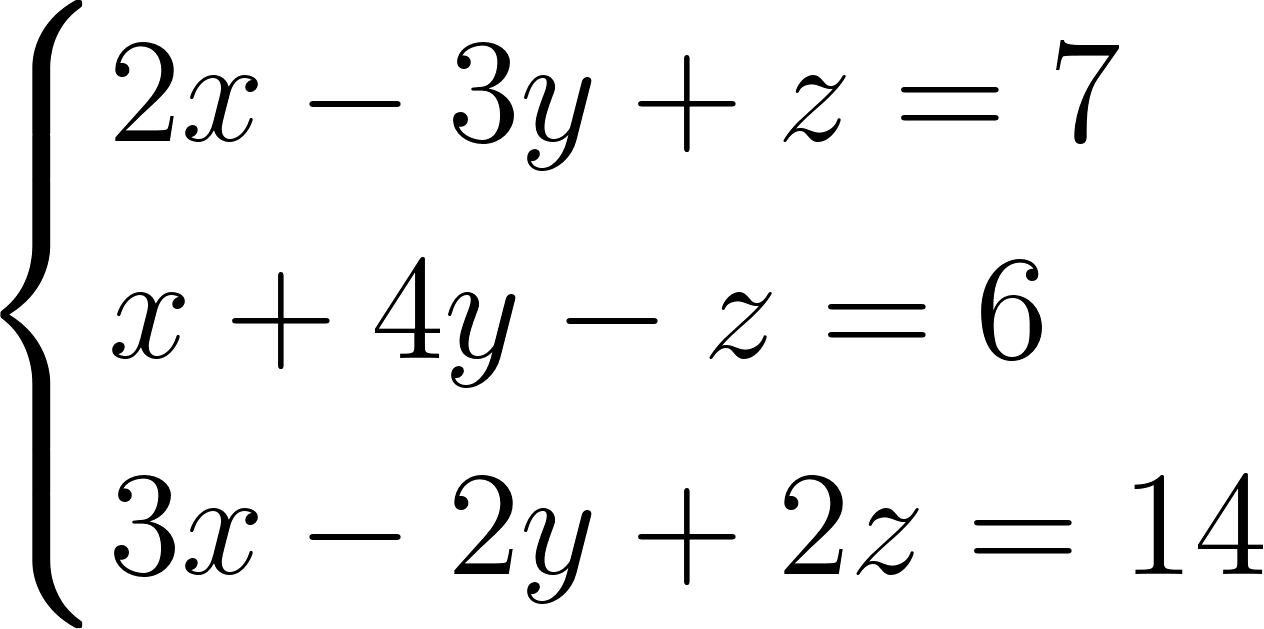
Исключим одно из неизвестных, например z. Для этого сложим первое и второе уравнения. Получим в итоге \(3x+y = 13\). Теперь умножим второе уравнение на 2 и сложим с третьим. В результате у нас получится \(5x+6y = 26\). Эти два уравнения образуют систему уравнений с двумя неизвестными:
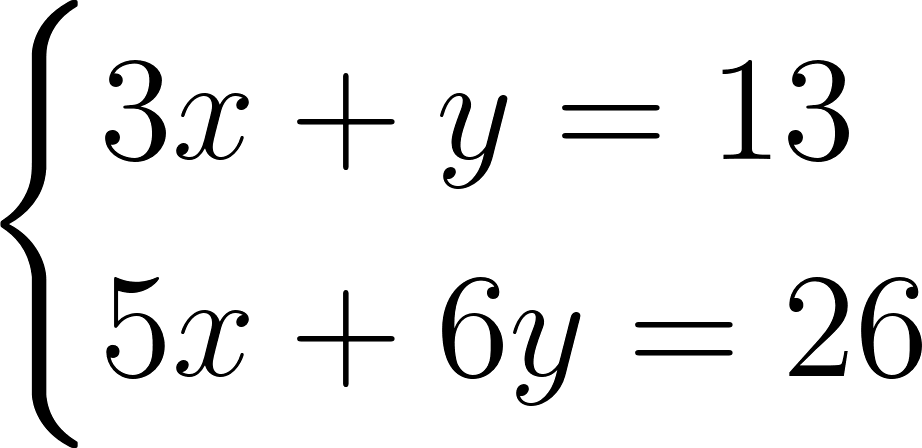
Решив ее, найдем, что \(x = 4\) и \(y = 1\). Далее подставляем эти значения в одно из уравнений исходной системы. Так мы находим, что \(z = 2\). Напоследок рассмотрим еще один пример решения систем уравнений, который иллюстрирует так называемый метод Гаусса. Итак, решим систему:
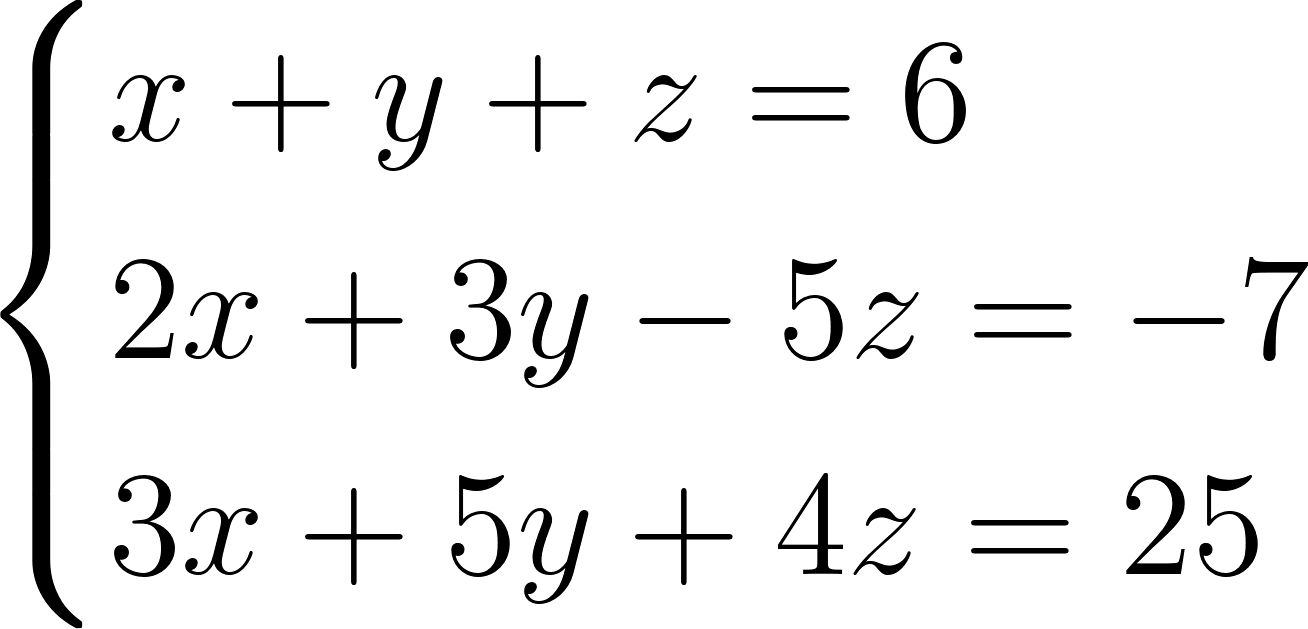
Метод Гаусса предполагает приведение системы к треугольному виду. Для этого неизвестные при помощи элементарных преобразований последовательно исключаются, то есть если в первом уравнении у нас три неизвестных, то во втором их должно быть два, а в последнем — одно. Попробуем проделать такое с указанной выше системой. Прибавим почленно первое уравнение, умноженное на −2, ко второму уравнению и, умноженное на −3, к третьему. Получим систему, равносильную исходной:
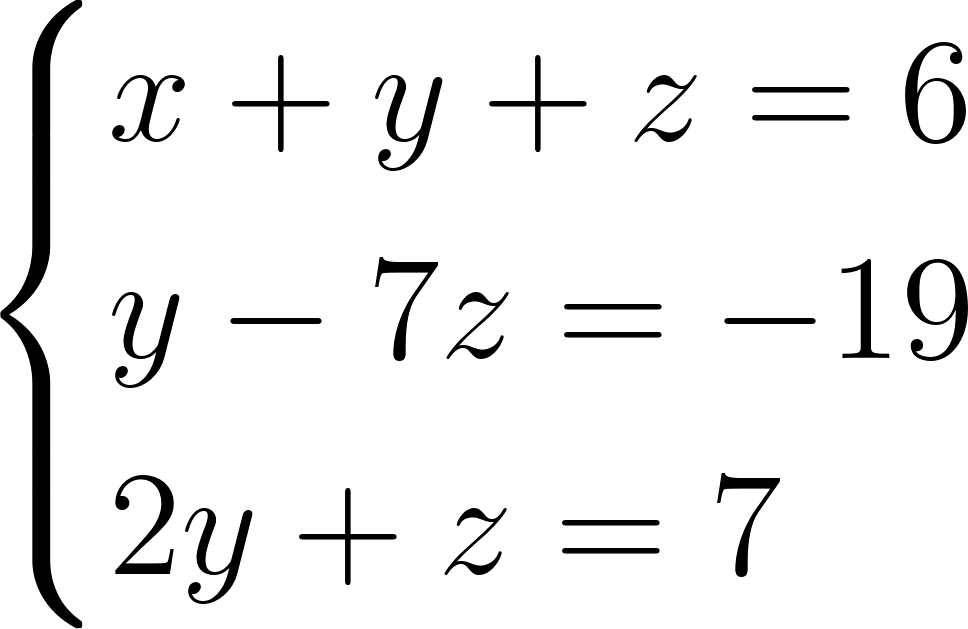
Второе и третье уравнения содержат только y и z. Исключим из третьего уравнения переменную y. Для этого умножим второе уравнение на −2 и прибавим результат к третьему уравнению. Получим:
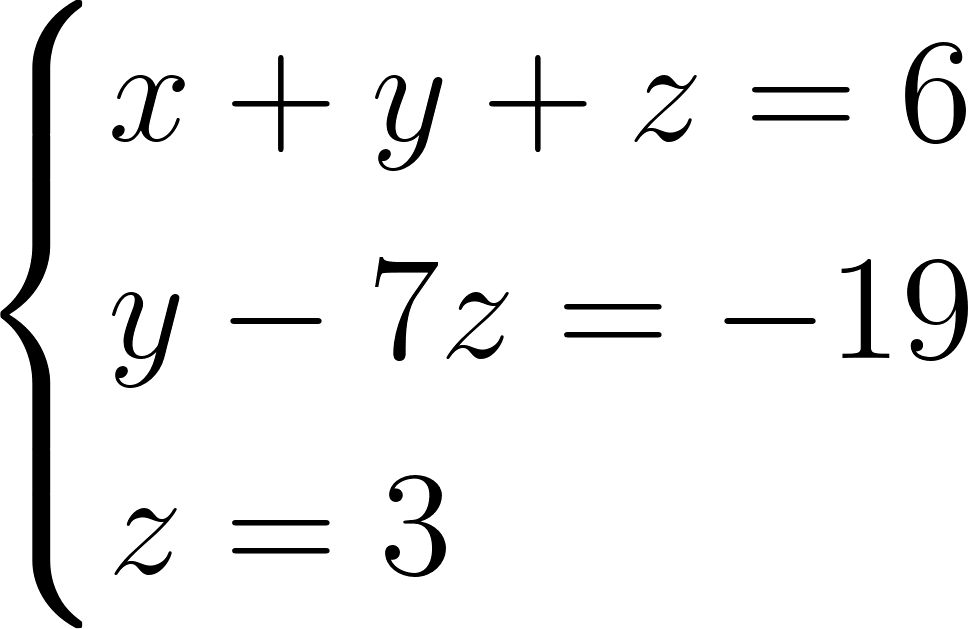
Вот мы и получили систему треугольного вида. Теперь, подставив \(z = 3\) во второе уравнение, находим: \(y = 2\). Далее, подставив \(y = 2\) и \(z = 3\) в первое уравнение, находим: \(x = 1\).
Как решать задачи с помощью систем уравнений
Ранее мы уже решили задачу про возраст сестры и брата при помощи системы уравнений. Покажем еще парочку примеров. Допустим, нам дан прямоугольный треугольник, у которого длины катетов отличаются друг от друга на 23 сантиметра, а длина гипотенузы равна 37 сантиметрам. Найдем катеты этого треугольника.
Обозначим длины искомых катетов через x и y. Тогда разницу катетов можно записать как \(x-y = 23\). Так как нам еще известна длина гипотенузы, то по теореме Пифагора будем иметь следующее выражение:
\(x^2+y^2 = 37^2\) или \(x^2+y^2 = 1369\)
Составляем систему из двух получившихся уравнений:
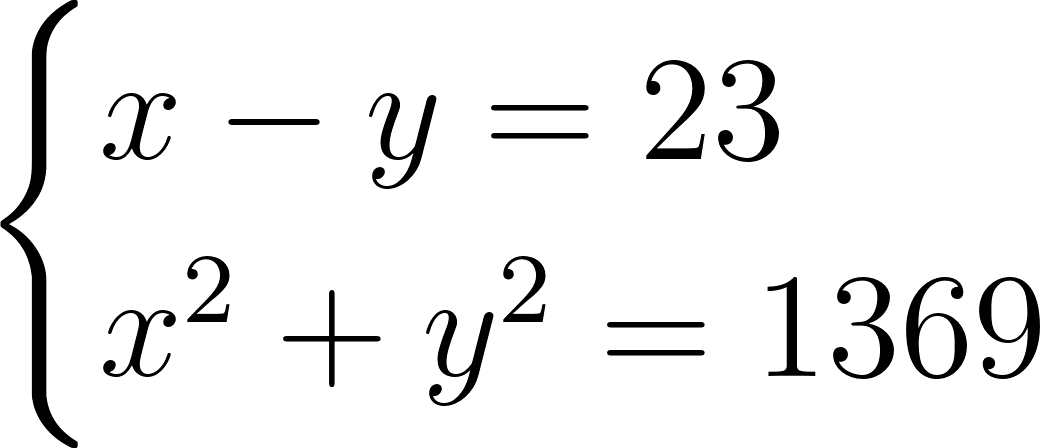
Из первого уравнения выражаем x через y и получившееся выражение подставляем во второе уравнение. Получим:
Проделав все необходимые преобразования, получаем квадратное уравнение \(y^2+23y-420 = 0\), которое имеет два корня \(y_{1} = 12\) и \(y_{2} = -35\). По смыслу задачи подходит только первый корень, так как длина не может выражаться отрицательным числом. Итак, длина одного из катетов равна 12 сантиметрам. Тогда длина другого катета будет \(x = 23+12 = 35\).
Решим еще одну задачу. Расстояние между двумя городами по реке составляет 14 километров. Катер проходит это расстояние по течению за 2 часа, а против течения — за 2 часа и 48 минут. Надо узнать скорость катера в стоячей воде и скорость течения реки.
Для решения этой задачи нам понадобится формула, выражающая путь через скорость и время:
s = vt
Также сразу переведем 2 часа и 48 минут в часы. Это будет \(\frac{14}{5}\) часа. Разберемся с неизвестными. Пусть x км/ч – скорость катера в стоячей воде, а y км/ч — скорость течения реки. Если катер движется по течению, то его скорость будет \(x+y\) км/ч и он пройдет 14 километров за время \(\frac{14}{x+y} = 2\). Если же катер движется против течения, то его скорость \(x-y\) км/ч и он пройдет те же 14 километров за время \(\frac{14}{x-y} = \frac{14}{5}\). Составляем систему:
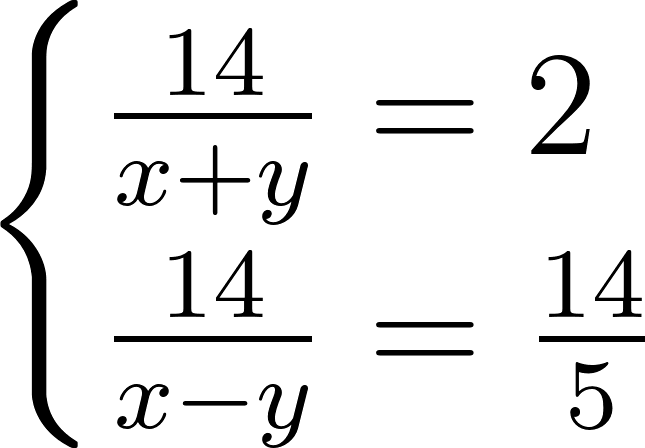
Умножим левые и правые части обоих уравнений на \(\frac{1}{14}\). Получим:
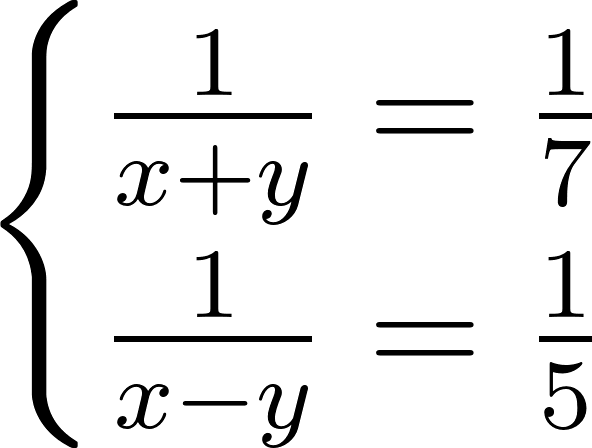
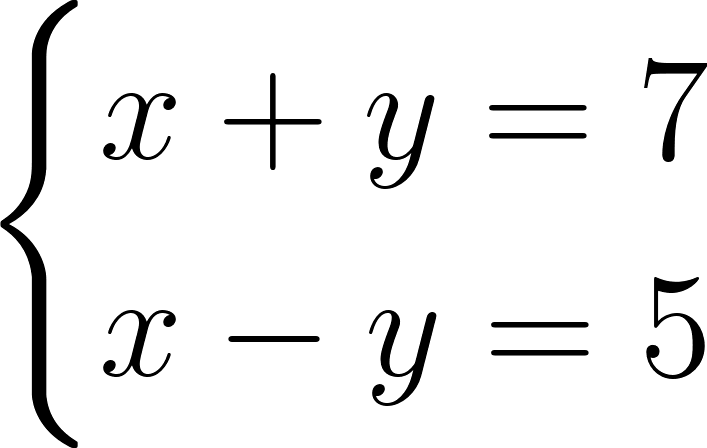
Получили простую систему уравнений, которую легко решить способом сложения. Сложив уравнения, входящие в систему, получим уравнение \(2x = 12\) с одним неизвестным, из которого получается, что \(x = 6\). Следовательно, \(y = 1\). Значит, скорость катера в стоячей воде — 6 км/ч, а скорость течения реки — 1 км/ч.
Подведем итог
Системы уравнений — это записи, состоящие из нескольких уравнений, расположенных одно под другим и объединенных слева фигурной скобкой. Они представляют собой совокупность всех решений, которые являются подходящими для каждого уравнения системы.
Системы можно решать с помощью метода подстановки, метода сложения или используя график. Кроме того, системы уравнений позволяют решать задачи.