Теория вероятностей — важный инструмент, который помогает создавать случайные числа для симуляций и криптографии, улучшать алгоритмы и структуры данных, а еще — разрабатывать точные модели для машинного обучения.
Вместе с Ильей Котовым, специалистом по Data Science в МТС Big Data, разбираемся в основных понятиях теории вероятностей и рассказываем, где и как ее используют.
Что такое теория вероятностей
Теория вероятностей — это раздел математики, который изучает случайные события и ищет в них закономерности.
Она использует математические модели для описания случайных процессов, таких как розыгрыш лотереи или изменение погоды. С ее помощью специалисты могут анализировать и предсказывать исходы в условиях неопределенности.
Разберем основные понятия теории вероятностей.
Вероятность
Это числовая мера, которая показывает степень вероятности того, что произойдет конкретное событие. Она выражается числом от 0 до 1, где 0 — событие невозможно, 1 — событие обязательно случится.
Например, при броске монеты вероятность выпадения каждой из сторон составляет 0,5, или 50%.
Случайное событие
Это возможный исход случайного эксперимента, который может произойти или нет. Такой эксперимент — это событие или действие, результат которого нельзя точно предсказать из-за влияния случайных факторов.
Например, вероятность выпадения осадков метеорологи определяют, анализируя статистические данные.

Распределения вероятностей
Показывают, с какой вероятностью могут произойти разные исходы случайного события.
Существуют разные математические модели, или типы распределений, которые описывают эту вероятность. Выбор конкретного типа зависит от того, какие данные анализируются или какая ситуация моделируется. Они делятся на две группы: дискретные и непрерывные.
Дискретные распределения
Используются для описания событий, у которых определенное количество возможных исходов. То есть когда результаты события можно перечислить по пунктам.
Пример: бросок игральной кости может дать один из шести возможных результатов — от 1 до 6. Каждый результат можно четко определить и посчитать.
Примеры дискретных распределений:
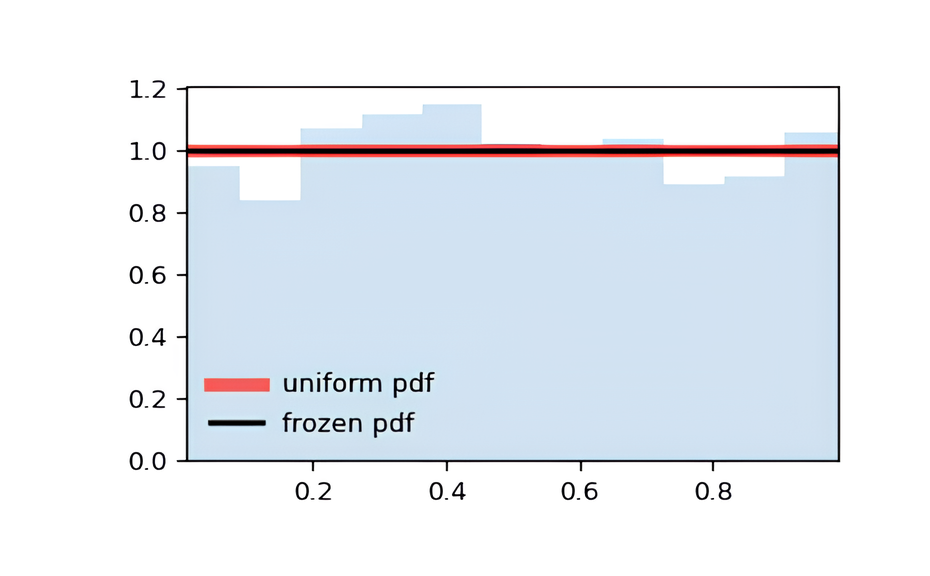
Равномерное распределение — одно из самых простых распределений, при котором у всех исходов одинаковая вероятность.
Например, при бросании монеты вероятность выпадения орла или решки равна 0,5.
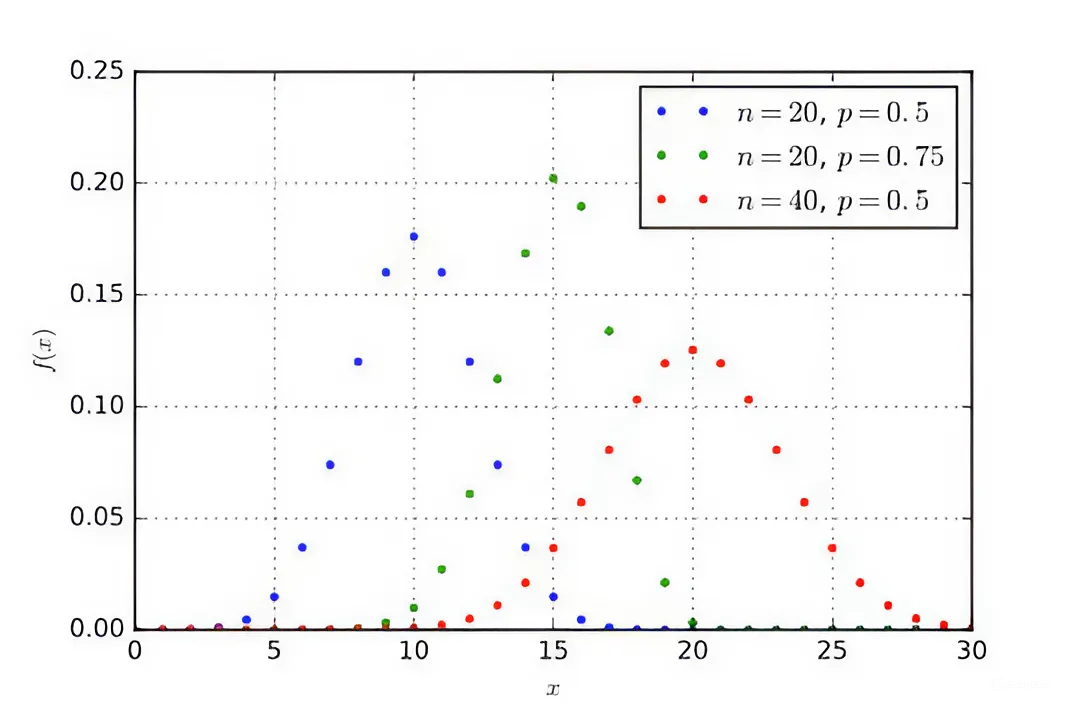
Биномиальное распределение — используется для моделирования числа успешных исходов в серии независимых испытаний с двумя возможными исходами: успех или неудача.
Пример: вероятность того, что при бросании монеты орел выпадет 3 раза из 5.
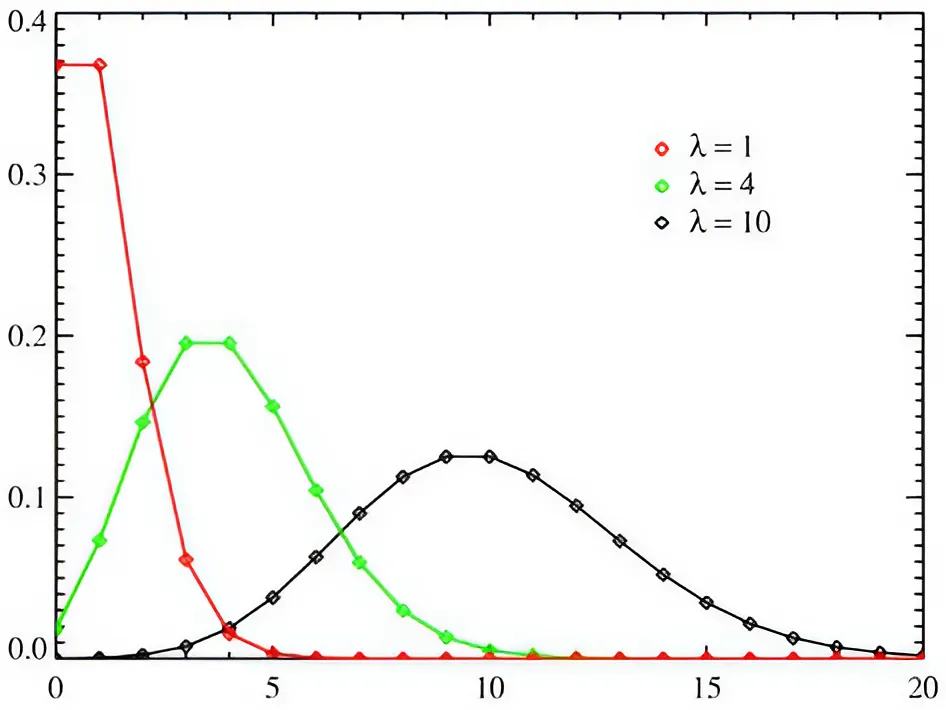
Пуассоновское распределение — применяется для определения вероятности того, сколько раз произойдет определенное событие за фиксированный период времени или в определенном пространстве.
Это распределение используется, когда события случаются независимо друг от друга и с постоянной средней частотой.
Пример — сколько звонков поступит в колл-центр за час.
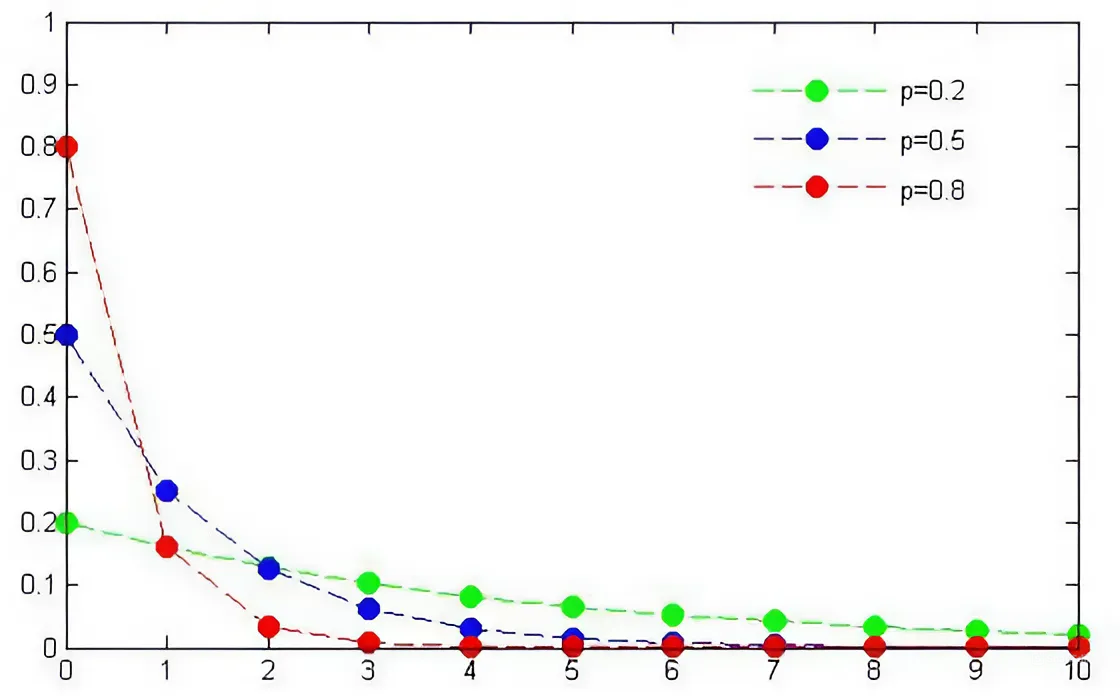
Геометрическое распределение — описывает, сколько требуется попыток для достижения первого успеха. При этом вероятность успеха должна быть одинаковой.
Например, сколько раз нужно бросить монету до первого выпадения орла.
Непрерывные распределения
Используются для описания событий, у которых может быть бесконечно много исходов. В непрерывном распределении нельзя точно перечислить все возможные результаты, потому что они не ограничены конкретными значениями, а могут быть любым числом в заданном промежутке.
Эти распределения применяют для анализа данных и моделирования ситуаций, где результаты измеряются непрерывными величинами, такими как вес, рост, время, температура и т.д.
Примеры непрерывных распределений:
Нормальное (гауссово) распределение — данные распределяются по форме колокола. Большинство значений сгруппированы вокруг среднего.
Например, если взять рост людей, то у большинства он будет около среднего, а очень высоких или очень низких людей будет мало.
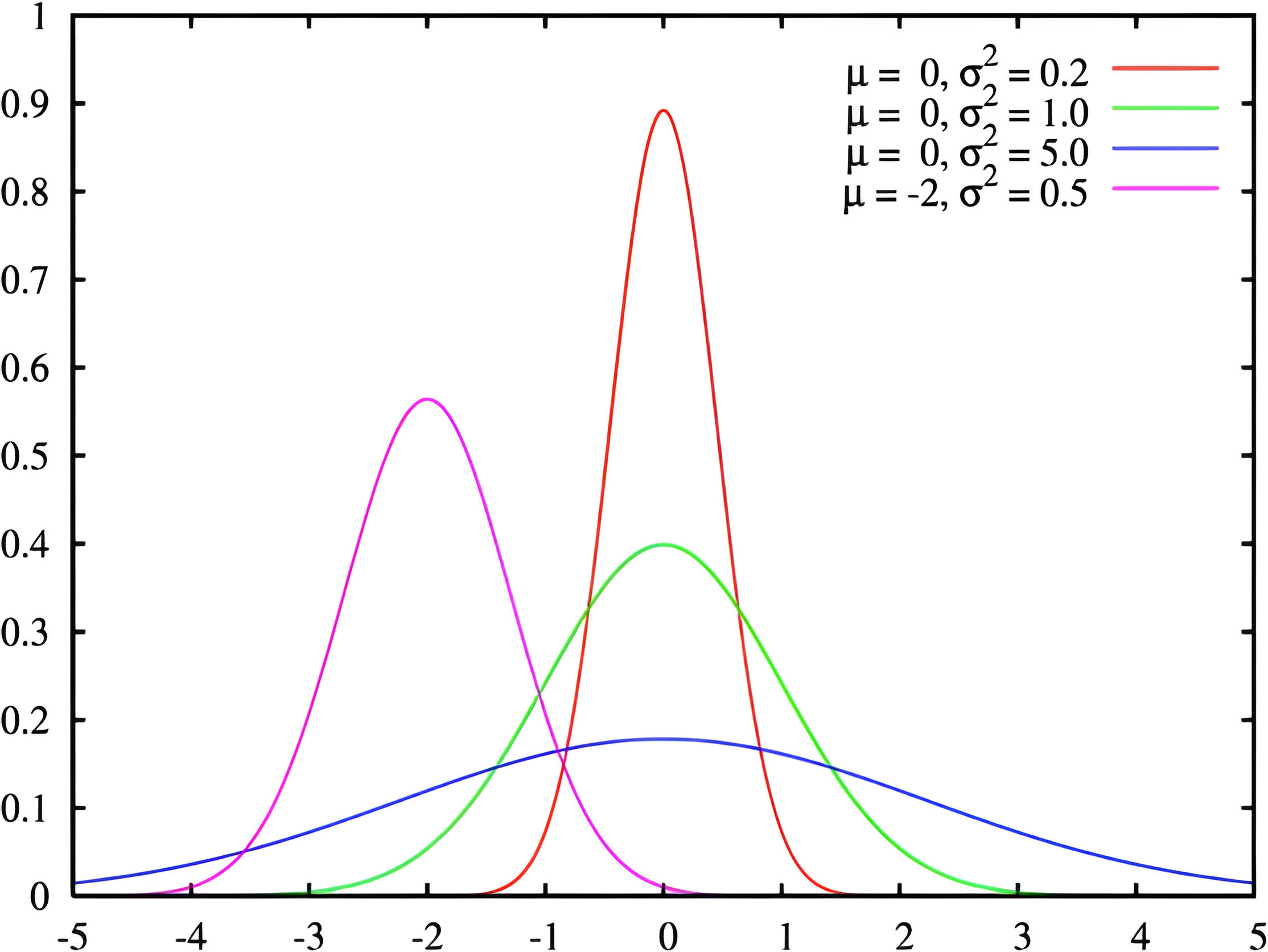
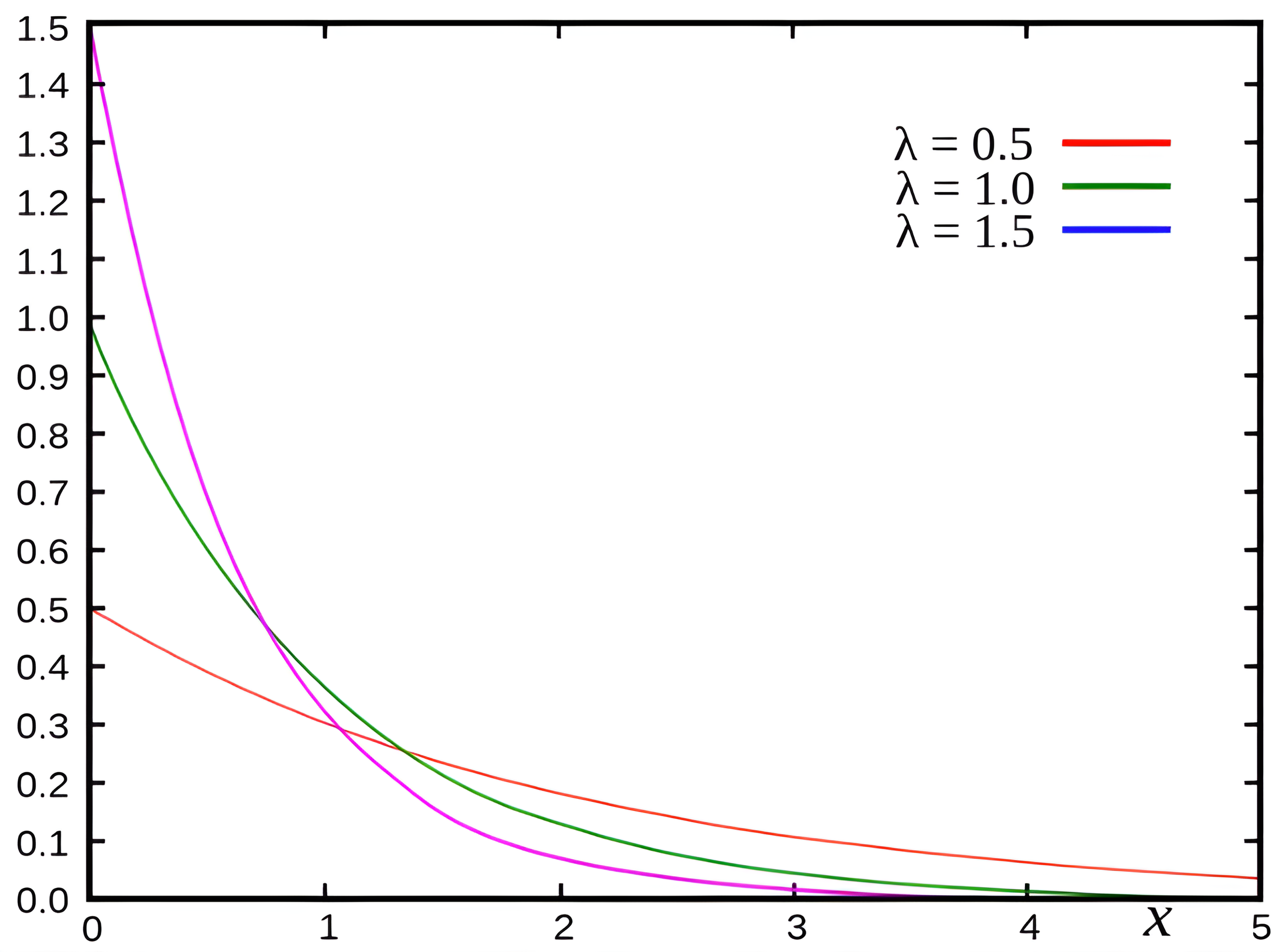
Экспоненциальное распределение — форма гауссова распределения, в которой данные описывают время между событиями, которые происходят с постоянным средним интервалом.
Например, среднее время поездки автобуса из одного пункта в другой.
Случайная величина
Переменная, которая принимает одно значение в зависимости от результата случайного эксперимента. Может быть дискретной или непрерывной:
- Дискретная — принимает конечное или бесконечное количество отдельных значений. К примеру, количество студентов на курсе — всегда целое число.
- Непрерывная — может принимать любые значения в определенном диапазоне. Например, площадь участка, которая тоже может быть измерена с любой степенью точности: километры состоят из метров, метры из сантиметров и т. д.
Для представления результата случайной величины нужны случайные числа. Процесс их создания называется генерацией.
Генерация случайных чисел делится на два основных типа:
- Истинно случайные числа создаются с помощью специальных устройств, которые используют непредсказуемые физические процессы: атмосферный шум, радиоактивный распад и так далее.
Например, инструкция процессоров Intel — RDRAND генерирует числа с помощью теплового шума в электронных компонентах.
- Псевдослучайные числа генерируются алгоритмами и кажутся случайными, но могут быть воспроизведены, если известно исходное значение, или «семя», seed.
Пример — линейный конгруэнтный генератор, который широко используется для моделирования и статистики, но не подходит для криптографии из-за своей предсказуемости.
Какие языки программирования используют для работы с теорией вероятностей
Python
Python — один из самых популярных языков для работы с теорией вероятностей. Он простой в использовании и содержит множество библиотек и фреймворков, с помощью которых можно легко работать с вероятностными и статистическими моделями.
Основные библиотеки:
- NumPy — базовые математические и статистические функции;
- SciPy — продвинутые математические и статистические функции;
- Pandas — работа с табличными данными и временными рядами;
- Matplotlib и Seaborn — визуализация данных;
- Statsmodels — статистическое моделирование;
- Scikit-learn — машинное обучение и моделирование.
R
R специально разработан для статистического анализа и визуализации данных.
Основные библиотеки:
- dplyr и data.table — работа с данными;
- ggplot2 — визуализация данных;
- caret — машинное обучение.
MATLAB
MATLAB используют в инженерии и научных исследованиях для математических вычислений. Он содержит разные функции для расчета вероятностей, статистического анализа и машинного обучения. Это коммерческая платформа, которую можно использовать при покупке дорогой лицензии, поэтому начинающим программистам лучше рассмотреть более доступные варианты.
Основной инструмент — библиотека для статистического анализа и машинного обучения Statistics and Machine Learning Toolbox.
Где применяют теорию вероятностей
Криптография
Теория вероятностей помогает обезопасить данные от взлома. Вот несколько способов, как она используется:
- Создание ключей. С помощью генерации случайных чисел можно создавать уникальные и надежные ключи для шифрования сообщений.
- Проверка случайности. Для проверки безопасности ключей используют вероятностные тесты. Если ключ проходит их — значит, его трудно предсказать.
- Протоколы обмена ключами. При передаче ключей через интернет применяют методы, которые защищают ключи, даже если их перехватят злоумышленники.
Шифрование и дешифрование. С помощью теории вероятностей создают алгоритмы, которые изменяют данные так, что без правильного ключа их невозможно прочитать.
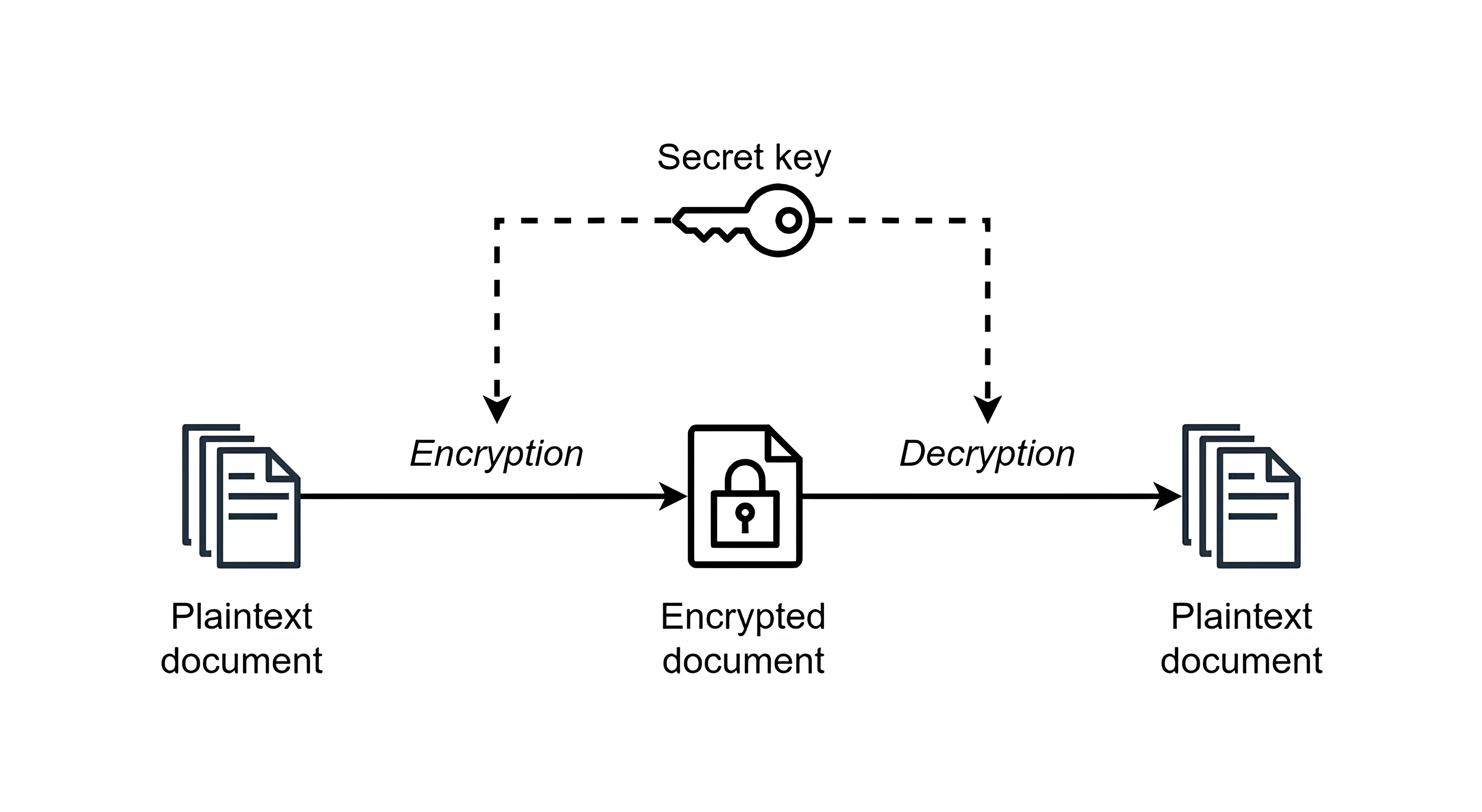
Шифрование и дешифрование. Источник
Машинное обучение
Теорию вероятностей используют в машинном обучении с подкреплением, чтобы найти лучшие способы действий в среде, где результаты непредсказуемы.
Пример — обучающая среда CoinRun. В ней модель испытывает разные стратегии, чтобы научиться достигать целей, например собирать монеты.

Вероятностные модели также могут предсказывать результаты тех или иных действий на основе входных данных, а еще оценивать принадлежность объекта к определенному классу и распознавать речь.
Как это работает: например, системы распознавания речи моделируют последовательность звуков как серию состояний с вероятностными переходами между ними. Так система учится предсказывать следующий звук на основе предыдущих.
Анализ данных и Data Science
Анализ данных пользователей в социальных сетях. Теория вероятностей помогает изучать поведение людей в интернете, чтобы понять, как они взаимодействуют друг с другом и какой контент будет им интересен.
Например, с помощью модели случайного блуждания можно понять, как информация перемещается от одного пользователя к другому.
Прогнозирование временных рядов в бизнес-аналитике. Это методы анализа данных, которые предсказывают будущие цены или значения таких инструментов, как акции, облигации или валюты, на основе их прошлых показателей. К ним относятся, например, модель ARIMA и метод Монте-Карло.
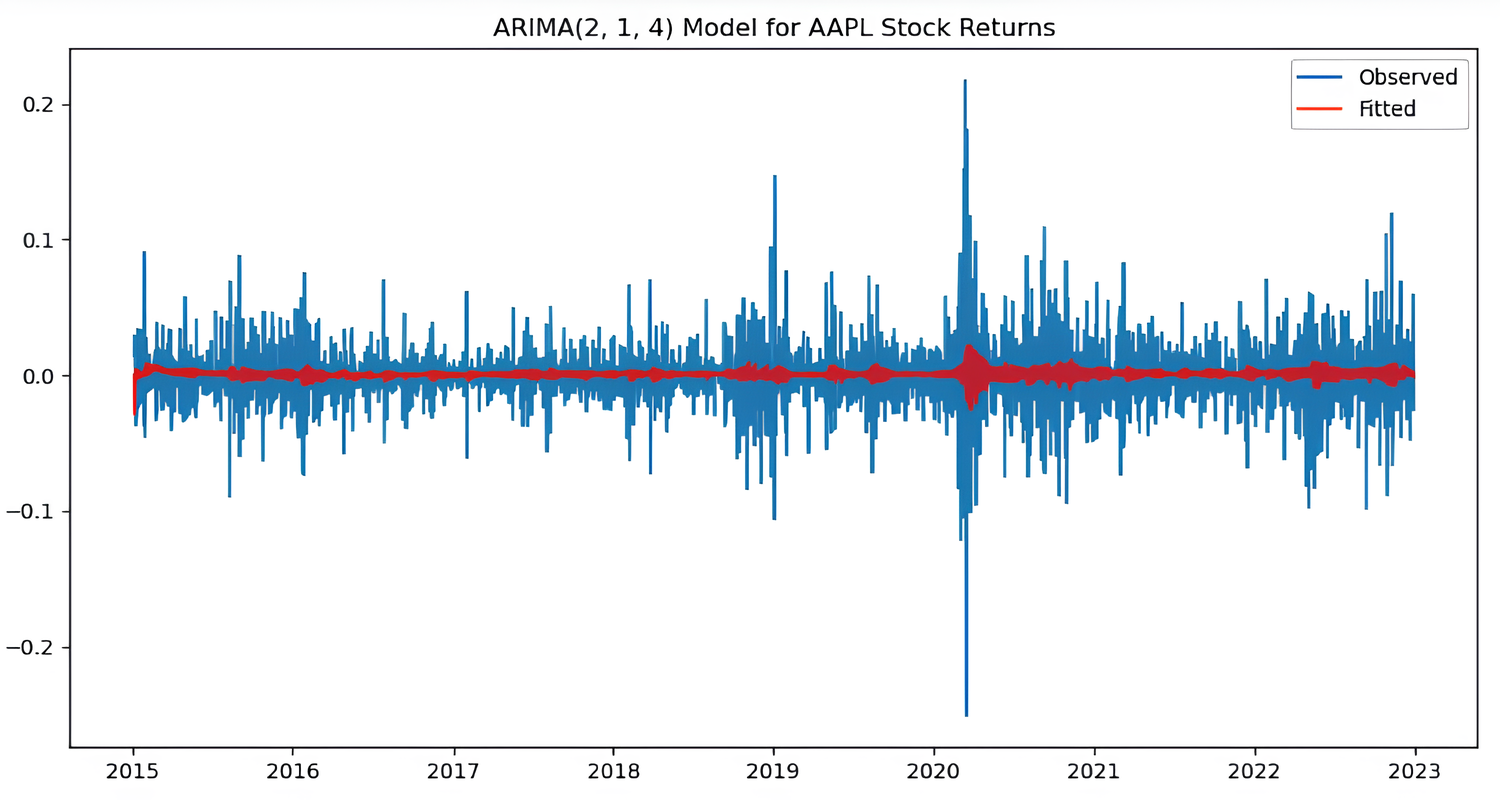
Анализ активности клиентов в онлайн-ритейле. Отслеживание действий клиентов на сайте помогает улучшить опыт пользования сайтом и увеличить продажи. Так, например, модель логистической регрессии оценивает вероятность того, что покупатель купит определенный товар.
Видеоигры
Многие игры используют случайные числа, чтобы сделать события непредсказуемыми, например: появление врагов, выпадение предметов или случайные игровые сценарии. Для этого применяют генератор псевдослучайных чисел.
Такие события могут быть случайными еще до того, как игрок примет решение. К примеру, расположение объектов в играх-песочницах. Другие случайные события происходят после того, как игрок сделал выбор. Например, шанс попасть по врагу или увернуться от атаки.
Как изучить теорию вероятностей
Глубокие знания по теории вероятностей можно получить в университетах. Сложные темы, такие как случайные процессы и моделирование, обычно изучают на технических и экономических факультетах. Во время учебы студенты не только узнают основы теории, но и учатся работать с данными, что важно для работы в области искусственного интеллекта.
Также учеба в вузе — это возможность поучаствовать в научных проектах. Это помогает лучше понять предмет и получить опыт для будущей карьеры в науке и технологиях.
Полезные материалы по теме:
- Probability and Statistics, Khan Academy — бесплатный курс от «Академии Хана» с интерактивными видео и викторинами. Он состоит из 16 модулей и включает такие темы, как условная вероятность, комбинаторика, распределение вероятностей, описательная статистика.
- Introduction to Probability, Dimitri P. Bertsekas and John N. Tsitsiklis — Вводное пособие на английском языке, которое используют в Массачусетском технологическом институте. Здесь описаны как основы теории вероятностей: вероятностные модели, дискретные и непрерывные случайные величины, так и более продвинутые темы, например байесовский вывод, теоремы Бернулли и Пуассона.
- «Теория вероятностей и математическая статистика», Н. Ш. Кремер — учебник по основам теории вероятностей и математической статистики с руководством по решению задач. Есть примеры использования в моделях финансового рынка и производственных процессах.
Коротко о теории вероятностей
- Теория вероятностей изучает закономерности случайных событий. Она помогает анализировать и предсказывать разные исходы в условиях неопределенности.
- Основные понятия теории вероятностей: вероятность, случайное событие, распределение вероятностей и случайная величина.
- Существуют разные математические модели, или типы распределений, которые описывают вероятности, которые используют в зависимости от задачи. Основные — дискретные и непрерывные.
- Генерация случайных чисел делится на два основных типа: истинно случайные и псевдослучайные числа. Первый способ основан на физических процессах: атмосферный и тепловой шум, радиоактивный распад и т. д., а второй использует специальные алгоритмы.
- Самый популярный язык для работы с теорией вероятностей — Python. Он простой и удобный в использовании и содержит большое количество библиотек и фреймворков.
- Программисты сталкиваются с теорией вероятностей при работе в сферах криптографии, машинного обучения, Data Science, разработки видеоигр.








