Алгоритм Дейкстры

Алгоритм Дейкстры — это метод, который находит кратчайший путь от одной вершины графа к другой. Граф — структура из точек-вершин, соединенных ребрами-отрезками. Его можно представить как схему дорог или как компьютерную сеть. Ребра — это связи, по ним можно двигаться от одной вершины к другой.

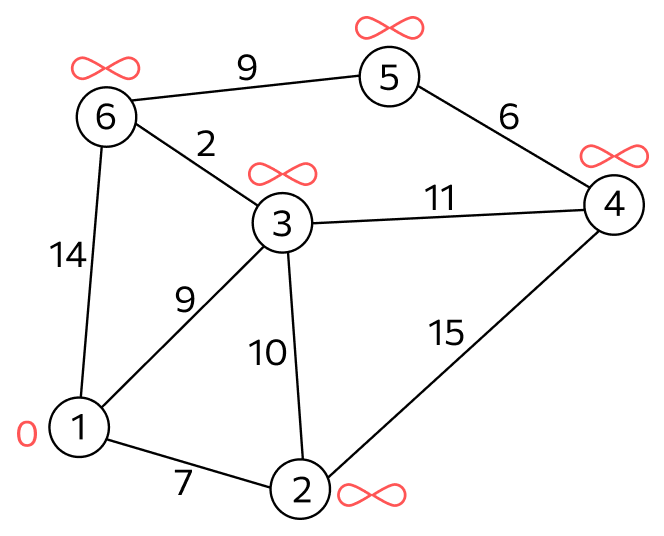
Графы используют для моделирования реальных объектов, а алгоритмы поиска пути — при их изучении, а также решении практических задач. Алгоритм Дейкстры работает для графов, у которых нет ребер с отрицательным весом, т.е. таких, при прохождении через которые длина пути как бы уменьшается.

В отличие от похожих методов, алгоритм Дейкстры ищет оптимальный маршрут от одной заданной вершины ко всем остальным. Попутно он высчитывает длину пути — суммарный вес ребер, по которым проходит при этом маршруте.

Кто пользуется алгоритмом Дейкстры

• Математики и другие ученые, которые пользуются графами как абстрактными единицами. Задача поиска маршрута в науке может быть и чисто фундаментальной, и прикладной.
• Дата-сайентисты. В этой области много математики, в том числе активно используется теория графов.
• Сетевые инженеры, так как алгоритм Дейкстры лежит в основе работы нескольких протоколов маршрутизации. Сама по себе компьютерная сеть представляет собой граф, поэтому специалисты по сетям должны знать, что это такое.

Зачем нужен алгоритм Дейкстры

Основная задача — поиск кратчайшего пути по схеме, где множество точек соединено между собой отрезками. В виде такой схемы можно представить многие объекты реального мира, поэтому практических примеров использования алгоритма много:

• автоматическое построение маршрута на онлайн-карте;
• поиск системой бронирования наиболее быстрых или дешевых билетов, в том числе с возможными пересадками;
• моделирование движения робота, который перемещается по местности;
• разработка поведения неигровых персонажей, создание игрового ИИ в геймдеве;
• автоматическая обработка транспортных потоков;
• маршрутизация движения данных в компьютерной сети;
• расчет движения тока по электрическим цепям.

Как работает алгоритм

Алгоритм Дейкстры пошаговый. Сначала выбирается точка, от которой будут отсчитываться пути. Затем алгоритм поочередно ищет самые короткие маршруты из исходной точки в другие. Вершины, где он уже побывал, отмечает посещенными. Алгоритм использует посещенные вершины, когда рассчитывает пути для непосещенных.

Это может звучать сложно, поэтому мы хотим показать вам, как это выглядит на примере. Возьмем такой граф: цифрами в кружках обозначены вершины, а числа возле ребер — это вес путей между ними.

Инициализация. Пусть вершиной, из которой мы будем считать маршруты, будет 0. Расстояние до самой себя у этой вершины логично равно нулю. Остальные мы пока не знаем, поэтому отметим символом бесконечности.

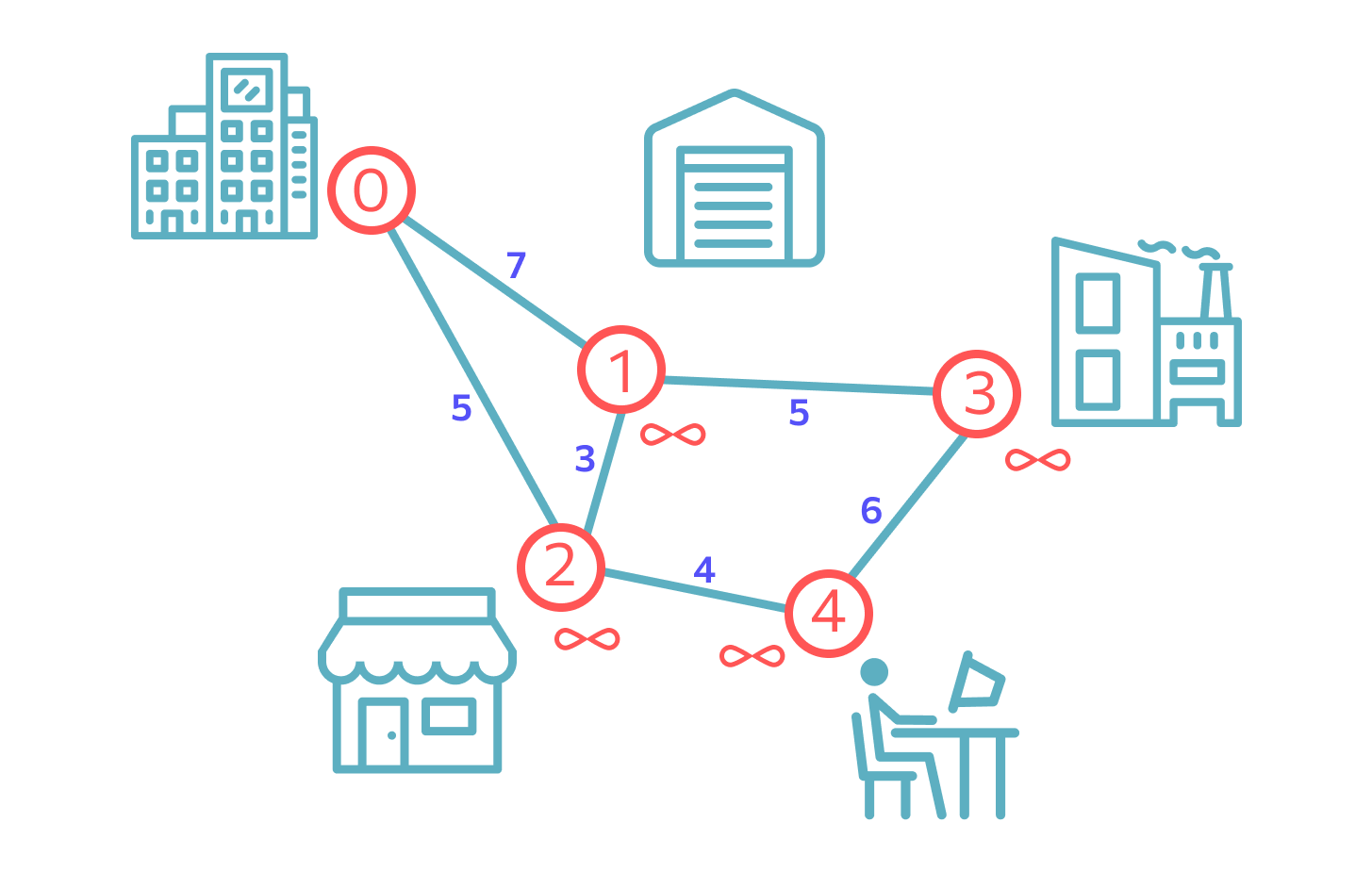
Расстояние от 0 до 0 помечаем равным нулю, а саму вершину — посещенной.

Первый шаг алгоритма. Мы выбираем еще не посещенную вершину с самой маленькой меткой относительно исходной — то есть такую, которая находится ближе всех. На первом шаге это одна из соседних вершин — та, которая соединена с исходной самым «маленьким» ребром.

Для графа, который мы рассматриваем, это точка 2. Мы выбираем ее, «переходим» в нее и смотрим уже на ее соседей.

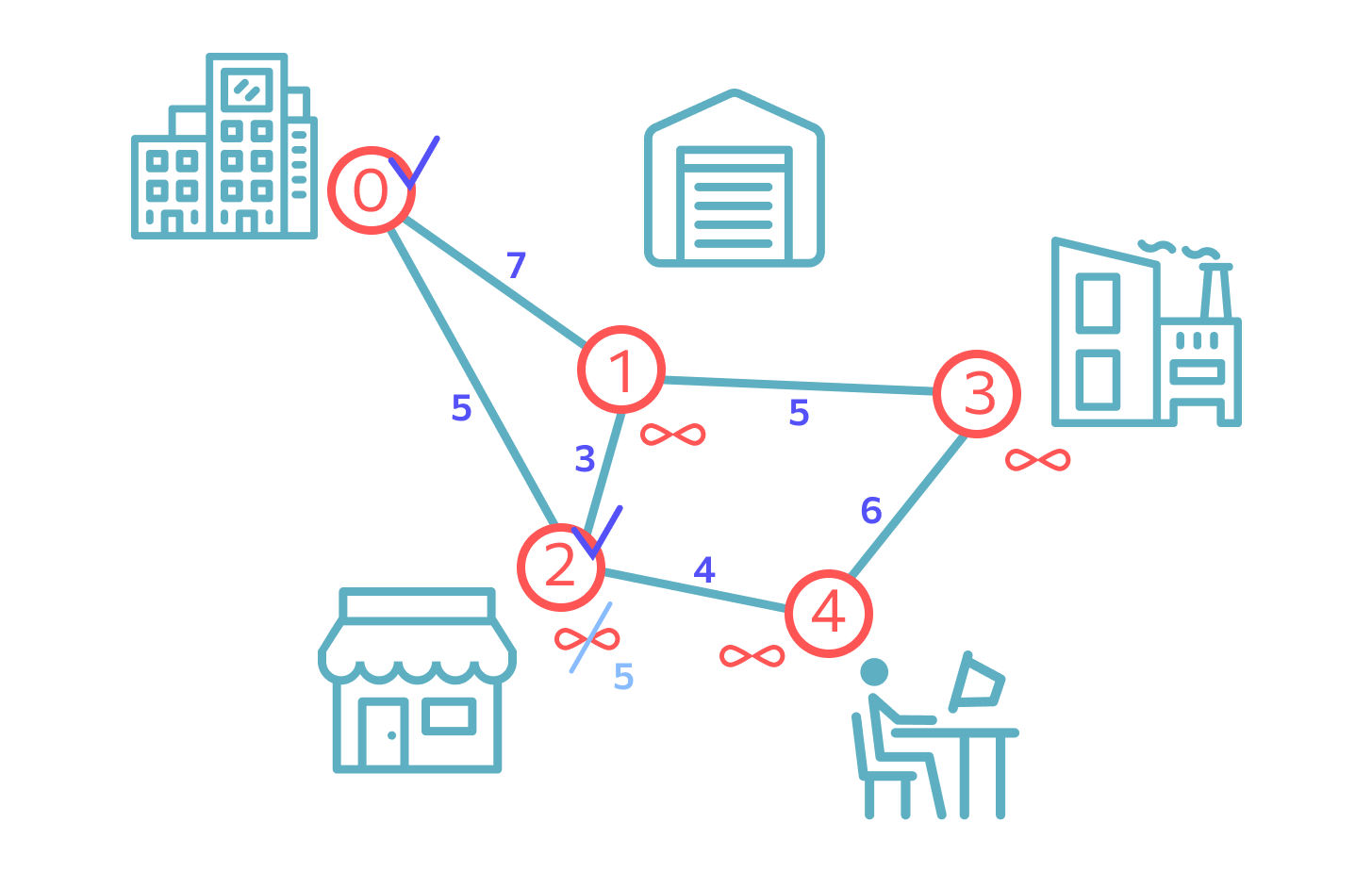
Дальнейшие шаги алгоритма. Для выбранной точки нужно осмотреть соседей и записать длину пути до них с учетом пройденного пути. А потом выбрать ближнюю точку. Но есть нюанс: нужно учитывать точки, которые мы уже использовали в прошлый раз. Если они дают более «выгодный» путь, лучше воспользоваться ими.

Например, на выбранном графе есть точка 1. В нее можно перейти из точки 2, где мы находимся. Но этот путь будет длиннее, чем при переходе напрямую из точки 0, а ведь она для нас исходная. Поэтому «короткий путь» для точки 1 — это маршрут 0–1. Отмечаем вершину посещенной.

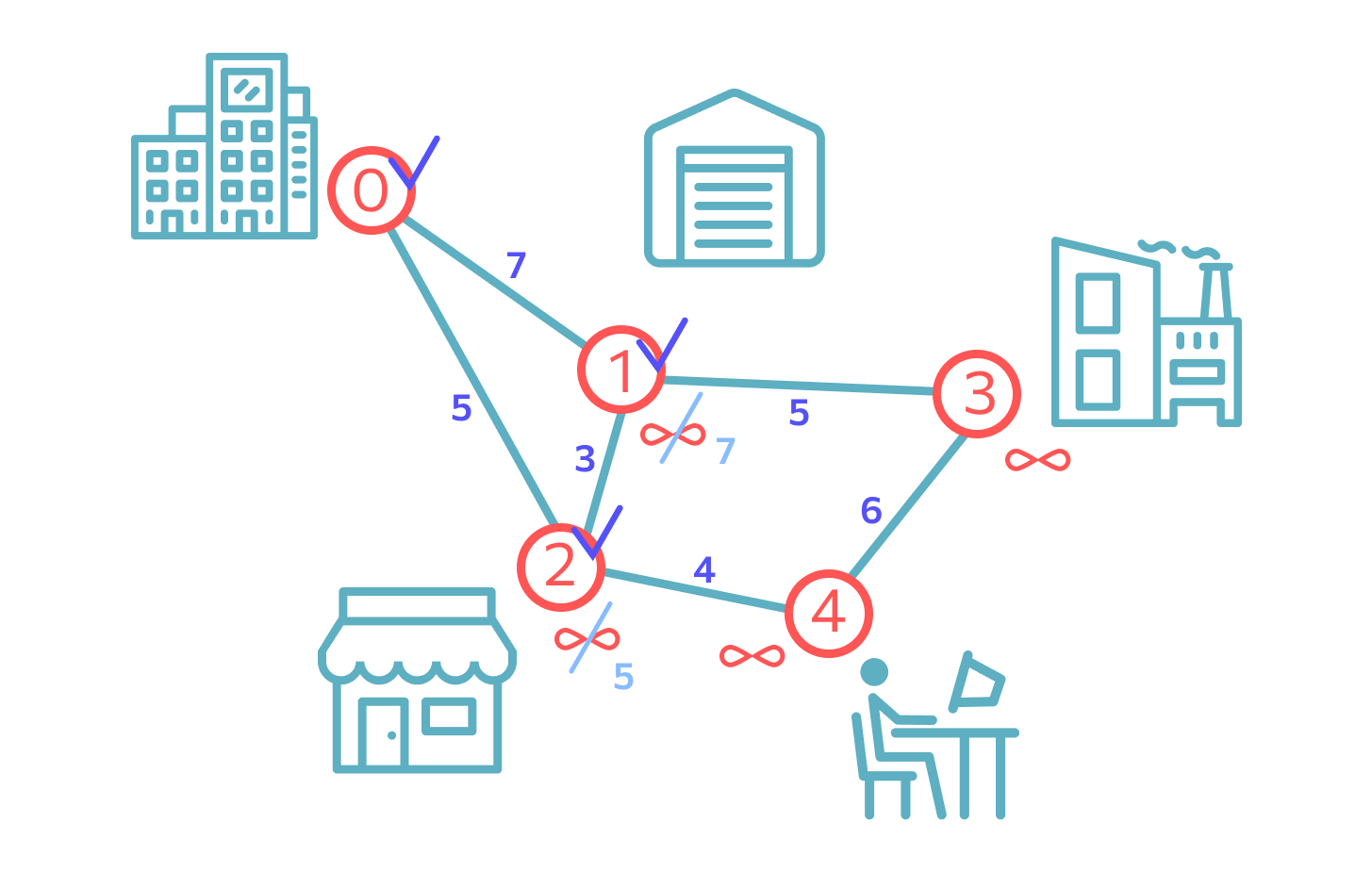
Шаги повторяются, пока на графе есть непосещенные точки. Если вершину не посетили, она не участвует в расчетах. Если после ее «открытия» появился новый, более короткий путь к какой-либо точке, то минимальное расстояние для нее перезаписывается.

Конец алгоритма. Когда непосещенные вершины заканчиваются, алгоритм прекращает работу. Результат его действия — список кратчайших маршрутов до каждой точки из исходной. Для каждого маршрута указана его длина.

Мы говорим «длина», но это условно. Например, при поиске билетов в роли веса ребра может выступать их цена, а при организации электрической цепи — расход электроэнергии.

Теория графов — обширная отрасль дискретной математики. Ее используют во множестве сфер, от химии до разработки. В профильных университетах теорию графов изучают на курсе дискретной математики. Также получить базу знаний и решать практические задачи под контролем наставника можно на курсах SkillFactory.