Числа Фибоначчи

Простыми словами, числа Фибоначчи (строка или ряд Фибоначчи) — числовая последовательность, первые два числа которой являются 0 и 1, а каждое последующее за ними число является суммой двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13 и так далее. Такое построение еще часто называют «законом Фибоначчи» или «принципом Фибоначчи». Представляет собой частный пример линейной рекуррентной последовательности (рекурсии).

Эту последовательность впервые описал итальянский математик Леонардо Пизанский в его работе «Жизнь абака» в 1202 году. Закономерность, описываемая числами Фибоначчи, приобрела популярность в эпоху Возрождения и особенно Нового времени, где повлияла на самые разные стороны жизни — от фундаментальной и прикладной математики до искусства и архитектуры.

Как появились числа Фибоначчи: кролики и формула

Сам Леонардо Пизанский (Фибоначчи — его прозвище) предложил знаменитую последовательность в виде «задачи о кроликах», где описал кроличью популяцию со следующими условиями:

• В начале 1 месяца появляется первая пара кроликов (самец и самка).
• Со 2 месяца кролики начинают ежемесячно производить новую пару.
• Кролики бессмертны.

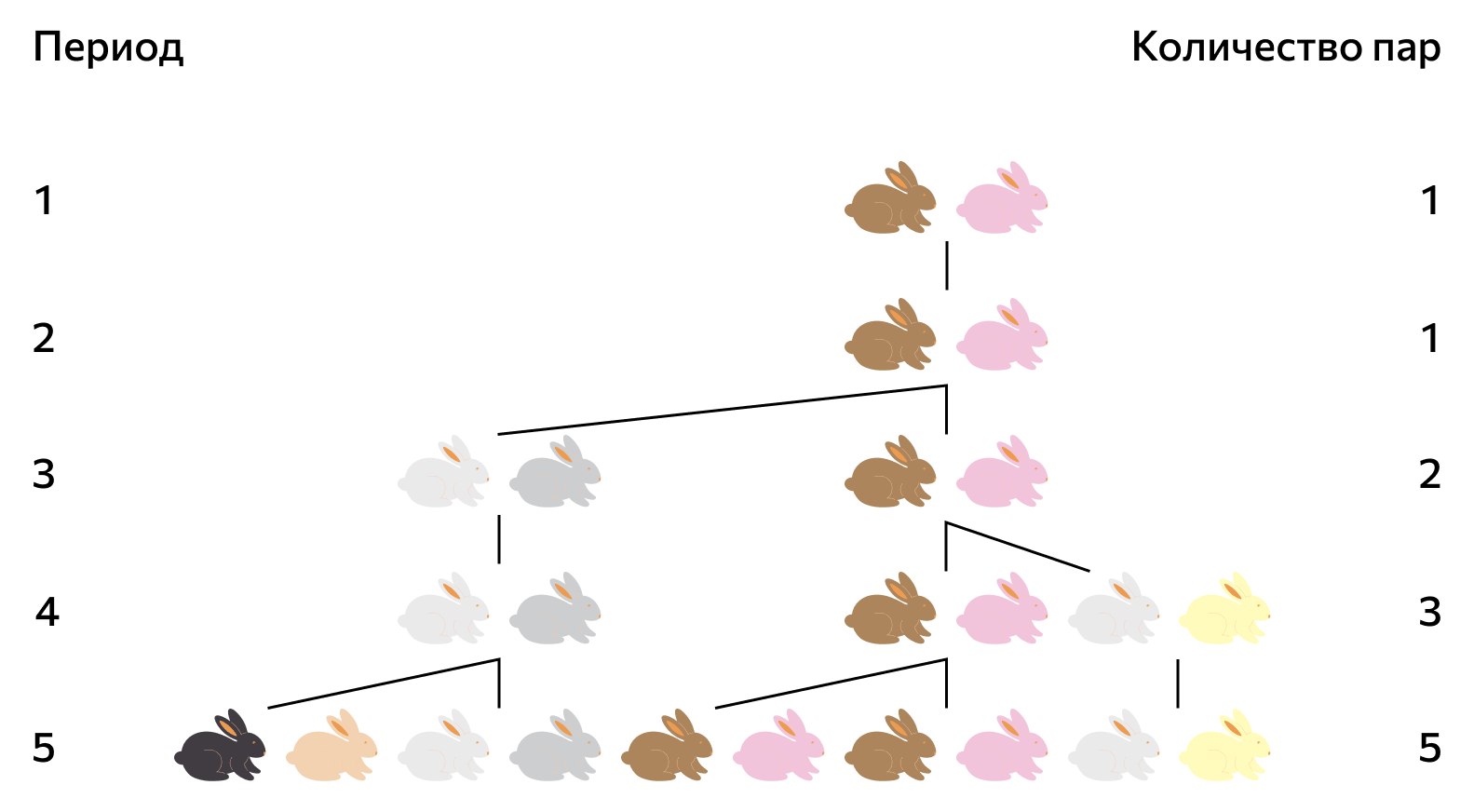
Задача состояла в том, чтобы рассчитать, сколько кроликов в популяции будет через год. Математически ее решение описывается формулой:

Fn = Fn–2 + Fn–1, где F0=0, F1=1, а n — больше или равно 2 и является целым числом.

Рассчитанная по этой формуле последовательность выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … .

Сам Фибоначчи рассматривал эту последовательность просто как одно из математических упражнений среди прочих задач, указанных в его книге «Жизнь абака». Пример с кроликами был идеальной моделью, в которой кролики размножались строго каждый месяц, производили только двух крольчат разного пола и при этом сами не умирали. Однако некоторые современные исследователи называют ее первой в истории популяционной моделью.

Таблица чисел Фибоначчи

n	F(n)
0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13
8	21
9	34
10	55
11	89
12	144
13	233
14	377
15	610
16	987
17	1 597
18	2 584
19	4 181
20	6 765

Сама последовательность была известна еще с древних времен — в частности, она использовалась в древнеиндийском стихосложении, в том или ином виде ее знали древнегреческие и арабские математики. Заслуга именно Фибоначчи была в том, что он популяризировал ее в западноевропейской математике, а также ввел в европейскую науку позиционную систему счисления (известную народам Востока), которая имела краеугольное значение в последующем развитии математических наук.

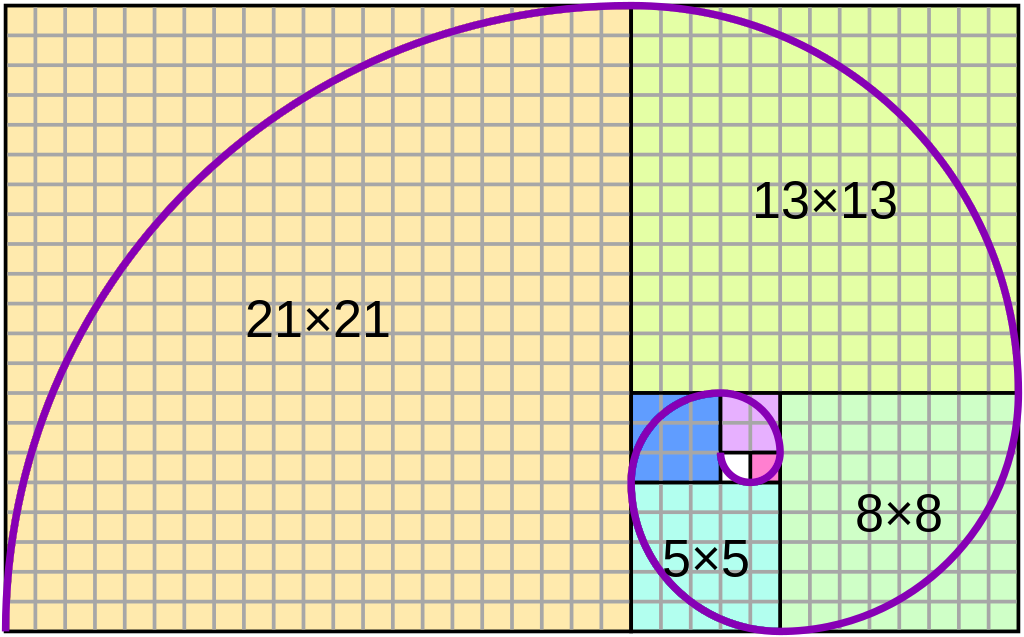
Визуальным воплощением этой последовательности является золотая спираль. Она представляет собой дуги окружностей, вписанных в квадраты, размеры которых соотносятся друг с другом как числа в строке Фибоначчи. В основе этой фигуры лежит золотое сечение — идеальная пропорция, равная 0,61803. Золотая спираль стала одним из распространенных принципов математического пропорционирования, который широко используется в искусстве, архитектуре, начиная с эпохи Возрождения и по сегодняшний день.

Сумма чисел Фибоначчи

Кривая Фибоначчи обладает простой и наглядной закономерностью: сумма первых n чисел равна следующему числу Фибоначчи минус 1.

Формула суммы чисел в ряде Фибоначчи выглядит так:

F₀ + F₁ + F₂ + … + Fₙ = Fₙ₊₂ − 1

Такая связь позволяет быстро вычислять сумму, не складывая элементы по одному. Например, сумма первых пяти чисел (0, 1, 1, 2, 3) равна 7, и это совпадает с F₇ − 1 = 13 − 6 = 7.

Эта закономерность полезна при оценке роста процессов, описываемых числами Фибоначчи: прироста популяций в математических моделях, структуры рекурсивных алгоритмов или количества операций в вычислительных задачах.

Применение ряда чисел Фибоначчи в информатике и программировании

Последовательность Фибоначчи — один из классических примеров рекурсии в математике. Рекурсией называется функция, определяющая свое значение через обращение к самой себе. Рекурсивные алгоритмы используются в программировании для упрощения вычислений. Умение обращаться с ними является одним из базовых навыков программиста. Поэтому расчет числа Фибоначчи (достаточно простой рекуррентной функции) часто является тестовым заданием, которое дается соискателю на вакансию программиста для проверки его навыков или применяется в обучении будущих кодеров.

Пример вычисления числа Фибоначчи на Python

Так выглядит рекурсивный поиск чисел Фибоначчи на языке Python:

def fibonacci(n):
    if n in (1, 2):
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

Проблема рекурсивного нахождения чисел Фибоначчи в том, что после определенного предела процесс сильно замедляется. Причина — в самой природе рекурсии: основанная на ней программа постоянно обращается сама к себе. Если число n (номер искомого элемента ряда) большое, обычный компьютер просто не справится или процесс займет слишком много времени.

Поэтому для нахождения чисел Фибоначчи применяются и другие способы — например, обычный цикл (язык Python):

fib1 = fib2 = 1
n = input('Номер элемента ряда Фибоначчи: ')
n = int(n) - 2
while n > 0:
    fib1, fib2 = fib2, fib1 + fib2
    n -= 1
print('Значение этого элемента:', fib2)

Последовательность Фибоначчи и генерация псевдослучайных чисел

Случайными называются числа, полученные в результате случайного события. Простейший пример — подбрасывание монетки или игральной кости. Такие числовые последовательности широко используются в современной науке, например для описания различных природных, социальных, экономических и других процессов с влиянием большого количества различных факторов, делающих результаты трудно- или непредсказуемыми.

Проблема в том, что получить настоящие случайные числа очень сложно. Классические примеры с монеткой, игральными костями и колодой карт дают лишь небольшие величины, чего недостаточно для современной науки и технологий. Теоретически случайные числа можно получить из космического излучения или радиации, из дробового шума в электрических цепях. Однако на практике использовать такие источники невыгодно по следующим причинам:

• Их установка и настройка требуют слишком много времени и труда.
• Генерация случайных чисел с их помощью происходит медленно.
• Воспроизвести ранее полученные результаты на данном уровне развития технологий невозможно.

Практическим решением проблемы получения случайных чисел стали псевдослучайные числа, то есть такие, которые обладают некоторыми их свойствами, но генерируются по заранее заданному алгоритму. Для их получения используются специальные вычислительные программы — генераторы псевдослучайных чисел. Особенность их работы заключается в том, что через определенный период времени генерируемые последовательности начинают повторяться. В некоторых областях информатики, таких как криптография (шифрование), это имеет критическое значение. Поэтому еще в 50-х годах XX века был предложен способ генерации псевдослучайных чисел на основе строки Фибоначчи (метод Фибоначчи с запаздыванием), который позволил повысить степень случайности в числовых последовательностях. Он успешно используется сегодня не только в криптографии, но и в имитационном моделировании различных естественных, социальных, экономических процессов, например:

• В кристаллографии с их помощью можно приблизительно моделировать рост кристаллов.
• В биологии и биоинформатике с помощью чисел Фибоначчи описываются такие процессы и объекты, как расположение листьев и лепестков у растений, семян в сосновых шишках, ячеек в плодах ананаса.
• Некоторые природные процессы, такие как флуктуации в турбулентных потоках или вихревые процессы в атмосфере, можно приблизительно описать числами Фибоначчи.

Числа Фибоначчи в трейдинге

Закономерность, описываемая в сетке Фибоначчи, получила неожиданное применение в биржевой торговле. В 30-х годах прошлого века американский инженер и менеджер Ральф Нельсон Эллиотт провел масштабное исследование фондов и заметил, что их колебания происходят в определенном ритме, в котором прослеживалось все то же золотое сечение — 0,61803. Сам исследователь делал все вычисления и прогнозы вручную, однако сегодня существуют специальные биржевые программы (терминалы), предлагающие несколько инструментов на основе закономерности Фибоначчи: уровни, дуги, веера.

Как пользуются числами Фибоначчи в трейдинге? Для поиска уровней, где цена может остановиться, развернуться или продолжить движение. На основе последовательности строят несколько инструментов технического анализа:

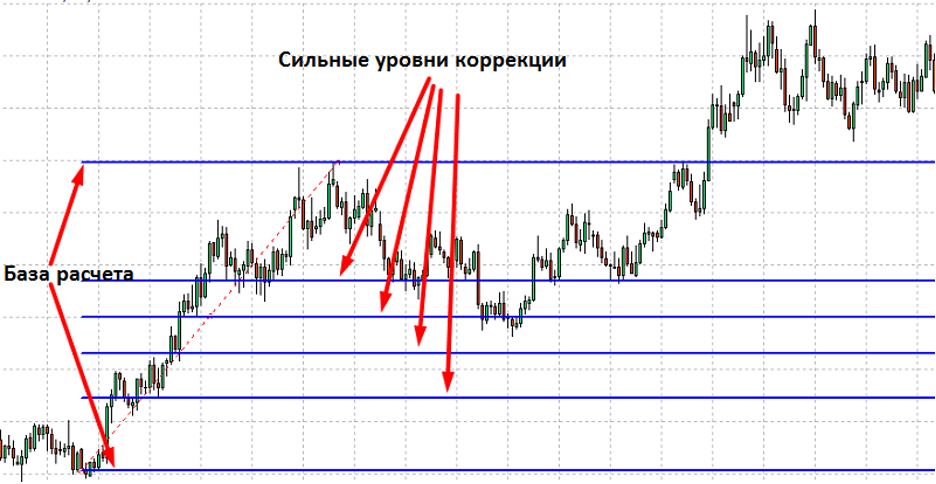
Основные уровни Фибоначчи для трейдинга:

1. Уровни коррекции (Fibonacci retracement).
Трейдеры отмечают на графике два экстремума — локальный максимум и минимум — и получают сетку уровней 23,6%, 38,2%, 50%, 61,8% и 78,6%. Эти уровни показывают глубину возможной коррекции: если цена снижается после роста, ее «типичные» остановки часто совпадают с коэффициентами Фибоначчи.

2. Уровни расширения (Fibonacci extension).
Используются для оценки потенциальных целей после пробоя или окончания коррекции. Популярные уровни — 127,2%, 161,8%, 261,8%. Они помогают спрогнозировать зоны фиксации прибыли.

3. Веер Фибоначчи (Fibonacci fan).
На графике строятся наклонные линии, исходящие из ключевой точки. Они показывают потенциальные линии поддержки и сопротивления при движении тренда.

4. Дуги Фибоначчи (Fibonacci arcs).
Центр ставится в точку разворота, а дуги с радиусом, пропорциональным индикаторам Фибоначчи, помогают оценить скорость коррекции и вероятные зоны реакции цены.

5. Временные зоны Фибоначчи (Fibonacci time zones).
Вертикальные линии делят график по числам Фибоначчи (1, 2, 3, 5, 8 …) и подсказывают моменты, когда может измениться динамика рынка.

Следует отметить, что использование графика Фибоначчи в трейдинге носит спорный характер. Хотя цикличность рынка и фондовых показателей действительно существует, на нее влияет множество факторов, которые невозможно предугадать строгими математическими законами. Тем не менее в ситуации минимального внешнего влияния использование биржевых инструментов, построенных на строках Фибоначчи, действительно позволяет с определенной эффективностью прогнозировать поведение цен, индексов акций.

Числа Фибоначчи в визуальном искусстве и дизайне

Золотая спираль, основанная на последовательности чисел Фибоначчи, является одним из универсальных принципов построения пропорций. Лежащее в ее основе золотое сечение было известно еще в государствах Древнего Востока, но особую популярность оно приобрело в эпоху Возрождения. Великие скульпторы и живописцы того времени начали применять золотую спираль для построения художественной композиции, пропорций различных объектов, в том числе человеческого тела. Золотое сечение сегодня используется как одна из моделей для гармоничного распределения объектов в кадре (в фото- и киноискусстве), элементов плакатов и т.д.

В компьютерную эру золотое сечение (золотая спираль) и числа Фибоначчи также нашли свое применение в визуальном искусстве, в частности, 2D/3D-моделировании и веб-дизайне:

• Решетка Фибоначчи применяется для эффективного наложения точек на двухмерные и трехмерные объекты, например сферу или многогранники. Таким способом можно выполнить высокоточную огранку ювелирных камней или построить визуальную модель молекулярных решеток некоторых веществ.

• На основе числовой последовательности Фибоначчи строится один из вариантов фракталов — самоподобных фигур. Эту математическую модель можно использовать в компьютерной графике для построения ветвящихся объектов (ветвей, корней деревьев, русел рек, кристаллов и т. д.).
• Золотое сечение применяется в веб-дизайне для разметки страниц некоторых сайтов или веб-приложений. Элементы интерфейса, организованные таким способом, образуют визуально привлекательную и удобную рабочую область.
• Фрактальная геометрия, основанная в том числе на закономерности Фибоначчи, является самостоятельным направлением визуального искусства. Она применяется в аудиовизуальных инсталляциях, мэппингах и т.д.

Числа Фибоначчи в природе

Примечательно, что эта математическая закономерность встречается в природе удивительно часто и проявляется в самых разнообразных формах.

Одно из самых известных проявлений чисел Фибоначчи в природе – это спирали. Например, раковины улиток и моллюсков часто следуют спиральной форме, размеры витков которой соответствуют числам Фибоначчи. Подобным образом спирали можно увидеть в цветах подсолнуха и в сосновых шишках. Если посчитать ряды семечек на цветке подсолнуха, можно заметить, что их количество обычно соответствует числам Фибоначчи.

Растения часто демонстрируют ветвление, следующее числам Фибоначчи. Если наблюдать за тем, как растут ветви деревьев или корни, можно заметить, что каждый новый отросток появляется в точках, которые соответствуют числам Фибоначчи. Это помогает растению максимально эффективно использовать пространство и ресурсы, а также получать достаточное количество света и питательных веществ.

Филлотаксис – это расположение листьев на стебле растения. Часто листья располагаются по спирали, и углы между ними соответствуют золотому углу (приблизительно 137,5 градусов), что связано с числами Фибоначчи. Такое расположение позволяет листьям избегать затенения друг друга, обеспечивая равномерное распределение солнечного света и дождевой воды.

Популяции некоторых животных, особенно кроликов, также могут демонстрировать закономерности, связанные с числами Фибоначчи. Например, если считать поколения кроликов при определенных условиях размножения, то количество пар кроликов в каждом поколении будет следовать числам Фибоначчи.

В генетике и биологии числа Фибоначчи также находят свое место. Один из примеров – строение ДНК, которая закручивается в виде двойной спирали. Отношение длин этих спиралей близко к золотому сечению, что также связано с числами Фибоначчи. Строение клеток и распределение их органелл иногда демонстрируют подобные закономерности.

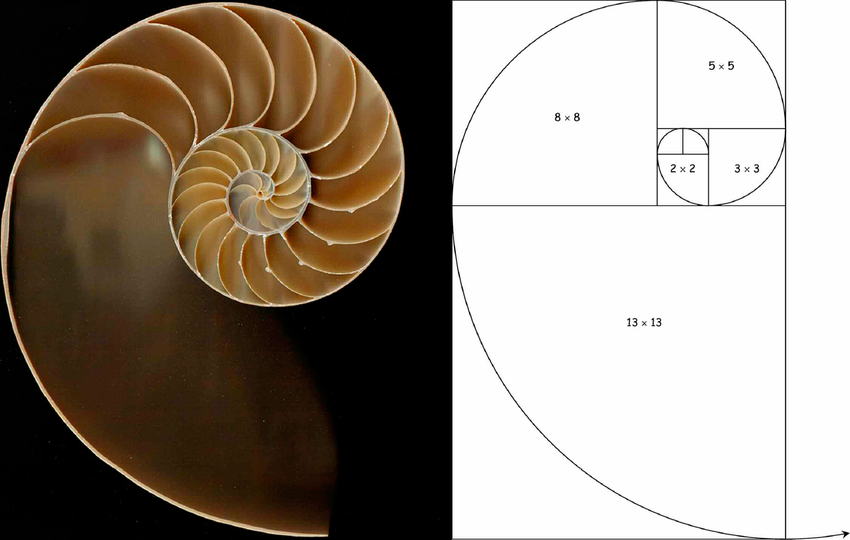
Числа Фибоначчи не просто математическое любопытство. Они являются важным элементом в структуре и функционировании живой природы. Эти числа помогают организму максимально эффективно использовать ресурсы, адаптироваться к окружающей среде и эволюционировать. Их присутствие в природе подчеркивает глубокую связь между математикой и биологией, демонстрируя, как фундаментальные принципы могут быть воплощены в самых разных формах жизни.

Как построить спираль Фибоначчи

Спираль, часто называемая «золотой спиралью», является визуальным воплощением Последовательность Фибоначчи и связанного с ней Золотое сечение. В основе — квадраты с размерами, равными членам последовательности: 1, 1, 2, 3, 5, 8 и далее. На этих квадратах затем строятся дуги окружностей, которые формируют плавную завитушку-спираль. Ниже — пошаговое руководство.

Шаг 1. Построить серию квадратов по размерам членов последовательности

1. Выберите начальное число (например, 1 × 1).
2. Приложите к нему ещё один квадрат того же размера (еще 1 × 1) рядом.
3. Далее, построите квадрат размера 2 × 2 (1+1), примыкающий к двум предыдущим.
4. Потом квадрат 3 × 3 (1+2), потом 5 × 5 (2+3), затем 8 × 8 (3+5) и т.д. — каждый следующий квадрат имеет сторону равную сумме сторон двух предыдущих квадратов (соответствует Fn = F(n-1)+F(n-2)).
5. Все квадраты размещаются так, чтобы они образовывали «лестницу» или «спиральную» цепочку, где каждый новый квадрат примыкает к предыдущей композиции.

Шаг 2. Нарисовать дуги на каждом квадрате

1. Внутри каждого квадрата нужно найти его диагональ или геометрический центр — ориентир.
2. На квадрате с размером 1 × 1 нарисуйте четверть круга (дугу) с центром в одном из углов квадрата и радиусом равным стороне квадрата.
3. Далее на квадрате 2 × 2: также четверть круга, радиус = 2, центр в точке, где примыкает этот квадрат к предыдущим.
4. Продолжайте: каждый следующий квадрат — новая дуга с радиусом, равным стороне квадрата (3, 5, 8 …), дуга проводится от одного угла к другому, таким образом, что все дуги вместе формируют непрерывную завитушку.
5. В результате вы получите плавную спираль, которая «обходит» каждый квадрат по очереди — от малого к большему.

Шаг 3. Проверить и оформить композицию

• Убедитесь, что квадраты расположены последовательно: 1, 1, 2, 3, 5, 8.
• Дуги должны переходить гладко из одного квадрата в следующий, создавая цельную форму.
• При желании можно дополнить рисунок линией, соединяющей концы дуг, чтобы подчеркнуть спираль.
• Чтобы визуально усилить эффект «золотого» пропорционирования, можно подчеркнуть или затемнить границы квадратов и дуг.

Заблуждения, связанные с числами Фибоначчи

Благодаря современной поп-культуре с этой числовой последовательностью связано множество популярных мифов:

• Универсальность. Во многих источниках числа Фибоначчи и золотая спираль позиционируются как универсальный закон мироздания, с помощью которого можно описать любой природный процесс или объекты, от расположения лепестков цветка до формы спиральных галактик. Хотя в отношении многих природных явлений это действительно так, принцип не является всеобъемлющим: например, те же рукава спиральных галактик или раковина моллюска наутилуса закручены по логарифмической спирали, которая, хоть и близка по форме к золотой, все же ей не является.
• Идеальность. Распространено мнение, что золотое сечение и спираль Фибоначчи описывают идеальные пропорции. Однако исследования показали, что объекты, построенные по этому принципу (например человеческое тело), при демонстрации обычным людям воспринимаются обычно как диспропорциональные, вытянутые. Отсюда является заблуждением и утверждение, что все великие художники эпохи Возрождения и последующих времен использовали принцип золотой спирали в своих работах. Такие эксперименты действительно случались, но это не было распространенным явлением.
• Практическая применимость. Еще один миф говорит о том, что использование золотого сечения и чисел Фибоначчи в любом сфере деятельности дает положительный результат. Но, например, криптографы знают, что метод Фибоначчи с запозданием не является идеальным способом усилить шифрование — многие генераторы случайных чисел на его основе либо медленно работают, либо имеют недостаточный порог устойчивости к взлому. А использование принципов золотого сечения в архитектуре или промышленном дизайне редко сочетается с оптимизацией производства.

Вместе с тем нельзя отрицать большую роль фибоначчиевых чисел в развитии фундаментальной и прикладной математики, информатики и смежных с ними наук. Разработанные на основе золотой спирали методы и технологии широко применяются в разных областях человеческой жизни, от сугубо научных до прикладных, таких как компьютерная графика, криптография, программирование, обработка данных и т.д.

Выберите IT-профессию, которая вам нравится, а мы поможем научиться: