Дискретная математика изучает структуры, которые состоят из конечного или счетного числа элементов, таких как целые числа, графы, логика и множества. Главное свойство таких объектов — дискретность, то есть их разделимость на отдельные неделимые части. Это отличает дискретную математику от математического анализа и физики, где работают с непрерывными величинами, такими как функции и пределы.
В статье разбираем основные понятия, а еще рассказываем, как дискретную математику используют в IT.
Множества
Множество — это совокупность элементов, которыми могут быть числа, объекты, символы и другие объекты. Важные свойства множества: порядок элементов не имеет значения, а одинаковые элементы не повторяются.
Есть несколько видов множеств:
- Конечное множество. Множество, включающее конечное количество элементов.
Пример: A = {1, 2, 3}.
- Бесконечное множество. Множество с бесконечным числом элементов.
Пример: B= {1, 2, 3, …} (множество всех натуральных чисел).
- Подмножество. Множество, элементы которого включены в другое множество.
Пример: A = {1, 2}, B = {1, 2, 3}, A⊆B.
- Тождественное множество. Множество, включающее все элементы некоторой универсальной области.
Пример: U = {1, 2, 3, 4}.
- Пустое множество. Множество, не содержащее ни одного элемента. Обозначается как ∅ (символ пустого множества).
Разберем основные операции со множествами:
- Объединение (A ∪ B) — множество всех элементов, которые принадлежат хотя бы одному из множеств A или B.
Пример: A = {1, 2}, B = {2, 3}, A ∪ B = {1, 2, 3}.
- Пересечение (A ∩ B) — множество всех элементов, которые одновременно принадлежат A и B.
Пример: A = {1, 2}, B = {2, 3}, A ∩ B = {2}.
- Разность (A − B) — множество всех элементов, которые принадлежат A, но не принадлежат B.
Пример: A = {1, 2, 3}, B = {2, 4}, A − B = {1, 3}.
- Симметрическая разность (A △ B) — множество всех элементов, которые принадлежат либо A, либо B, но не одновременно.
Пример: A = {1, 2}, B = {2, 3}, A △ B = {1, 3}.
- Дополнение (A′) — множество всех элементов области U, которые не принадлежат A.
Пример: если U = {1, 2, 3, 4}, A = {1, 2}, то A′ = {3, 4}.
Работая с множествами, часто нужно проверять истинность определенных утверждений, например: «Элемент принадлежит множеству или нет?» Это приводит нас к логике — науке, которая изучает истинность высказываний и их комбинации.
Логика: булевы операции, истинность высказываний
Логика изучает высказывания — предложения, которые могут быть истинными (1 или True) или ложными (0 или False).
Чтобы работать с такими высказываниями, используют специальные правила — булевы операции. Они определяют, как сочетать высказывания и проверять, истинно ли сложное утверждение.
Рассмотрим основные булевы операции и их правила.
Отрицание (NOT)
Изменяет логическое значение высказывания на противоположное.
| A | NOT A |
| 1 | 0 |
| 0 | 1 |
Пример:
Если A = 1 («Идет дождь»), то NOT A = 0 («Дождя нет»).
Конъюнкция (AND)
Операция «и» возвращает истину (1), только если оба высказывания истинны.
| A | B | A AND B |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Пример:
Если A = 1 («Идет дождь»), а B = 1 («Я взял зонт»), то A AND B = 1 («Идет дождь, и я взял зонт»).
Дизъюнкция (OR)
Операция «ИЛИ» возвращает истину, если хотя бы одно из высказываний истинно.
| A | B | A OR B |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Пример:
Если A = 0 («Дождя нет»), B = 1 («На улице холодно»), то A OR B = 1 («Или на улице идет дождь, или холодно»).
Исключающее «ИЛИ» (XOR)
Истинно, если только одно из высказываний истинно.
Таблица истинности
| A | B | A XOR B |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Примеры:
- Если A = 1 («Идет дождь»), а B = 0 («На улице не холодно»), то A XOR B = 1 («Идет дождь, но на улице не холодно»).
- Если A = 1 («Идет дождь»), а B = 1 («На улице холодно»), то A XOR B = 0 («Идет дождь и на улице холодно одновременно» — операция «ИЛИ» не выполняется).
Импликация (IF A THEN B)
Ложна только в случае, когда A = 1, а B = 0.
Логическое следование обозначается стрелкой →.
| A | B | IF A THEN B |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Пример:
Если A = 1 («Идет дождь»), а B = 0 («Я не взял зонт»), то A → B = 0 («Если идет дождь, то я должен был взять зонт, но этого не произошло» — утверждение ложно).
Теперь, когда мы знаем, как анализировать высказывания, можно описывать связи между элементами разных множеств. Это называется отношениями.
Отношения
Отношение — это связь между элементами двух (или одного) множеств. Например, отношение R на множествах A и B обозначается как R ⊆ A × B, где A × B — декартово произведение всех возможных пар (a, b), где a ∈ A, b ∈ B.
Виды отношений
- Рефлексивное. Каждый элемент связан с самим собой.
R рефлексивно, если ∀a ∈ A, (a, a) ∈ R.
Пример: A = {1, 2}, R = {(1, 1), (2, 2)}.
- Симметричное. Если aRb, то bRa.
Пример: A = {1, 2}, R = {(1, 2), (2, 1)}.
- Антисимметричное. Если aRb и bRa, то a = b.
Пример: A = {1, 2}, R = {(1, 1), (2, 2), (1, 2)}.
- Транзитивное. Если aRb и bRc, то aRc.
Пример: A = {1, 2, 3}, R= {(1, 2), (2, 3), (1, 3)}.
Один из особых видов отношений — это функции. Разберем их подробнее в следующем разделе.
Функции
Функция — это частный случай отношения, где каждому элементу множества A (область определения) сопоставляется только один элемент множества B (область значений).
Обозначается f : A → B.
Свойства функции:
- Инъекция (взаимно-однозначное отображение).
Разным элементам множества A соответствуют разные элементы множества B.
Пример: f(x) = x + 1, A = {1, 2}, B = {2, 3}.
- Сюръекция.
Все элементы множества B имеют соответствие в A. Иными словами, сюръекция — это функция, которая «покрывает» все множество B.
Пример: f(x) = x2, A = {−2, −1, 1, 2}, B = {1, 4}.
- Биекция.
Функция одновременно инъективна и сюръективна.
Пример: f(x) = x + 1, A = {1, 2}, B = {2, 3}.
Основные типы функций:
- Арифметическая функция: f(x) = x + 2.
- Булева функция: f(x, y) = x ∧ y (логическое «И»).
- Показательная: f(x) = 2x.
При работе с функциями и множествами часто возникает вопрос: сколько всего существует способов распределить элементы множества? Этим занимается комбинаторика.
Комбинаторика
Комбинаторика — это раздел математики, который помогает ответить на вопрос о том, сколько разных групп (комбинаций) можно составить из множества объектов.
Разберем задачи комбинаторики.
Перестановки
Перестановка — это упорядоченная последовательность всех элементов множества.
Формула:
\[ P_n = n! \]
где n! — факториал.
Пример:
Для множества {1, 2, 3} возможные перестановки: {123, 132, 213, 231, 312, 321}.
Если перестановки берутся не для всех элементов, а только для k, используется формула:
\[ P_n^k = \frac{n!}{(n-k)!} \]
где:
- n! — количество всех перестановок n элементов;
- (n − k)! — это факториал «оставшихся» n − k элементов, которые мы не выбираем.
Второй пример:
Для множества {A, B, C} выбираем 2 элемента для составления пары-размещения: AB, BA, AC, CA, BC, CB. Всего P32=6.
Сочетания
Сочетание — это способ выбора k-элементов из множества n, где порядок не важен.
Формула:
\[ C_n^k = \frac{n!}{k!(n-k)!} \]
Пример:
Для множества {A, B, C} выбираем 2 элемента для составления пары-сочетания: AB, AC, BC.
Всего \( C_3^2 = 3 \).
Комбинаторика тесно связана с числами, например при подсчете делителей или решении задач с остатками. Чтобы лучше понимать такие задачи, нужно изучить свойства чисел — этим занимается теория чисел.
Теория чисел
Теория чисел — это раздел математики, который изучает свойства и взаимосвязи целых чисел. Она включает множество понятий, которые находят применение в криптографии, алгоритмах и комбинаторике. Рассмотрим основные элементы теории чисел.
Делимость и простые числа
Делимость позволяет определить, делится ли одно число на другое без остатка. Например, 15 делится на 3, но не делится на 4.
Простые числа — это числа больше 1, которые делятся только на 1 и на себя. Например: 2, 3, 5, 7, 11. Простые числа важны, потому что любое целое число можно разложить на произведение простых множителей:
12 = 2 × 2× 3
Алгоритм Евклида
Для нахождения наибольшего общего делителя (НОД) двух чисел используется алгоритм Евклида. Он основан на последовательном делении с нахождением остатка.
Пример: найдем НОД для 36 и 48:
- 48 делится на 36 с остатком 12.
- Теперь ищем НОД для 36 и 12. Остаток 0.
- Значит, НОД = 12.
Этот алгоритм широко применяется в задачах криптографии и анализа данных.
Взаимно простые числа
Взаимно простыми называются числа, у которых НОД равен 1. Например, 15 и 28 — взаимно простые.
Это свойство важно в модулярной арифметике, где часто требуется их учитывать.
Модулярная арифметика
Изучает остатки от деления чисел.
Например: 7 mod 3 = 1,поскольку при делении 7 на 3 остаток равен 1.
Эти свойства широко применяются в криптографии (например, в RSA) и в алгоритмах, работающих с периодическими данными.
Теоремы о числах
- Малая теорема Ферма.
Если p — простое число, а а не делится на p, то:
\[ a^{p-1} = 1 \, (\text{mod} \, p) \]
Это ключевой инструмент для проверки простоты чисел и работы криптографических алгоритмов.
- Последняя теорема Ферма.
Доказывает, что для n > 2n нет целых чисел x, y, z, удовлетворяющих уравнению:
\[ x^n + y^n = z^n \]
- Теорема о распределении простых чисел.
Описывает закономерности в расположении простых чисел среди всех целых чисел. Например, простые числа встречаются реже по мере увеличения чисел, но их общее количество бесконечно.
После изучения чисел логично перейти к теории графов, которая описывает более сложные структуры, такие как сети, схемы или пути, где связи между элементами можно представить наглядно.
Теория графов
Граф — это математическая структура, состоящая из множества вершин и ребер, соединяющих эти вершины.
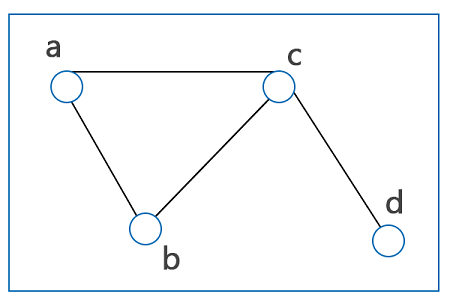
Графы используют для моделирования множества реальных ситуаций, например сетевых соединений, маршрутов, отношений между объектами.
Типы графов по свойствам
Графы можно классифицировать по различным свойствам. Одни из ключевых — связность и наличие циклов.
Связные и несвязные графы
- Связный граф — граф, в котором для каждой пары вершин существует путь.
- Несвязный граф — граф, у которого существует хотя бы одна пара вершин, между которыми нет пути.
Циклические и ациклические графы
- Циклический граф — граф, который содержит хотя бы один цикл, т. е. путь, который начинается и заканчивается в одной и той же вершине.
- Ациклический граф не содержит циклов.
Типы графов по структуре
Ориентированные графы (Digraphs)
В ориентированном графе ребра имеют направление, то есть соединяют вершины в определенном порядке.
Пример:
Маршруты общественного транспорта: вершины — остановки, а ребра показывают направление движения автобусов или поездов.

Неориентированные графы
В неориентированном графе ребра не имеют направления, то есть связь между вершинами симметрична.
Пример:
Граф дружбы в социальной сети: вершины — пользователи, а ребра показывают, что два человека являются друзьями. Если А и В друзья, это всегда взаимно.
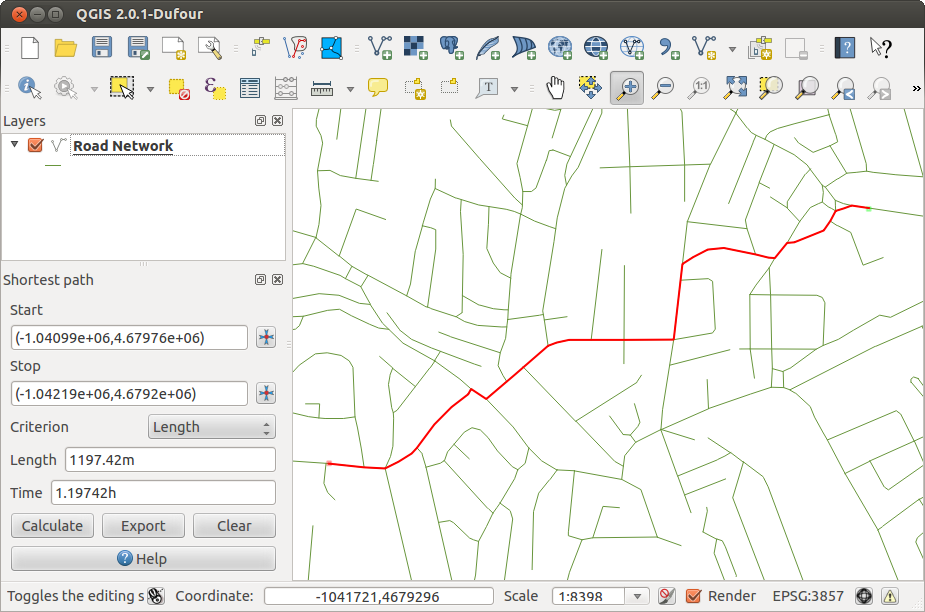
Взвешенные графы
В графах с весами каждому ребру присваивается некоторое значение (вес), например расстояние, стоимость или время.
Пример:
Граф маршрутов, где ребра представляют время в пути или стоимость поездки.
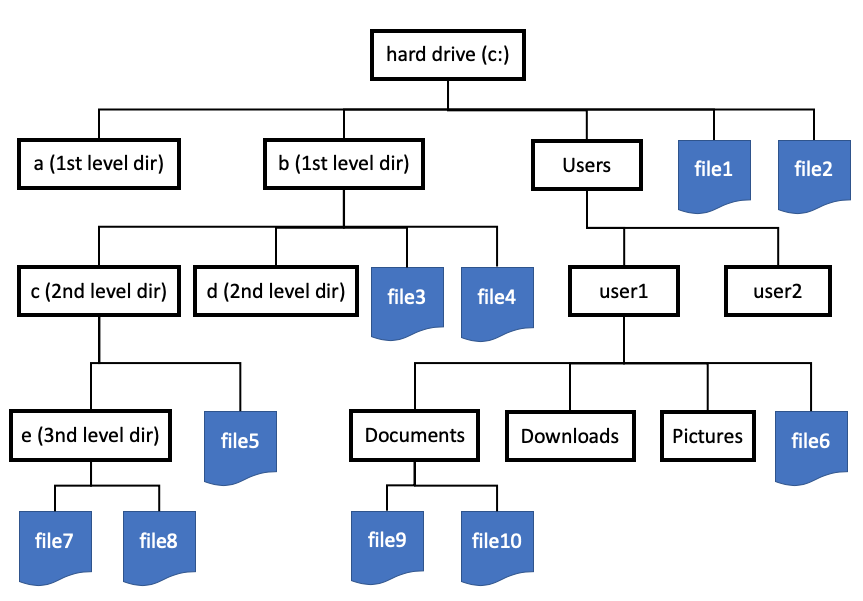
Деревья
Дерево — это связный ациклический граф. В дереве существует только один путь между любой парой вершин.
Пример:
Структура каталогов на компьютере.
Двудольные графы
Графы, чьи вершины можно разделить на две группы так, что ребра соединяют только вершины из разных групп.
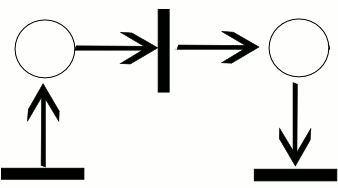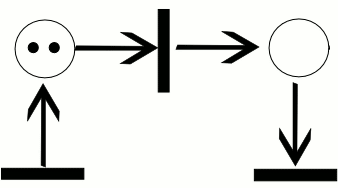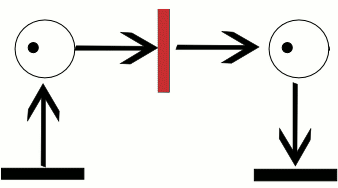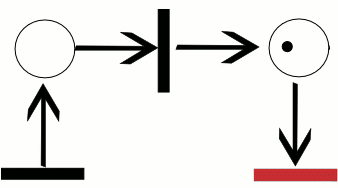
Пример:
Сети Петри, которые нужны для моделирования динамических дискретных систем.
Графы тесно связаны с алгоритмами, которые помогают находить пути, упрощать сети и анализировать большие структуры. Алгоритмы — это практическая реализация знаний дискретной математики. Разберем их детально.
Алгоритмы
Это последовательность четко определенных шагов или инструкций для решения задачи или достижения определенной цели. Один из ключевых параметров алгоритмов — алгоритмическая сложность (алгосложность), которая показывает, как растет количество операций в зависимости от объема данных.
Принципы дискретной математики лежат в основе многих алгоритмов. Рассмотрим несколько их категорий.
Алгоритмы поиска
Применяются для нахождения нужных данных в коллекциях. Они различаются по сложности и эффективности.
- Линейный поиск.
Последовательное сравнение каждого элемента с искомым. Используется для небольших и неотсортированных данных.
Алгосложность: O (n), где n — количество элементов.
- Двоичный поиск.
Применяют к отсортированным данным. На каждом шаге массив делится пополам, и поиск продолжается в одной из частей.
Алгосложность: O (log n).
- Поиск в графах.
Алгоритмы поиска в глубину (DFS) и поиска в ширину (BFS) используют для обхода графов и поиска вершин, которые связаны друг с другом. Можно применять для маршрутизации в сетях или поиска пути в навигации.
Алгосложность: O (V + E), где V — количество вершин в графе, E — количество ребер в графе.
Используются для упорядочивания данных. Их эффективность зависит от структуры данных и выбранного метода.
- Пузырьковая сортировка.
Один из самых простых методов. Элементы массива последовательно сравниваются и «перемещаются» на нужные места.
Алгосложность: O (n2).
- Быстрая сортировка (Quick Sort).
Тут работает принцип «разделяй и властвуй»: массив делится на подмассивы, которые сортируются рекурсивно.
Алгосложность: O (n log n).
- Сортировка слиянием (Merge Sort).
Использует рекурсию для разделения массива на части, а затем слияние отсортированных подмассивов.
Алгосложность: O (n log n).
Применяется для больших объемов данных, где стабильность важнее скорости.
Теория вероятностей и статистика
Дискретная математика тесно связана с теорией вероятностей, особенно при работе с событиями, которые имеют конечное или счетное множество исходов. Эти события называются дискретными, и их вероятности вычисляются с использованием методов, таких как комбинаторика.
Основы вероятности
Вероятность события
Выражается значением от 0 до 1, где 0 означает невозможность события, а 1 — его неизбежность.
Если эксперимент может привести к n исходам, из которых k — благоприятные, то вероятность события P (E) вычисляется как:
\[ P(E) = \frac{k}{n} \]
Пример:
При подбрасывании монеты вероятность выпадения орла равна
\[ P(\text{Орел}) = \frac{1}{2} \]
Закон больших чисел
Утверждает, что с увеличением числа испытаний частота наступления события стремится к его теоретической вероятности.
Теорема о полной вероятности
Если пространство вероятностей можно разделить на несколько взаимно исключающих событий, то вероятность события можно выразить через их вероятности.
Условная вероятность
Вероятность наступления события A, если известно, что событие B уже произошло:
\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \]
События
- Независимые события. Два события называются независимыми, если вероятность их совместного наступления равна произведению их вероятностей.
\[ P(A \cap B) = P(A) \cdot P(B) \]
- Зависимые события. Если события зависят друг от друга, вероятность их совместного наступления не равна произведению их индивидуальных вероятностей.
Распределения вероятности
- Дискретное распределение. События имеют конечное или счетное множество исходов.
Например, при броске игральной кости вероятность каждого числа равна 16.
- Непрерывное распределение. Исходы принимают значения из некоторого интервала.
Например, нормальное распределение описывает вероятности для случайных величин, таких как рост или вес людей.
Как теория вероятностей связана со статистикой?
Теория вероятностей создает математические законы для оценки вероятности событий, а статистика использует эти законы для анализа данных, тестирования гипотез и прогнозирования.
- Теория вероятностей отвечает на вопрос «Какова вероятность события при заданных условиях?».
- Статистика помогает ответить: «Что можно сказать о реальных данных, основываясь на вероятностных законах?»
Если бросить шестигранный кубик, вероятность выпадения числа 3 равна 16 (около 16,7%). Статистика помогает проверить, совпадает ли эта вероятность с реальностью. Например, если из 60 бросков число 3 выпало 8 раз, она покажет, связано ли это с погрешностью или с тем, что кубик нечестный.
Как дискретная математика используется в IT
Дискретная математика лежит в основе многих технологий, инструментов и решений, используемых в IT. Все ее разделы — от теории множеств до алгоритмов — находят практическое применение. Рассмотрим основные направления, где она играет ключевую роль.
Алгоритмы и структуры данных
Это фундамент программирования, их разработка напрямую связана с дискретной математикой.
- Графы. Используются для моделирования и поиска путей в сетях, таких как маршрутизация в интернете, прокладка кабельных сетей или навигация.
Пример: алгоритм Дейкстры ищет кратчайший путь в графе, например, для навигации в Google Maps.
- Деревья. Служат для эффективного поиска и сортировки данных.
Пример: двоичное дерево поиска (Binary Search Tree) используется в базах данных или файловых системах.
- Хэш-таблицы. Это структура данных, основанная на принципах дискретной математики, которая обеспечивает быструю индексацию и доступ к данным.
Пример: используются в больших массивах данных, таких как клиентская база, где нужно быстро находить записи по уникальному идентификатору.
Оптимизация
Комбинаторика и связанные с ней методы помогают находить оптимальные решения сложных задач. Например, распределять вычислительные мощности в облаках и ускорять обработку запросов.
Криптография
Криптография использует теорию чисел и алгоритмы шифрования для защиты данных. Алгоритм RSA применяет свойства простых чисел. Его используют в протоколах безопасности, таких как HTTPS.
Код
Математическая логика играет важную роль в написании корректного и надежного кода, а также в его проверке и оптимизации.
- Оптимизация программ. Логические операции делают вычисления проще и ускоряют выполнение задач.
Пример: булева логика используется в процессорах для повышения эффективности обработки данных.
- Тестирование кода. Логические выражения применяют для проверки работоспособности программ.
Пример: в тестах можно задать условие: «Если введен неверный пароль, программа должна вывести сообщение об ошибке».
Базы данных
Множества и отношения, изучаемые в дискретной математике, лежат в основе реляционных баз данных.
Пример: в SQL таблицы представляют множества, а операции над ними, такие как объединение, пересечение и разность, соответствуют математическим действиям с множествами.
Анализ данных и машинное обучение
Теория вероятностей и статистика применяют в IT для анализа данных, прогнозирования и работы с неопределенностью. Рассмотрим основные направления.
Прогнозирование
Вероятностные методы помогают предсказывать будущие показатели на основе данных из прошлых периодов.
Примеры:
- Интернет-магазины анализируют предыдущие продажи, чтобы прогнозировать спрос на товары.
- Погодные сервисы рассчитывают вероятность дождя, используя исторические данные.
Анализ данных
Статистические методы помогают выявлять закономерности, оценивать значимость результатов и улучшать принятие решений.
Пример: в A/B-тестировании статистика показывает, насколько изменения на сайте влияют на конверсию.
Принятие решений
Алгоритмы используют вероятности для выбора оптимального варианта из нескольких.
Пример: рекомендательные системы определяют, какие фильмы или товары понравятся пользователю, и предлагают их в приоритетном порядке.
Анализ неопределенности
Теория вероятностей используется для оценки вероятности случайных событий и их влияния.
Пример: в сетевых системах рассчитывается вероятность потери данных, чтобы выбрать более надежный маршрут передачи.
Оценка рисков
Вероятностные методы помогают анализировать возможные риски и минимизировать их последствия.
Пример: в кибербезопасности рассчитывают вероятность различных атак, чтобы заранее принять меры и усилить защиту.
Машинное обучение
Вероятностные модели и статистика лежат в основе обучения алгоритмов.
Примеры:
- Наивный байесовский классификатор анализирует вероятность принадлежности письма к спаму.
- Регрессионные модели предсказывают стоимость недвижимости.







