Парадокс Монти Холла: что общего у машинного обучения и игры в двадцать одно

Фундамент, на котором стоит весь Machine Learning (ML) и Data Science, — это теория вероятностей. Сегодня обратимся к одной из ее важных составляющих — парадоксу Монти Холла. На его примере мы разберем, как легко наш мозг попадает в ловушки когнитивных искажений и почему интуиция — не лучший помощник в анализе данных.

«Бен, вы участвуете в телеигре…»

В начале фильма «Двадцать одно» (2008 г.) есть блестящая сцена. Профессор Микки Роса (Кевин Спейси) задает студенту Бену Кэмпбеллу задачку. Бен оказывается в гипотетической телеигре, где перед ним три двери. За одной — новенький красный автомобиль, за двумя другими — козы (в фильме их заменили на «самокаты», но суть та же).

Бен выбирает дверь №1. Ведущий, который знает, что находится за дверями, открывает дверь №3, и там оказывается коза. После этого ведущий спрашивает Бена: «Вы хотите изменить свой выбор и открыть дверь №2 или останетесь при своем?»

Большинство студентов в аудитории (как и большинство людей в жизни) сказали бы: «Нет смысла менять, шансы 50 на 50». Но Бен отвечает иначе: «Да, я меняю выбор. Изначально шанс был 33,3%, но теперь, если я сменю дверь, вероятность победы вырастет до 66,7%».

Профессор в восторге: «Помните о замене переменной!» Бен получает «отлично» и приглашение в закрытый клуб игроков в блэк-джек, потому что умеет контролировать свои эмоции и мыслить логически.

Но почему так происходит? Почему интуитивное «две двери — значит 50/50» не работает? И, что еще важнее для нас, специалистов по данным: почему условия, при которых генерируются данные (поведение ведущего), важнее самих данных?

Давайте разбираться.

Постановка парадокса Монти Холла и математическое решение

Парадокс назван в честь Монти Холла — многолетнего ведущего американского шоу Let’s Make a Deal. В классической постановке задачи условия жестко фиксированы, и это критически важно для расчета вероятностей.

Условия задачи (классика):

1. Есть три двери. За одной — приз (авто), за двумя — пустышки (козы).
2. Вы выбираете одну дверь (пусть это будет дверь А).
3. Ведущий (Монти) знает, где находится автомобиль.
4. Монти обязан открыть одну из оставшихся дверей.
5. Монти никогда не открывает дверь с автомобилем.
6. Монти никогда не открывает дверь, которую выбрали вы.
7. Монти предлагает вам сменить выбор на оставшуюся закрытую дверь.

Вопрос: стоит ли менять выбор?

Интуитивная ошибка (ловушка равновероятности)

Наш мозг работает эвристиками. Он видит: осталась дверь А (наша) и дверь Б (чужая). Одна пустая, одна с машиной. Значит, вероятность 1/2. Это ошибка, потому что мы игнорируем априорную вероятность и условную информацию, которую нам дал ведущий. Он не просто открыл случайную дверь, а действовал по алгоритму, который внес энтропию в систему.

Решение через пространство событий

Давайте представим все возможные исходы. Допустим, вы всегда выбираете дверь 1.

Сценарий	Где машина?	Ваш выбор	Действие Монти (открывает козу)	Если вы ОСТАЕТЕСЬ	Если вы МЕНЯЕТЕ
№1	Дверь 1	Дверь 1	Монти открывает Дверь 2 или 3	ПОБЕДА	ПРОИГРЫШ
№2	Дверь 2	Дверь 1	Монти обязан открыть Дверь 3	ПРОИГРЫШ	ПОБЕДА
№3	Дверь 3	Дверь 1	Монти обязан открыть Дверь 2	ПРОИГРЫШ	ПОБЕДА

Анализ таблицы:

• Если вы не меняете выбор, вы выигрываете только в сценарии №1. Вероятность этого сценария — 1/3.
• Если вы меняете выбор, вы выигрываете в сценариях №2 и №3. Суммарная вероятность — 2/3.

Вывод: смена двери удваивает ваши шансы на победу.

Визуализация процесса (D2 Diagram)

Для тех, кто лучше воспринимает графы (как мы, ML-инженеры, когда смотрим на Decision Trees), нарисуем схему принятия решений.

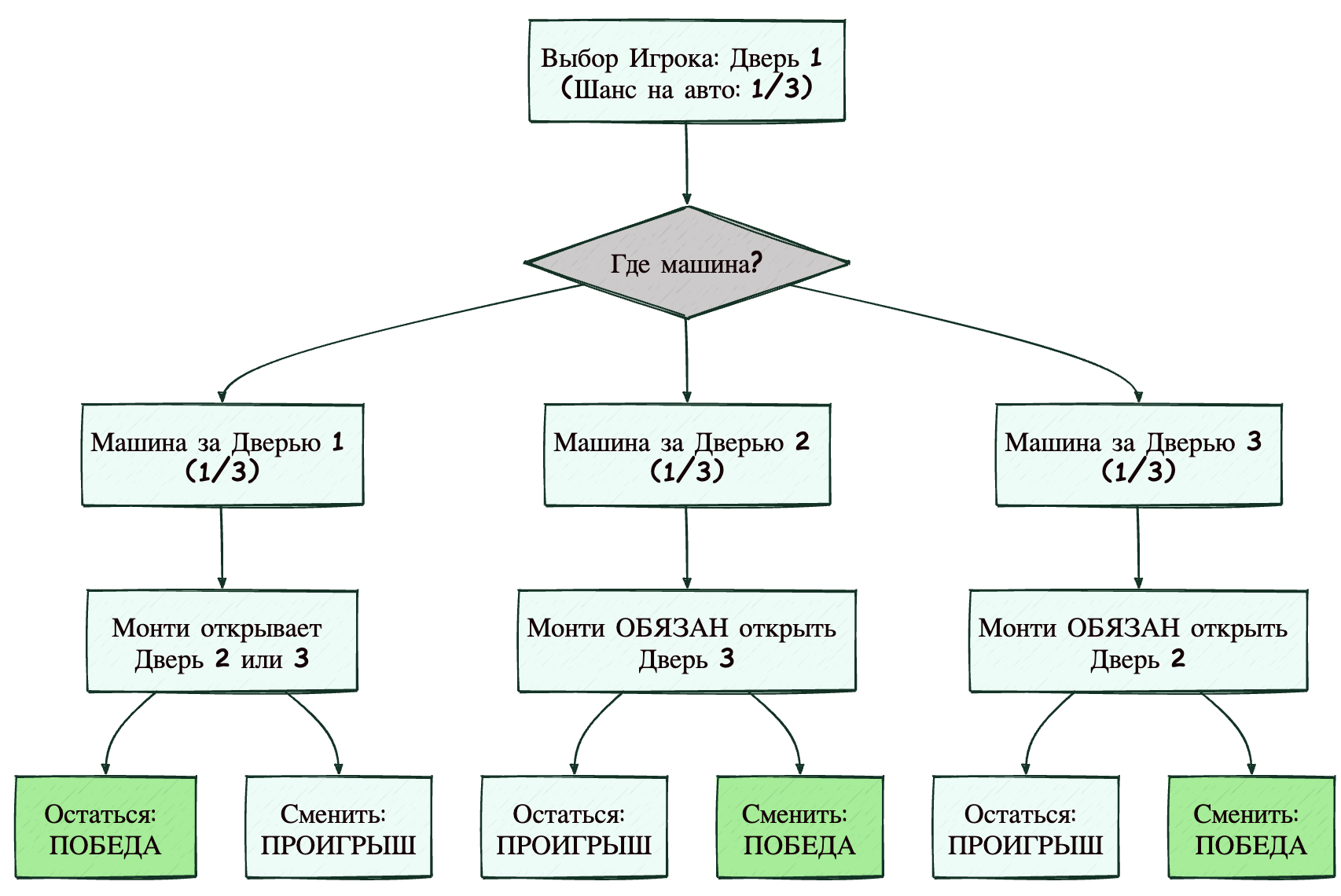
На диаграмме четко видно: ветки, ведущие к победе при смене выбора, покрывают два из трех возможных начальных состояний мира.

Взгляд через теорему Байеса (для любителей формул)

В ML мы постоянно используем байесовский вывод. Давайте применим его здесь. Пусть H1,H2,H3 — гипотезы, что машина за дверью 1, 2 или 3. P(H_i)=1/3. Пусть D — событие: Монти открыл дверь 3. Мы выбрали дверь 1. Нам нужно найти вероятность P(H₂|D) — вероятность того, что машина за дверью 2, при условии, что Монти открыл дверь 3.

По формуле Байеса:

Разберем компоненты:

1. P(H₂)=1/3 (априорная вероятность).
2. P(D|H₂) (вероятность того, что Монти откроет дверь 3, если машина за дверью 2). Если машина за дверью 2, а мы выбрали дверь 1, у Монти нет выбора — он обязан открыть дверь 3. Значит, вероятность равна 1.
3. P(D) (полная вероятность того, что Монти откроет дверь 3).

• Если машина за дверью 1: Монти открывает 2 или 3 с вероятностью 1/2. Вклад: 1/31/2=1/6.
• Если машина за дверью 2: Монти открывает 3 с вероятностью 1. Вклад: 1/31=1/3.
• Если машина за дверью 3: Монти открывает 2. Вероятность открыть 3 равна 0.
• Итого P(D)=1/6+1/3+0=1/2.

Считаем:

Вуаля! Вероятность того, что машина за второй дверью, — 66,7%. Математика не врет.

А что, если ведущий ведет себя иначе? (Неклассические версии)

В Data Science есть золотое правило: «Garbage in, Garbage out» («Мусор на входе — мусор на выходе»). Но есть и другое, менее очевидное: важно понимать процесс генерации данных.

Если мы изменим алгоритм поведения Монти (процесс генерации события «открытая дверь»), вероятности могут кардинально измениться. Это важно, чтобы понять, почему в ML нельзя бездумно применять модели.

Вариант А: «Монти-невежда» (Ignorant Monty)

Представьте, что ведущий забыл, где машина. Он просто наугад открывает одну из оставшихся дверей.

• Вы выбрали дверь 1.
• Монти наугад открывает дверь 3.
• О чудо! Там коза (машины нет).

Стоит ли менять выбор? В этом случае — нет разницы. Вероятности становятся 50/50.

Почему? Потому что в сценарии, где машина была за дверью 3, «Монти-невежда» открыл бы ее и игра бы закончилась (вы увидели машину и проиграли бы сразу, так как не выбрали ее). Тот факт, что мы видим закрытые двери и открытую козу, означает, что мы отфильтровали часть выборки. В классической версии Монти избегает открытия машины, тем самым передавая нам информацию. Здесь же он просто случайно не попал в нее.

Пример из Machine Learning: это похоже на ошибку выжившего. Если вы обучаете модель кредитного скоринга только на тех, кому уже выдали кредит (и игнорируете тех, кому отказали), ваша модель будет вести себя как игрок против «Монти-невежды». Она не видит полной картины мира.

Вариант Б: «Ленивый Монти»

Ведущий знает, где машина, но ему лень тянуться. Если вы выбрали дверь 1, а машина за дверью 1, он всегда открывает дверь 3 (потому что она ближе к его выходу со сцены, например) и никогда не открывает дверь 2, если у него есть выбор. Если в такой ситуации Монти открыл дверь 3 — стоит ли менять выбор? Вероятность того, что машина за дверью 2, становится еще выше, чем 2/3! А если он открыл дверь 2 — то машина гарантированно за дверью 1 (потому что если бы она была за дверью 3, он бы открыл дверь 2, но если бы она была за дверью 1, он бы открыл «любимую» дверь 3).

Это пример смещенных данных (Bias). Если вы знаете о привычках «генератора данных» (Монти), вы можете извлечь еще больше информации.

Задача трех узников: тот же скелет, но в другом обличии

В математике есть понятие изоморфизма — когда две задачи выглядят по-разному, но структурно идентичны. У парадокса Монти Холла есть «брат-близнец», задача трех узников. Она часто взрывает мозг даже тем, кто понял Монти Холла.

Постановка задачи

В тюрьме сидят трое заключенных: Алан, Билл и Чарли. Начальник тюрьмы объявляет: «Завтра двоих из вас казнят, а одного помилуют. Я уже знаю, кто помилован, но не скажу». Узник Алан умоляет охранника: «Послушай, я знаю, что кого-то из моих друзей (Билла или Чарли) точно казнят. Назови мне имя того, кого точно казнят. Это ведь не даст мне информации о моей судьбе, ведь я и так знаю, что один из них умрет». Охранник соглашается и говорит: «Билла точно казнят».

Алан радуется: «Фух! Раньше шанс моего помилования был 1/3. Теперь нас осталось двое — я и Чарли. Значит, мои шансы выросли до 1/2 (50%)!»

Прав ли Алан?

Решение

Нет, Алан не прав. Его ситуация абсолютно идентична игроку в шоу Монти Холла, который выбрал первую дверь и не меняет выбор.

• Приз (помилование) — это автомобиль.
• Узники — это двери.
• Охранник — это Монти Холл.
• Фраза «Билла казнят» — это открытие двери с козой.

Когда охранник говорит, что Билла казнят, он (как и Монти) не мог назвать Алана (по условию он не говорит узнику о его судьбе).

1. Если помилован Алан (1/3): Охранник мог назвать Билла или Чарли (с вероятностью 50%).
2. Если помилован Билл (1/3): Охранник обязан назвать Чарли. (Но этот сценарий отпадает, так как назван Билл).
3. Если помилован Чарли (1/3): Охранник обязан назвать Билла.

Поскольку охранник назвал Билла, мы находимся либо в сценарии 1 (где вероятность была размыта пополам), либо в сценарии 3 (где вероятность полная). Вероятность того, что помилован Чарли, теперь составляет 2/3. Алан остался при своих 1/3.

Почему это важно для ML? 

Представьте, что вы строите модель диагностики заболеваний.

• Пациент А (Алан).
• Болезни Б и Ч (Билл и Чарли).
• Тест исключает Болезнь Б.

Значит ли это, что вероятность здоровья пациента и вероятность Болезни Ч стали равны? Нет! Если Болезнь Ч встречается в популяции гораздо чаще или если тест специфичен определенным образом, вероятности перераспределяются нелинейно. Игнорирование этого ведет к неверным диагнозам.

Парадокс Монти Холла: коротко о главном

Итак, что мы узнали, разобрав этот классический парадокс?

1. Интуиция плоха в условных вероятностях. Наш мозг эволюционно заточен на простые линейные связи. Когда появляется новая информация, меняющая условия задачи (ведущий открыл дверь), мы часто забываем пересчитать вероятности с нуля.
2. Контекст важнее факта. Само по себе открытие двери с козой не несет информации. Информацию несет то, почему и как ведущий открыл именно эту дверь. В Data Science это значит: всегда задавайте вопрос «Как были собраны эти данные?». Есть ли там систематическая ошибка выжившего? Есть ли скрытые правила фильтрации?
3. Всегда меняйте дверь. Ну, по крайней мере, в классической задаче Монти Холла. В жизни и в ML это метафора гибкости: будьте готовы обновить свои прогнозы (Priors), когда поступают новые данные (Likelihood), чтобы получить корректный апостериорный вывод (Posterior).

Как сказал бы Бен Кэмпбелл из фильма «21»: «Я благодарен за лишние проценты». В мире больших данных и высокой конкуренции разница между 33% и 67% — это разница между провалом и колоссальным успехом.

Изучайте теорию вероятностей, друзья, — это та магия, которая заставляет ваши нейросети работать!