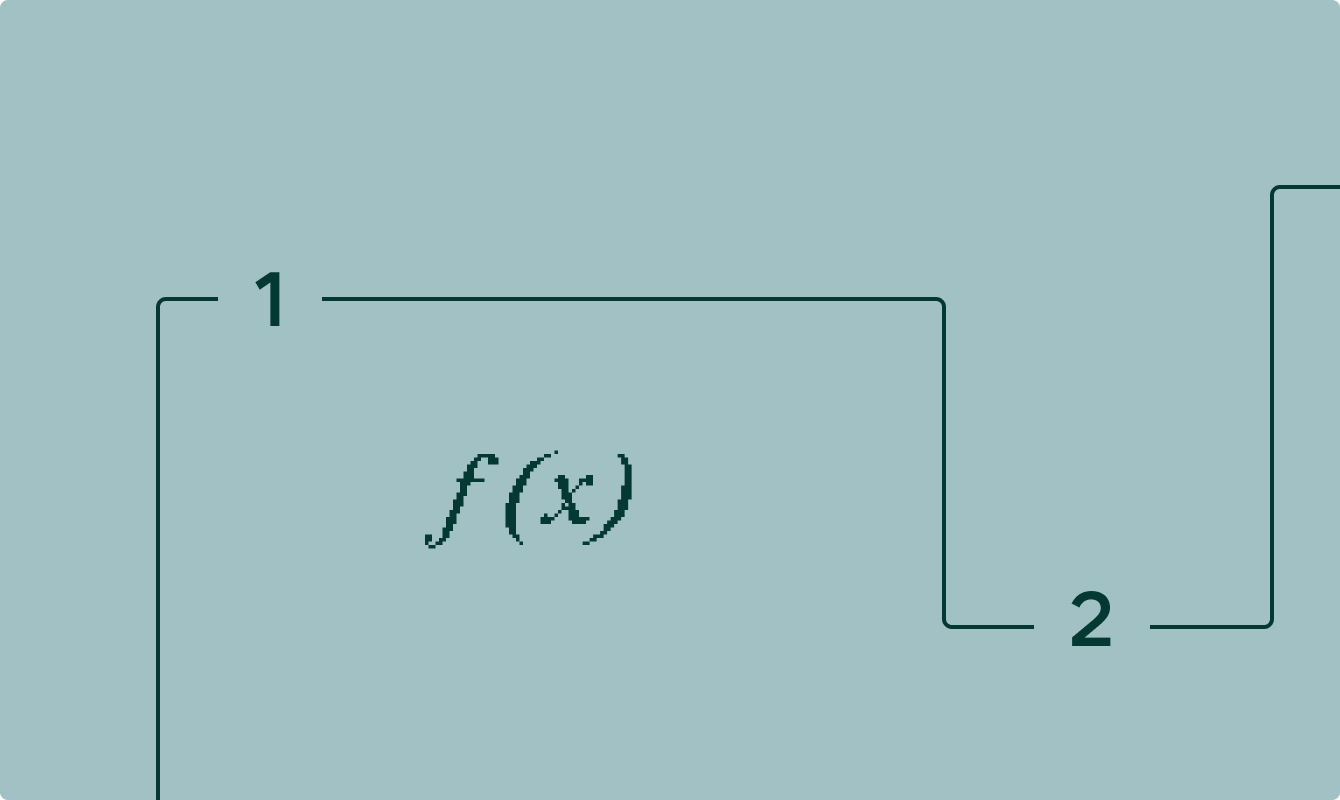Что такое предел функции в математике

Показываем на примерах, как рассчитать предел функции

5 ноября 2024

Скопировано

Содержание

Предел функции — одно из ключевых понятий в математическом анализе, которое описывает, к какому значению приближается функция, когда ее аргумент, то есть входное значение, стремится к определенной точке или бесконечности. Разберем, зачем рассчитывать предел функции и где применять результаты.

Как выглядит формула предела и что она означает

В математике пределы применяют в определении непрерывности и вычислении производных функции, а в физике — для моделирования процессов, таких как движение объектов, где важны малейшие изменения величин. При этом, формулы и определение предела в физике и математике одинаковы.

Предел функции f(x) при x, стремящемуся к значению a, записывается как:

\[ \lim\limits_{x \to a} f(x) = L \]

lim — символ, обозначающий «предел»;
x→a — означает, что переменная x стремится к значению a. То есть мы рассматриваем, что происходит с функцией, когда значение x приближается к значению a;
f(x) — функция, значение которой мы исследуем;
L — конкретное значение, к которому приближается значение функции f(x) по мере того, как x стремится к a.

Это означает, что при приближении x к a значение функции f(x) становится все ближе к значению L. Если такое значение существует, говорят, что функция имеет предел в точке a.

Важно, что f(x) может не быть определена в самой точке a, но нас интересует ее поведение вблизи этой точки.

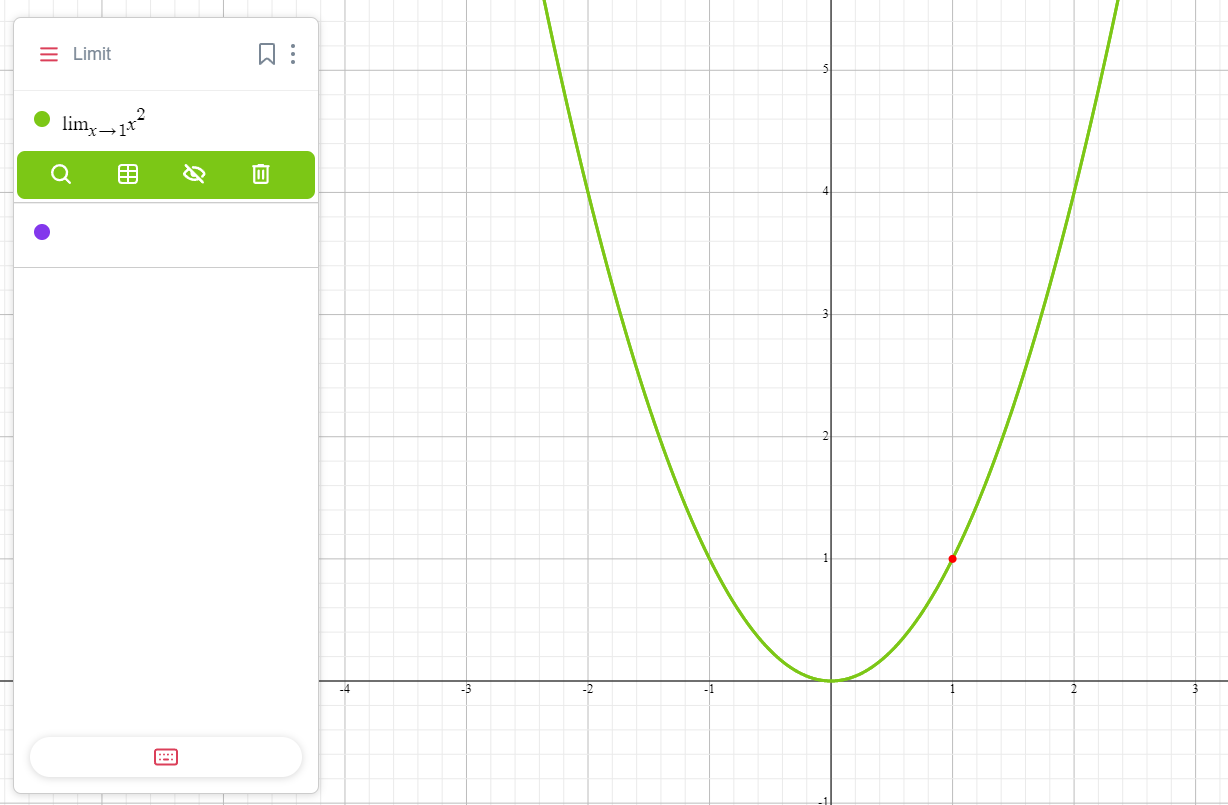
Пример. Нужно найти предел функции x2 . График f(x) = x²является параболой, которая проходит через точку (1,1). В этой точке, где x = 1, значение x²также равно 1.

\[ x^2 = 1^2 = 1 \]

Предел равен 1 (или L = 1). На графике это будет выглядеть так.

график функции икс в квадрате — График функции x²

Какие бывают виды пределов

Предел функции в точке

Предел функции в точке x₀ описывает поведение функции f(x), когда x приближается к x₀. Если при x→x₀ значение функции стремится к некоторому числу L, то считается, что функция имеет предел L в точке x₀:

\[ \lim_{x \to x_0} f(x) = L \]

Здесь важно учитывать, что пределы могут существовать как с одной стороны (слева или справа), так и с обеих.

Пример

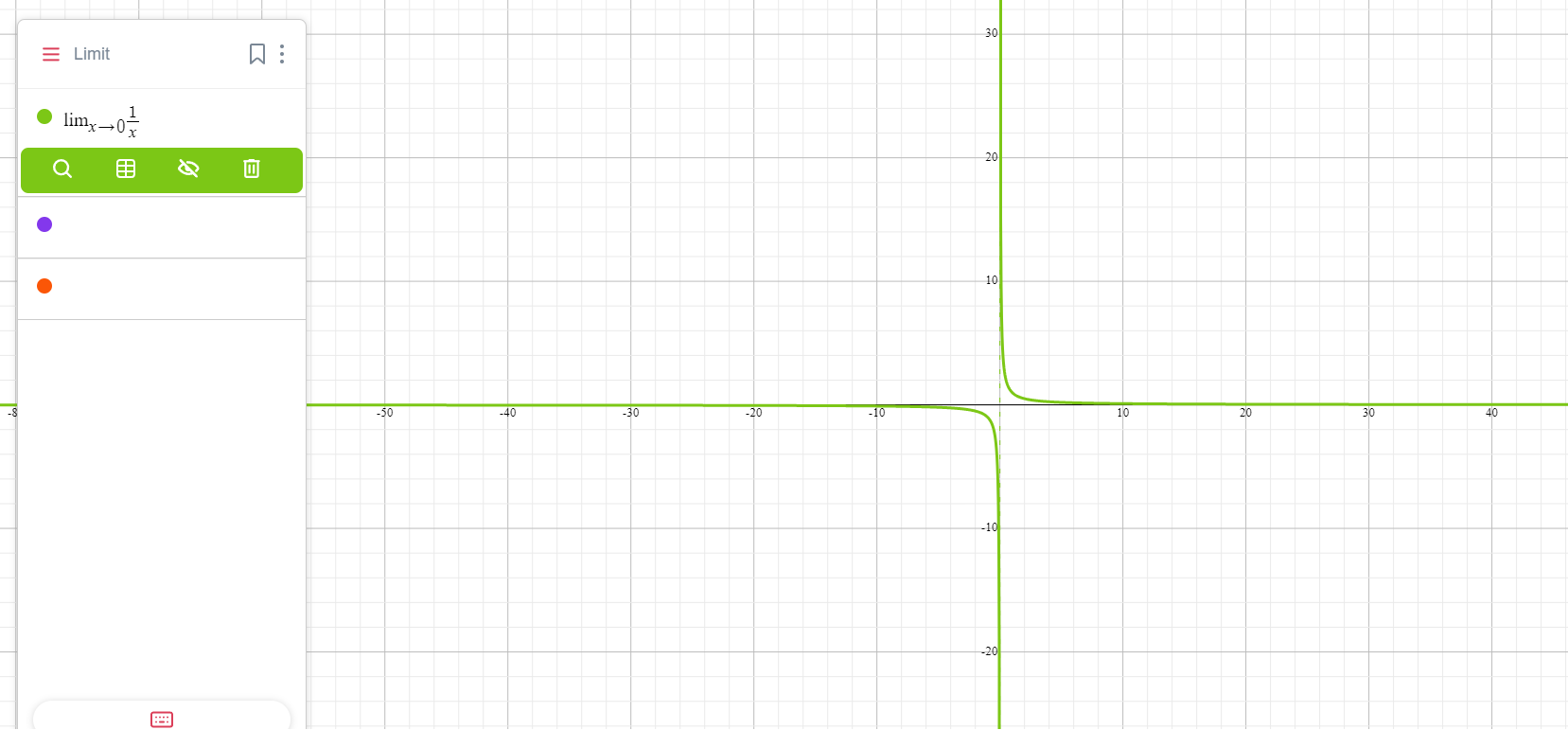
Функция $ f(x) = \frac{1}{x} $ имеет разрыв в точке x = 0, потому что пределы с разных сторон не равны:

\[
\begin{aligned}
\lim_{x \to 0^-} \frac{1}{x} &= -\infty \quad (\text{слева от } 0), \\
\lim_{x \to 0^+} \frac{1}{x} &= +\infty \quad (\text{справа от } 0).
\end{aligned}
\]

Здесь двусторонний предел не существует, так как пределы слева и справа не совпадают.

график предел функции в точке — График функции $ \lim_{x \to 0} \frac{1}{x} $

Предел функции на бесконечности

Предел на бесконечности описывает поведение функции, когда аргумент x стремится к +∞ или −∞. Если при x→∞ (или x→−∞) значение функции стремится к какому-то числу L, то считается, что функция имеет конечный предел на бесконечности:

$ \displaystyle \lim_{x \to \infty} f(x) = L \quad \text{или} \quad \lim_{x \to -\infty} f(x) = L $

Также возможна ситуация, когда функция не стремится к конечному числу, а растет или убывает бесконечно:

$ \displaystyle \lim_{x \to \infty} f(x) = \infty \quad \text{или} \quad \lim_{x \to -\infty} f(x) = -\infty $

Предел последовательности

Предел последовательности — это значение, к которому стремятся члены последовательности {a_n}, когда n→∞. Если a_n стремится к числу L при n→∞, то говорят, что последовательность имеет предел L:

$ \displaystyle \lim_{n \to \infty} a_n = L $

Это аналогично пределам функции на бесконечности, но уже для дискретного множества (с отдельными, целыми значениями аргументов).

Предел функции с неопределенностями

Иногда при вычислении пределов можно столкнуться с неопределенными выражениями, такими как $ \frac{0}{0} $ или $ \frac{\infty}{\infty} $.

В таких случаях необходимо применять дополнительные методы для вычисления пределов.

Виды неопределенности

Неопределенности возникают, когда прямое подставление значений приводит к неопределенной форме. Эти формы делают невозможным получение точного значения предела.

Вот основные неопределенности для большинства случаев:

1. $ \frac{0}{0} $

Наиболее распространенная неопределенность. В этом случае и числитель, и знаменатель стремятся к нулю. Пример:

$ \displaystyle \lim_{x \to 0} \frac{\sin(x)}{x} $

Для вычисления такого предела часто применяют правило Лопиталя или разложение функции в ряд Тейлора.

2. $ \frac{\infty}{\infty} $

Неопределенность, возникающая, когда и числитель, и знаменатель стремятся к бесконечности. Пример:

$ \displaystyle \lim_{x \to \infty} \frac{x^2}{e^x} $

Для устранения этой неопределенности также можно использовать правило Лопиталя.

3. ∞−∞

Неопределенность, возникающая, когда и числитель, и знаменатель стремятся к бесконечности. Пример:

$ (\sqrt{x^2 + x} — x) $

Для решения таких пределов часто используют приведение к общему знаменателю.

4. 0 * ∞

Неопределенность, когда один множитель стремится к нулю, а другой — к бесконечности. Пример:

$ x \cdot \ln(x) $

В таких случаях преобразуют произведение в отношение (например, $ \frac{1}{\frac{1}{x}} $) и уже после этого применяют правило Лопиталя.

5. 1∞

Неопределенность, возникающая, когда основание стремится к единице, а показатель степени — к бесконечности. Пример:

$ \left(1 + \frac{1}{x}\right)^x $

Для таких пределов используют логарифмирование выражения, а потом применяют правило Лопиталя.

6. 0⁰

Неопределенность, возникающая при возведении числа, стремящегося к нулю, в степень, также стремящуюся к нулю. Пример:

$ x^x $

Обычно такие пределы решают через логарифмирование или разложение в ряды.

∞⁰

Неопределенность, возникающая, когда основание стремится к бесконечности, а показатель — к нулю. Пример:

$ \frac{1}{x^x} $

Для таких выражений часто применяют логарифмирование и другие методы анализа функции.

Способы устранения неопределенности

Правило Лопиталя

Если предел имеет вид $ \frac{0}{0} $ или $ \frac{\infty}{\infty} $, то можно использовать производные функции:

$ \lim\limits_{x \to x_0} \frac{f'(x)}{g'(x)} $

при условии, что предел справа существует.

Применение: часто используется для дробей, где прямое подставление приводит к неопределенности.

Алгебраические преобразования

Упрощение выражения может помочь устранить неопределенность. Для этого можно:

— сократить дроби;

— умножить на сопряженное выражение;

— провести факторизацию многочленов.

Применение: например, $ \frac{x^2 — 4}{x — 2} $ можно упростить до $ (x + 2) $.

Применение: например, x2-4x-2 можно упростить до (x+2).

Разложение в ряд Тейлора

Функцию можно разложить в ряд Тейлора около точки c. Это позволяет выразить функцию через полиномы, что упрощает вычисление предела.

Применение: например, $ \sin x $ можно разложить как $ x — \frac{x^3}{6} + O(x^5) $ для $ x $, близкого к 0.

Как рассчитывать пределы функции

При вычислении пределов в математическом анализе используются несколько основных правил и методов. Разберем их подробнее.

Правила вычисления пределов в матанализе

Правило предельной линейности

$ (f(x) + g(x)) = f(x) + g(x) $

Предел суммы функций равен сумме пределов этих функций. То же самое верно для разности функций. Если вы можете найти пределы функций f(x) и g(x) при x, стремящемся к c, то можете сложить (или вычесть) эти пределы.

Пример: если $ f(x) = 3 $ и $ g(x) = 4 $,
то $ (f(x) + g(x)) = 3 + 4 = 7 $.

Правило предельного произведения

$ (f(x) \cdot g(x)) = f(x) \cdot g(x) $

Предел произведения двух функций равен произведению их пределов. Если обе функции стремятся к конечным значениям при x→c, то вы можете перемножить их пределы.

Пример: если $ f(x) = 2 $ и $ g(x) = 3 $, то $ (f(x) \cdot g(x)) = 2 \cdot 3 = 6 $.

Правило предельного деления

$ \frac{f(x)}{g(x)} = \frac{f(x)}{g(x)}, $ при условии, что $ g(x) \neq 0 $.

Это правило позволяет находить пределы дробей. Если предел числителя и предел знаменателя существуют и последний не равен нулю, то предел дроби равен отношению их пределов.

Пример: если $ f(x) = 6 $ и $ g(x) = 3 $, то $ \frac{f(x)}{g(x)} = \frac{6}{3} = 2 $.

Правило предельного возведения в степень

$ (f(x))^n = (f(x))^n $

Это правило позволяет находить пределы функций, возведенных в натуральную степень n. Если предел функции f(x) существует, то вы можете возвести его в степень.

Пример: если $ f(x) = 4 $, то $ (f(x))^2 = 4^2 = 16 $.

Правило предельного корня

$ \sqrt[n]{f(x)} = \sqrt[n]{f(x)} $

Предел корня n-й степени функции f(x) равен корню n-й степени ее предела. Оно применимо, когда предел функции f(x) положителен.

Пример: если $ f(x) = 16 $, то $ \sqrt{f(x)} = \sqrt{16} = 4 $.

Методы расчета предела функции

Метод прямой подстановки

Если функция f(x) непрерывна в точке c и подстановка x = c не приводит к неопределенности, можно просто подставить это значение.

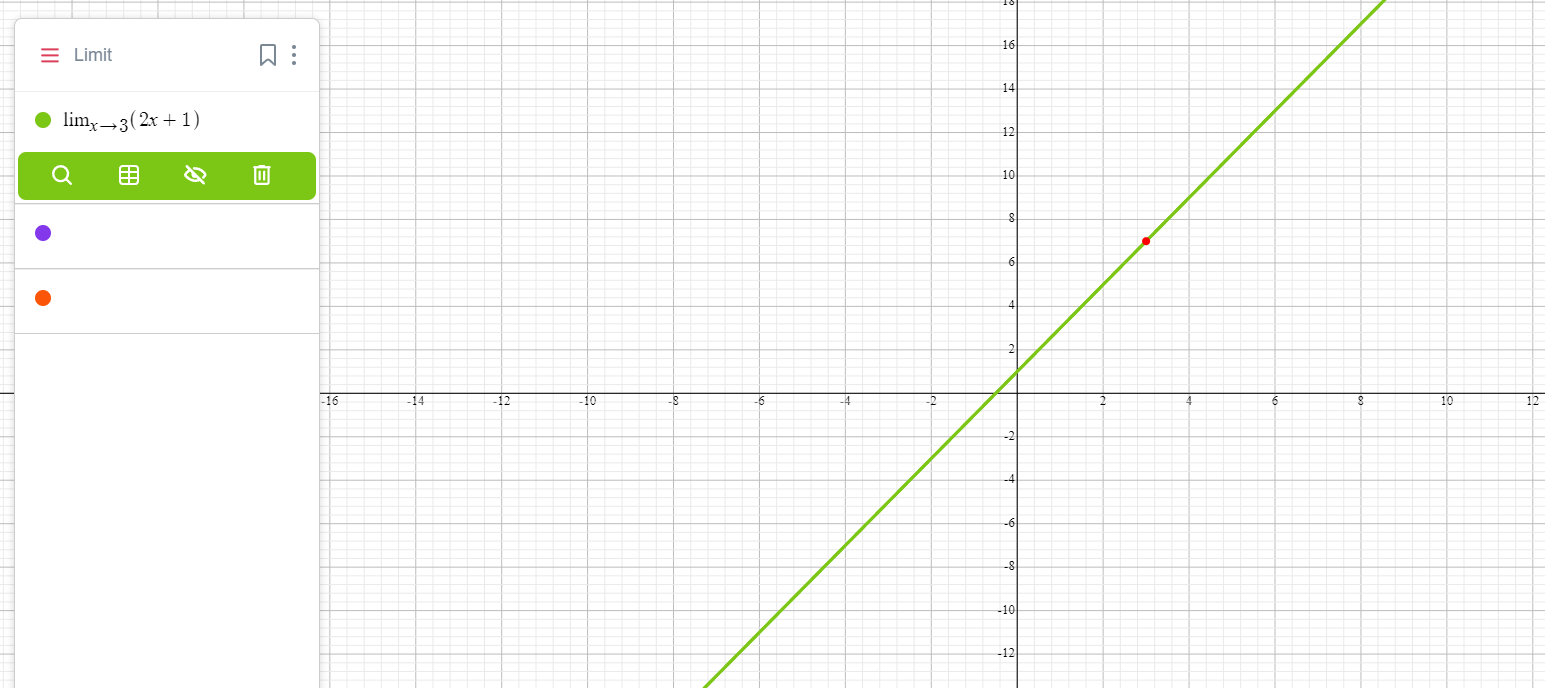
Пример

$ (2x + 1) = 2(3) + 1 = 6 + 1 = 7 $.

Метод прямой подстановки — График функции $ (2x + 1) $

Метод деления на старший член

Этот метод используется для пределов дробей, особенно когда обе части стремятся к бесконечности.

Пример:

$ \frac{3x^2 + 5x + 2}{4x^2 — 2} $

Делим все члены на x²:

$ \frac{3 + \frac{5}{x} + \frac{2}{x^2}}{4 — \frac{2}{x^2}} = \frac{3 + 0 + 0}{4 — 0} = \frac{3}{4} $

Метод деления на старший член — График функции $ \frac{3x^2 + 5x + 2}{4x^2 — 2} $

Метод сравнения с известными пределами

Применяется для упрощения вычисления предела, если можно сравнить его с известным пределом.

Пример:

$ \frac{\tan x}{x} $

Зная, что $ \tan x \sim x $ при $ x \to 0 $, можно сказать, что $ \frac{\tan x}{x} = 1 $.

Метод замены переменной

Можно использовать для упрощения выражения и приведения его к известной форме.

Пример:

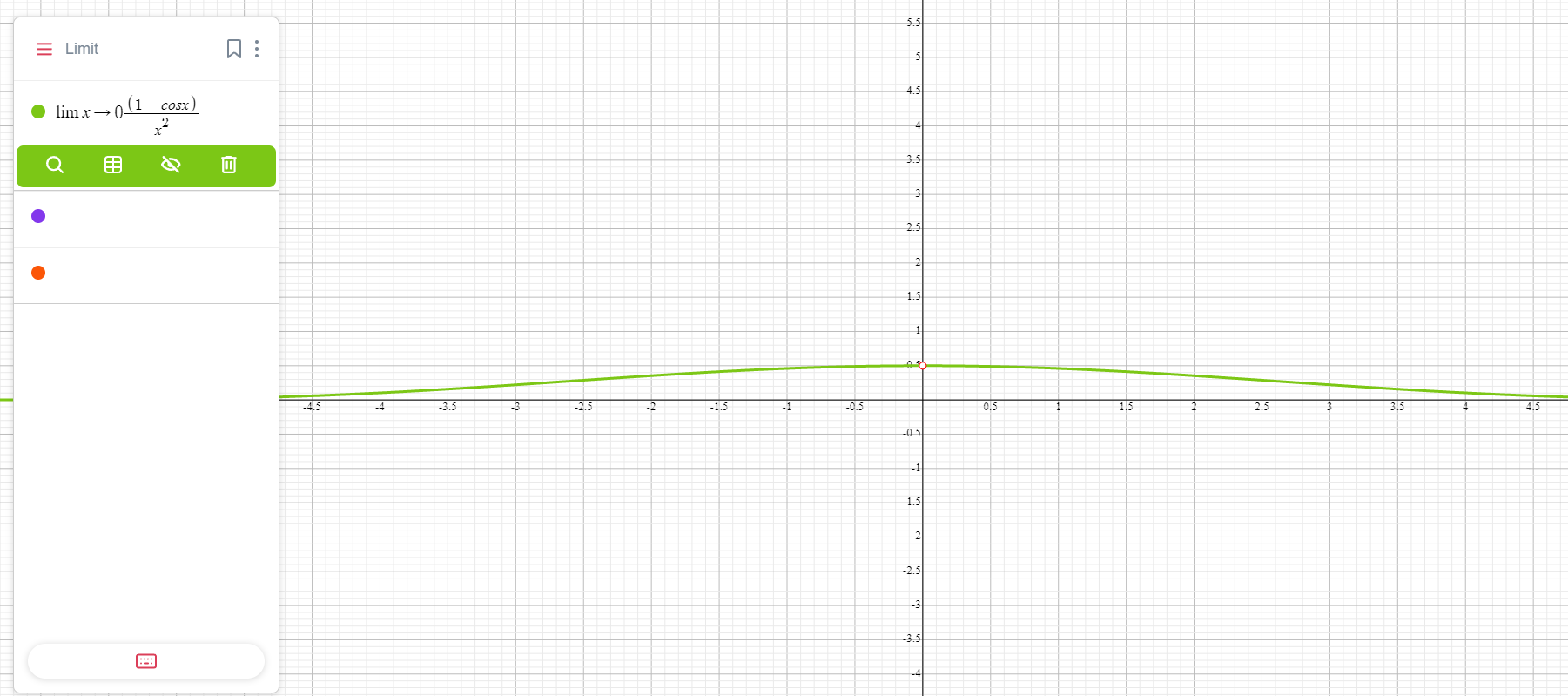
$ \frac{1 — \cos x}{x^2} $

Заменим $ x $ на $ 2t $:

$ \frac{1 — \cos(2t)}{(2t)^2} = \frac{1 — (1 — 2t^2)}{4t^2} = \frac{2t^2}{4t^2} = \frac{1}{2} $

Метод замены переменной — График функции $ \frac{1 — \cos x}{x^2} $

Как раскрывать неопределенности в вычислении пределов

Применение правила Лопиталя

Суть метода в том, что нужно взять производные числителя и знаменателя и найти предел их отношения.

Пример для неопределенности 0/0

$ \frac{\sin x}{x} $

Определяем, что при x = 0 получится неопределенность 0/0.
Находим производные согласно правилу Лопиталя:

— производная числителя: $ \frac{d}{dx} (\sin x) = \cos x $.

— производная знаменателя: $ \frac{d}{dx} (x) = 1 $.

Подставим производные в формулу:

$ \frac{\cos x}{1} = \cos(0) = 1 $.

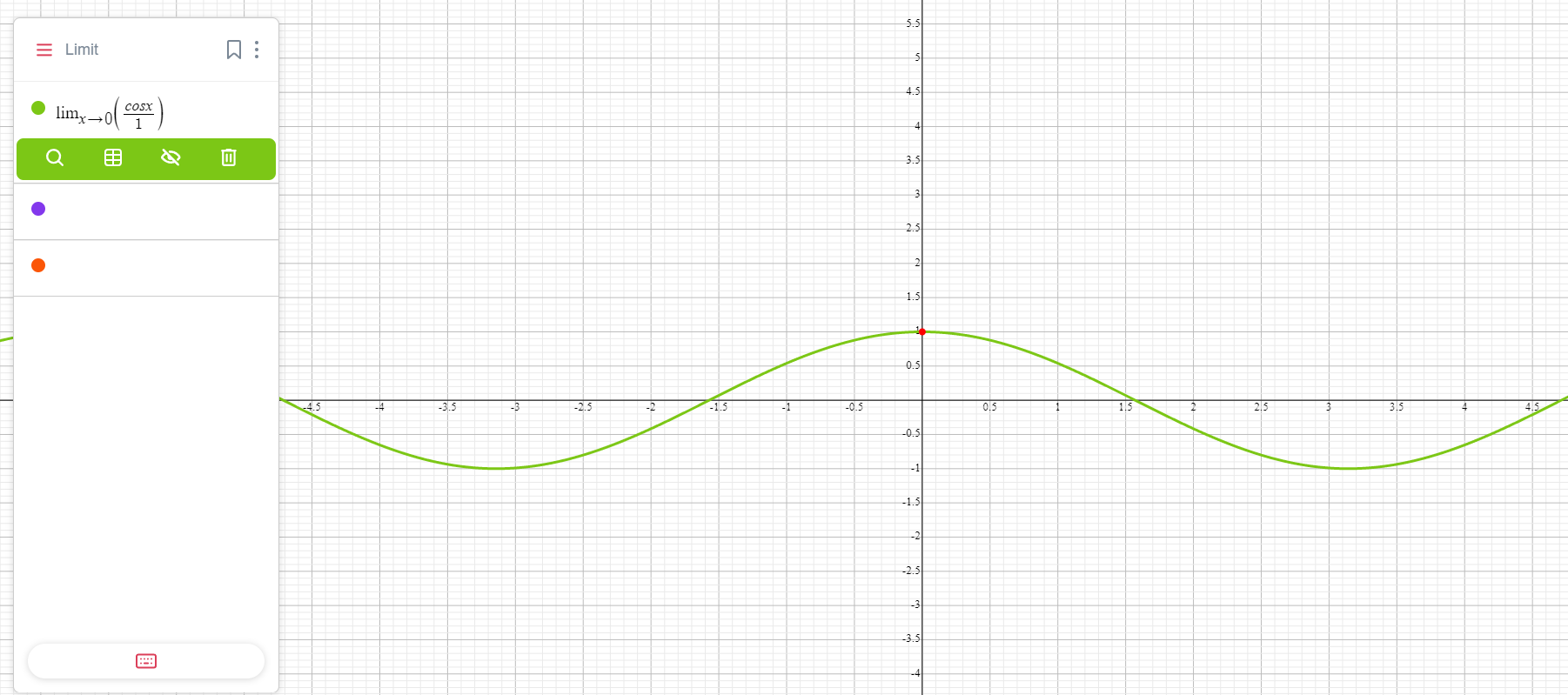
Лопиталя график — График функции $ \frac{\sin x}{x} $

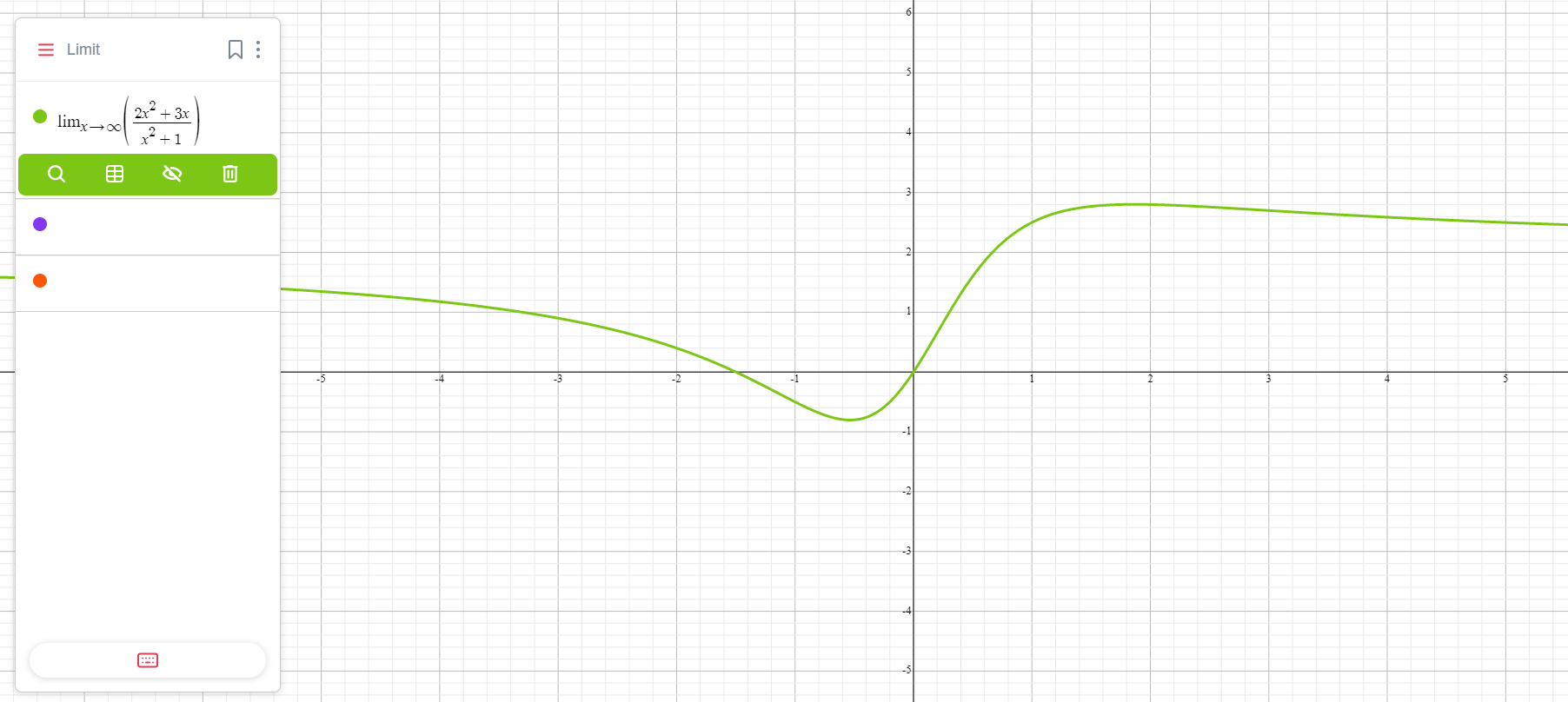
Пример для неопределенности ∞/∞

$ \frac{2x^2 + 3x}{x^2 + 1} $

Определяем, что при x→∞ получится неопределенность ∞/∞.
Применяем правило Лопиталя и находим производные:

— производная числителя: $ \frac{d}{dx} (2x^2 + 3x) = 4x + 3 $.

— производная знаменателя: $ \frac{d}{dx} (x^2 + 1) = 2x $.

Подставим производные:

$ \frac{4x + 3}{2x} = \frac{4 + \frac{3}{x}}{2} = \frac{4 + 0}{2} = 2 $.

график правила Лопиталя — График функции $ \frac{2x^2 + 3x}{x^2 + 1} $

Метод разложения в ряд Тейлора

Разложение функции в ряд Тейлора позволяет заменить ее на более простую функцию для вычисления предела.

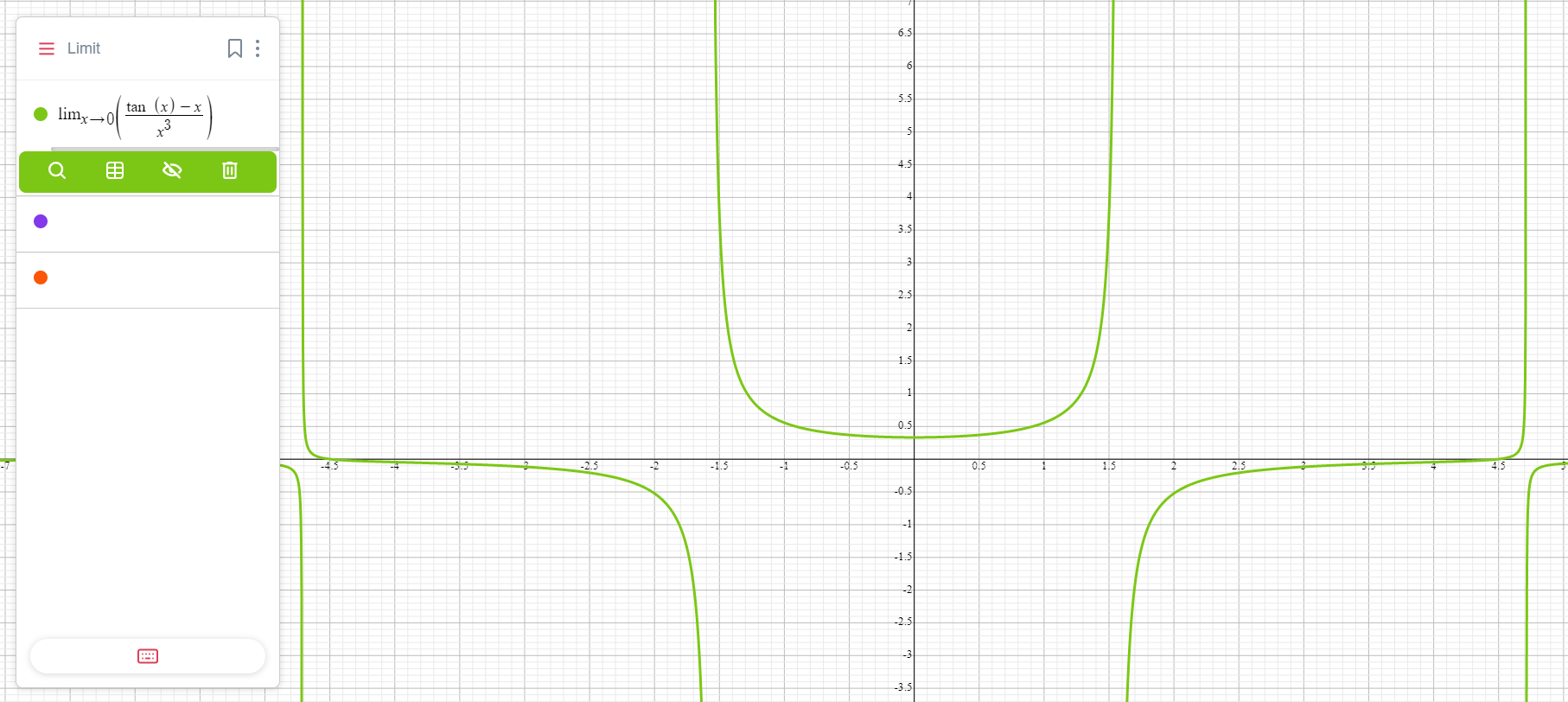
Пример разложения функции $ \frac{\tan x — x}{x^3} $

1. Разложим $ \tan x $ в ряд Тейлора

$\tan x = x + \frac{x^3}{3} + O(x^5)$.

Получается:

$\tan x — x \approx \frac{x^3}{3} + O(x^5)$.

2. Подставляем полученный результат в предел

$\frac{\frac{x^3}{3} + O(x^5)}{x^3} = \left(\frac{1}{3} + O(x^2)\right)$.

3. Находим предел

$\left(\frac{1}{3} + O(x^2)\right) = \frac{1}{3} + 0 = \frac{1}{3}$.

Метод разложения в ряд Тейлора — График функции $ \frac{\tan x — x}{x^3} $

1. Разложим $ \tan x $ в ряд Тейлора

$\tan x = x + \frac{x^3}{3} + O(x^5).$

Получается:

$\tan x — x \approx \frac{x^3}{3} + O(x^5).$

2. Подставляем полученный результат в предел

$\frac{\frac{x^3}{3} + O(x^5)}{x^3} = \left(\frac{1}{3} + O(x^2)\right).$

3. Находим предел

$\left(\frac{1}{3} + O(x^2)\right) = \frac{1}{3} + 0 = \frac{1}{3}.$

Где используют предел функции

У предела функции множество применений, например:

Определение непрерывности функции
Функция f(x) считается непрерывной в точке a, если предел функции в этой точке равен ее значению:

$ f(x) = f(a) $

Это означает, что значения функции приближаются к значению функции в точке a при стремлении x к a.

Нахождение производной

Пределы лежат в основе вычисления производной, которая определяет мгновенную скорость изменения функции. Производная f′(a) в точке a рассчитывается как предел отношения приращений.

$ f'(a) = \frac{f(a + h) — f(a)}{h}, $

где:

f(a) — значение функции в точке a;

f'(a) — производная функции f(x) в точке a, показывающая скорость изменения функции;

h — малое приращение, добавляемое к значению a, которое стремится к нулю;

f(a+h) — значение функции при x = a + h, то есть значение функции в точке, смещенной от a;

$\frac{f(a + h) — f(a)}{h}$ — отношение приращений, показывающее, насколько изменяется значение функции на единицу изменения $x$ при переходе от $a$ к $a + h$.

Вычисление интеграла

В теории интегралов пределы используются для вычисления площади под кривой. Определенный интеграл функции формируется на основе предела суммы площадей малых участков:

\[
\int_{a}^{b} f(x) \, dx = \sum_{i=1}^{n} f(x_i) \Delta x,
\]

где:

$\int_{a}^{b} f(x) \, dx$ — определенный интеграл функции f(x) от a до b, представляющий собой площадь под графиком функции на указанном интервале;

a — нижняя граница интегрирования, то есть значение x, с которого начинается интервал, на котором мы вычисляем площадь под графиком функции f(x);

b — верхняя граница интегрирования, то есть значение x, на котором заканчивается интервал;

n — количество равных подинтервалов, на которые делится интервал [a,b];

Δx = ^{b – a}⁄_n — ширина каждого подинтервала, которая стремится к нулю при n→∞;

x_i — точки, в которых вычисляется значение функции f(x) на каждом подинтервале. Это может быть левая, правая сторона или середина подинтервала;

$$\sum_{i=1}^{n} f(x_{i}) \Delta x$$ — сумма площадей всех подинтервалов, которая приближается к значению интеграла, то есть к точной площади под графиком функции. По мере увеличения n эта сумма стремится к точному значению интеграла.

Как используют пределы в IT

Пределы функций имеют прикладное значение, например:

в машинном обучении они помогают найти наименьшее значение ошибки, чтобы модель могла лучше обучаться и точнее делать прогнозы;
в компьютерной графике: разложения в ряды помогают рассчитать движение объектов, свет и тени. Благодаря этому графика рендерится быстрее и выглядит реалистично;
в обработке сигналов: вычисление пределов сглаживает резкие изменения, стабилизируя звук и изображение при фильтрации. Это важно для качественного воспроизведения аудио и видео;
в симуляциях и моделировании: пределы используются для учета мелких изменений, например при моделировании потока воды или движения частиц, что делает симуляции точнее;
в нейронных сетях: пределы помогают контролировать функции, которые при больших значениях могут становиться неустойчивыми и приводить к некорректным результатам.

Краткий гайд, как находить предел

Определите форму предела.

Подставьте значение x = c в функцию f(x).
Если получите определенное значение — это и есть предел.

Если получите неопределенность (например, $ \frac{0}{0}, \frac{\infty}{\infty}, \infty — \infty $ и т. д.), переходите к следующему шагу.

Попробуйте метод прямой подстановки.

Если функция непрерывна в точке, просто подставьте значение x = c.

Используйте алгебраические преобразования.

Если получаете неопределенность, попробуйте упростить выражение:

факторизация (например, для дробей);
деление на старший член, если работаете с многочленами.

Примените методы раскрытия неопределенности.

Если вы все еще получаете неопределенность, используйте способы раскрытия неопределенности, такие как правило Лопиталя или разложение в ряд Тейлора.

Сравнение с известными пределами.

Если выражение похоже на известный предел, используйте его для быстрого решения.

Замена переменной.

Если функция сложная, попробуйте заменить переменную для упрощения.

Онлайн-калькуляторы для нахождения пределов

Онлайн-сервисы могут значительно упростить процесс вычислений, особенно если пределы сложные или требуют применения нескольких методов, таких как правило Лопиталя или разложения в ряд Тейлора.

Вот несколько калькуляторов, которые помогут с расчетами:

WolframAlpha — помогает в решении математических задач. Нужно ввести запрос в поисковую строку, а система подготовит ответ или выдаст готовое решение.
Symbolab — покажет пошаговое решение с объяснением, как именно достигается результат. Можно автоматически рисовать графики.
Mathway — в формате диалога можно описать проблему, прикрепить фотографии или вставить формулы, которые нужно решить.
Integral Calculator — показывает расчеты пошагово, объясняет математические концепции, визуализирует уравнения.

Продвинутые научные исследования и практический опыт. Участвуйте в НИР под руководством опытных ученых, получите опыт на хакатонах и научитесь решать реальные бизнес-кейсы по анализу данных — на онлайн-магистратуре Skillfactory и ТГУ.

Науки о данных и машинное обучение