Временной ряд — это последовательность значений, которые протекают и измеряются в определенном временном промежутке. К бытовым примерам временного ряда можно отнести метеорологические наблюдения или колебания цен на рынке.
Аналитикам такие наборы данных позволяют выявлять закономерности, прогнозировать будущее и предлагать бизнесу обоснованные решения. В этой статье разберемся, с чего начать осваивать анализ временных рядов, вместе с Team Lead Data Scientist в VK, экспертом Эйч, Максимом Кулаевым.
Что такое временные ряды
Временные ряды можно представить как последовательность данных, которые фиксируются с определенной периодичностью. Зависимость от времени — их ключевая особенность. Она позволяет аналитикам выявлять тренды и сезонные колебания. Области применения такого анализа самые разнообразные: экономика, финансы, маркетинг.
Временные ряды помогают специалистам ответить на вопросы, что происходило в прошлом и что может случиться в будущем. С их помощью аналитики могут:
- Выявлять тренды и закономерности.
- Строить модели и прогнозировать будущее.
- Оптимизировать процессы.
Компоненты временного ряда
Каждый временной ряд состоит из нескольких компонентов:
- Тренд — долгосрочная тенденция. Например, устойчивый рост спроса на электроавтомобили.
- Сезонность — повторяющиеся изменения, связанные, как правило, с календарными изменениями: сменой времен года или наступлением праздничных дней.
- Цикличность — колебания, обусловленные экономическими циклами или циклами деловой активности. Период такого колебания в среднем составляет от двух до пяти лет.
- Случайные колебания — ситуативные изменения, которые нельзя предсказать, например неожиданные события или технические сбои.
Эти компоненты накладываются друг на друга. Задача анализа в том, чтобы понять, что конкретно влияет на данные. Для этого аналитики используют декомпозицию — анализ временного ряда путем разложения его на отдельные компоненты.
Типы временных рядов
Предполагается, что данные временного ряда собираются регулярно, что в действительности не всегда возможно. Поэтому аналитики делят ряды на две большие группы: регулярные и нерегулярные.
Данные регулярных рядов обладают систематическим характером. Нерегулярные ряды, напротив, собирают с разными интервалами времени — например, пополнения банковской карты.
Также для подготовки данных к анализу и выбору методов аналитики различают следующие виды временных рядов.
Стационарные и нестационарные временные ряды
Стационарность — ключевое свойство ряда, необходимое для использования большинства «классических» методов анализа. Если данные нестационарны, анализ может быть неточным или вообще не привести к результатам.
Свойства стационарного ряда:
- У ряда отсутствует тренд.
- У ряда отсутствует сезонность.
- У ряда не изменяется дисперсия — расстояние временного ряда от среднего значения.
Для проверки стационарности аналитики также используются специальные тесты: критерий Дики–Фуллера или KPSS.
Согласно тесту Дики–Фуллера, если p-value значение теста меньше α, то ряд стационарен. Реализация теста есть в Python в пакете statsmodels:
import statsmodels.api as sm
p = sm.tsa.stattools.adfuller(df.time_series)[1]
print(f'Критерий Дики-Фуллера: p-value={p}')
Разберемся, как подготовить данные к анализу и что делать, если временной ряд не стационарен.
Как подготовить данные временного ряда к анализу
Анализ временного ряда начинается с подготовки данных. Это важный этап, без которого результаты анализа могут быть ошибочными.
Подготовка данных включает несколько ключевых этапов:
1. Проверка на полноту. Если данные отсутствуют, их нужно заполнить.
2. Корректность значений. Нужно избавить ряд от аномалий, которые могут указывать на ошибки ввода.
3. Приведение к стационарности. Многие модели анализа работают только со стационарными рядами, где основные статистические свойства (среднее, дисперсия) остаются неизменными.
Заполнение пропусков временного ряда

Существует несколько основных способов заполнить пропуски временных рядов. Какой из них лучше использовать, зависит от структуры данных и цели анализа. Рассмотрим их краткое описание:
1. Заполнение средним или медианным значением
Метод подходит, если пропуски в ряду случайны и данные имеют однородное распределение. Тогда можно заменить пропуски средним значением или медианой столбца. Подход теряет точность при наличии трендов или сезонности.
2. Использование предыдущих или последующих значений
Данные временного ряда статистически взаимосвязаны, это называется автокорреляционной функцией временного ряда. Эта взаимосвязь делает возможным заполнение пропусков предыдущими или последующими значениями. Тем не менее многократное применение одного значения может исказить тренды, поэтому стоит ограничивать количество заполняемых подряд пропусков.
3. Метод скользящего среднего
Для заполнения пропусков ряда также можно использовать скользящее среднее или медиану. Такой подход позволяет учесть тренды или локальные колебания, избегая грубых искажений.
4. Интерполяция
Интерполяция — это наиболее сложный метод из перечисленных. В сущности, это математическая попытка вычислить функцию, которая проходит через известные данные. Различают линейную, полиномиальную интерполяцию и сплайн. Линейная интерполяция предполагает построение прямой линии между точками на графике, тогда как полиномиальная и сплайн-интерполяция дают больше гибкости для описания сложных зависимостей.
Преобразование нестационарного временного ряда
Для обработки нестационарного временного ряда следует устранить проблему изменяющейся во времени дисперсии. Популярным методом является логарифмирование ряда.
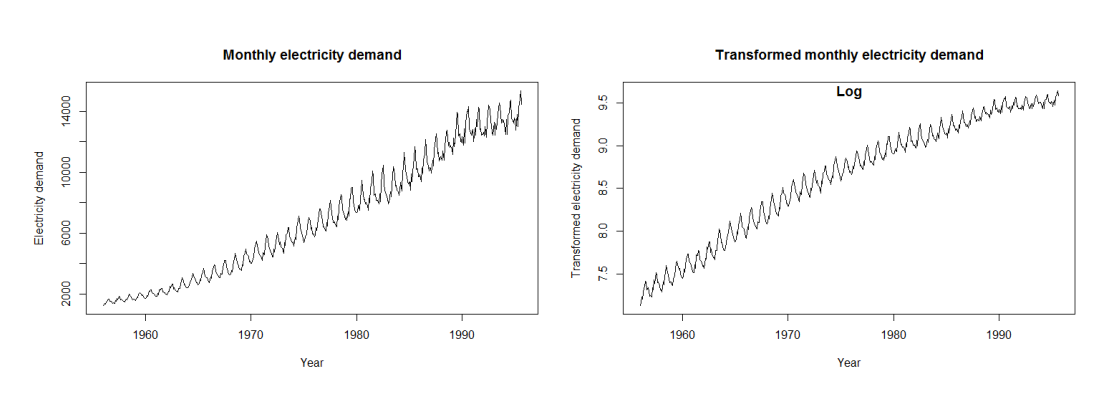
Более универсальный метод работы с рядом — преобразование Бокса–Кокса. Метод позволяет стабилизировать дисперсию и сделать ряд более пригодным для анализа.
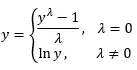
Перед применением преобразования нужно определить λ. И если λ = 0, то применяется логарифмирование.
from scipy import stats from scipy.special import inv_boxcox # Преобразование time_series, lambda = stats.boxcox(time_series) # Обратное преобразование time_series = inv_boxcos(time_series, lambda)
После стабилизации дисперсии стоит устранить сезонность. Это можно сделать посредством дифференцирования. Рассмотрим реализацию дифференцирования в библиотеке pandas на Python, для данных с сезонностью в 12 месяцев:
- Вычитаем из ряда этот же ряд, смещенный на длину периода.
Важно: в результате сдвигов в новом ряде появятся пропуски (NaN).
- Если после дифференцирования в данных остается сезонность, можно провести еще одно дифференцирование, но уже с новым рядом:
df['time_series_s_diff'] = df.time_series - df.time_series.shift(12) df['time_series_s_diff2'] = df.time_series_s_diff- df.time_series_s_diff.shift(12)
После устранения сезонности из ряда необходимо убрать тренд. Это также делается посредством дифференцирования: из текущего значения ряда вычитается предыдущее значение, смещенное на один шаг:
df['time_series_diff'] = df.time_series_s_diff2 - df.time_series_s_diff2.shift(1)
При необходимости преобразование можно повторять несколько раз.
Данные шаги последовательно приводят временной ряд к стационарному виду, что облегчает его анализ и прогнозирование.
Методы анализа временных рядов
Для анализа временных рядов существует длинный список методов, выбор которых зависит от задач.
Модели ARMA, ARIMA, SARIMA
ARMA и ARIMA были впервые применены для обработки сигналов во Второй мировой войне и стали широко использоваться в статистике и экономике с 1970-х годов.
ARMA, или Autoregressive Moving Average, сочетает авторегрессию (AR) и скользящее среднее (MA).
- Авторегрессия (AR) предполагает, что будущее значение переменной зависит от ее прошлых значений.
- Скользящее среднее (MA) оценивает влияние прошлых ошибок прогноза на текущие значения.
ARIMA, или Autoregressive Integrated Moving Average, — это расширенная версия ARMA. В эту модель включен компонент интеграции (I). Он относится к различным методам вычисления разницы между последовательными наблюдениями для получения стационарного процесса из нестационарного.
В случае, если временные ряды имеют выраженные сезонные компоненты, аналитики используют SARIMA (Seasonal ARIMA). Модель добавляет сезонные параметры к модели ARIMA и учитывает повторяющиеся паттерны, например ежемесячные или годовые изменения.
Экспоненциальное сглаживание
Метод экспоненциального сглаживания использует взвешенное среднее значение временного ряда для прогнозирования. Ключевая идея метода: большее значение при прогнозировании отдается более свежим наблюдениям. Это помогает строить эффективные долгосрочные прогнозы:
a (alfa) — коэффициент сглаживания, который принимает значения от 0 до 1. Он определяет, насколько продолжительность изменит существующие значения в базе данных;
x — текущее значение временного ряда (например, объем продаж);
y — сглаженная величина на текущий период;
t — значение тренда за предыдущий период.
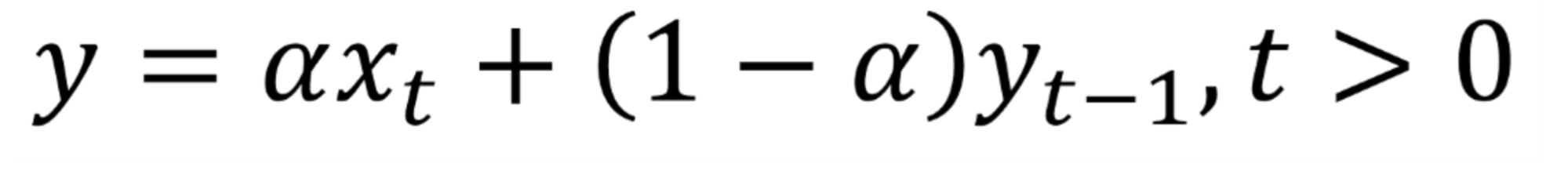
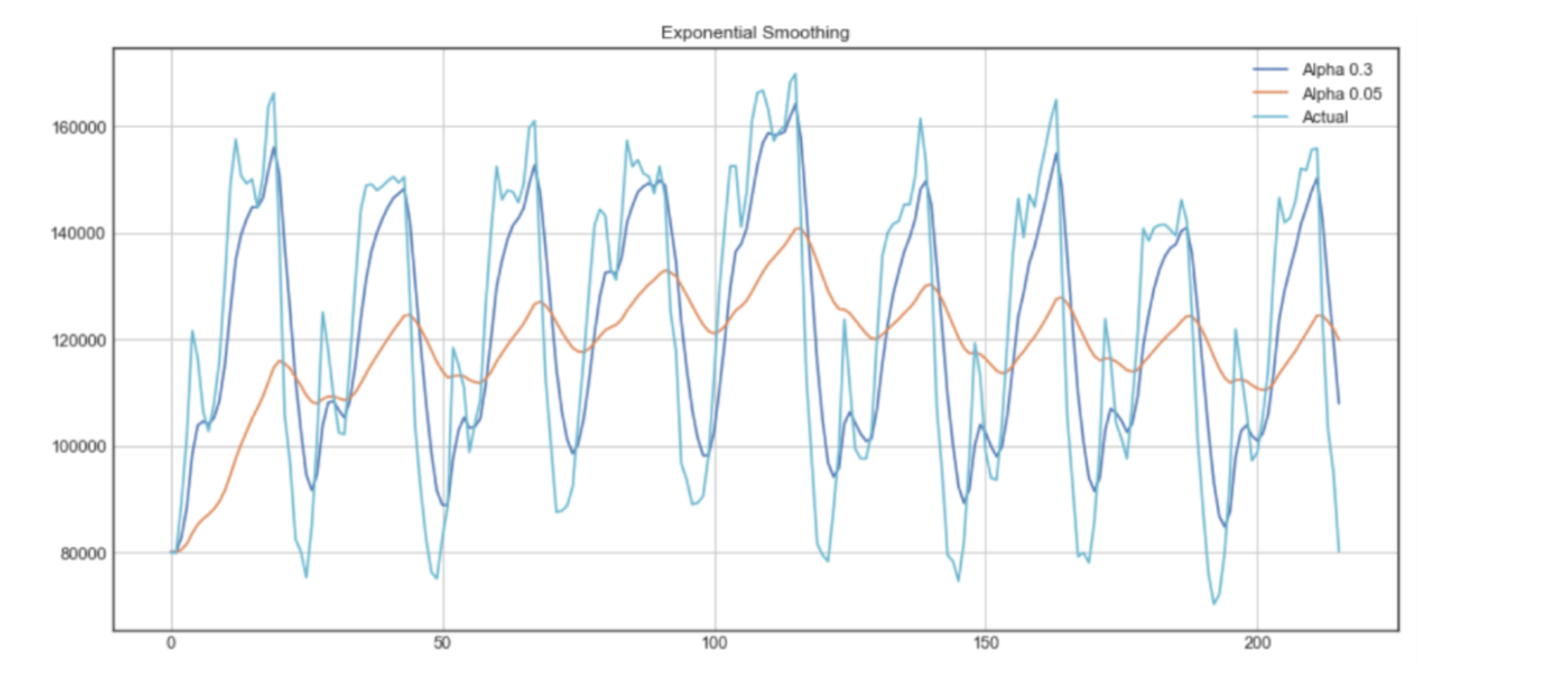
На графике экспоненциальное сглаживание представлено темно-синей линией временного ряда с коэффициентом сглаживания 0,3, а оранжевая линия использует коэффициент сглаживания 0,05. Чем меньше коэффициент сглаживания, тем более плавным будет временной ряд. Следовательно, когда коэффициент сглаживания приближается к 0, мы подходим к модели скользящего среднего.
Итоги. С чего начать изучение анализа временных рядов?
- Изучить виды временных рядов и их компоненты: тренды, сезонность и случайные колебания. Знание этих элементов поможет правильно интерпретировать данные и выявлять закономерности. Отдельное внимание стоит уделять стационарности временных рядов.
- Освоить методы подготовки данных. К таким относится заполнение пропусков, корректировка аномалий и преобразование данных в стационарный вид. Это поможет избежать искажений в анализе.
- Познакомиться с моделями ARMA, ARIMA и SARIMA.
- Изучить экспоненциальное сглаживание. Это нужно для создания долгосрочных прогнозов.
- Практиковаться на реальных данных с помощью популярных библиотек, таких как pandas и statsmodels.









