Алгоритм

Алгоритм — это четкая последовательность действий, выполнение которой дает какой-то заранее известный результат. Простыми словами, это набор инструкций для конкретной задачи. Известнее всего этот термин в информатике и компьютерных науках, где под ним понимают инструкции для решения задачи эффективным способом.

Сейчас под этим словом понимают любые последовательности действий, которые можно четко описать и разделить на простые шаги и которые приводят к достижению какой-то цели. Например, пойти на кухню, налить воду и положить в нее пакетик чая — это алгоритм для выполнения задачи «Заварить чай».

Алгоритмы в информатике — инструкции для компьютеров, набор шагов, который описывается программным кодом. Существуют конкретные алгоритмы для тех или иных действий, причем некоторые из них довольно сложные. Одна из целей использования алгоритмов — делать код эффективнее и оптимизировать его.

Кто пользуется алгоритмами

В общем смысле — абсолютно все живые и некоторые неживые существа, потому что любую последовательность действий, ведущую к цели, можно считать алгоритмом. Поиск еды животным — алгоритм, движения робота тоже описываются алгоритмом.

В узком смысле, в котором понятие используется в компьютерных науках, алгоритмами пользуются разработчики, некоторые инженеры и аналитики, а также специалисты по машинному обучению, тестировщики и многие другие. Это одно из ключевых понятий в IT.

Для чего нужны алгоритмы

Алгоритмы в информатике нужны для эффективного решения различных задач, в том числе тех, выполнение которых «в лоб» имеет высокую сложность или вовсе невозможно. На практике существуют алгоритмы практически для чего угодно: сортировки, прохождения по структурам данных, поиска элементов, фильтрации информации, математических операций и так далее.

Например, отсортировать массив можно в ходе полного перебора — это самое очевидное решение. А можно воспользоваться алгоритмом быстрой сортировки: он сложнее и не так очевиден, зато намного быстрее работает и не так сильно нагружает мощности компьютера. Строго говоря, полный перебор — это тоже алгоритм, но очень простой.

Существуют алгоритмически неразрешимые задачи, для решения которых нет и не может существовать алгоритма. Но большинство задач в IT разрешимы алгоритмически, и алгоритмы активно используются в работе с ними.

Алгоритмы применяются во всех направлениях IT и во многих других отраслях. Инструкции для автоматизированного станка или линии производства — алгоритмы, рецепт блюда — тоже.

Алгоритмизация

Алгоритмизация — это процесс разработки и описания последовательности шагов, которые необходимо выполнить для решения определенной задачи или достижения конкретной цели. Алгоритмизация является ключевым этапом при программировании и разработке программного обеспечения.

При алгоритмизации задачи создаются четкие инструкции, которые компьютер может понять и выполнять. Алгоритмы могут быть записаны в виде текстового описания, блок-схемы, псевдокода или других формализованных представлений. Они служат основой для написания кода программы, который позволяет компьютеру автоматически решать задачи в соответствии с предварительно разработанными инструкциями.

Алгоритмизация играет важную роль в информатике и программировании, так как хорошо разработанные алгоритмы обеспечивают эффективное и корректное выполнение задач, а также упрощают процесс отладки и поддержки программного кода.

Основные свойства алгоритмов

Дискретность. Алгоритм — не единая неделимая структура, он состоит из отдельных маленьких шагов, или действий. Эти действия идут в определенном порядке, одно начинается после завершения другого.

Результативность. Выполнение алгоритма должно привести к какому-либо результату и не оставлять неопределенности. Результат может в том числе оказаться неудачным — например, алгоритм может сообщить, что решения нет, — но он должен быть.

Детерминированность. На каждом шаге не должно возникать разночтений и разногласий, инструкции должны быть четко определены.

Массовость. Алгоритм обычно можно экстраполировать на похожие задачи с другими исходными данными — достаточно поменять изначальные условия. Например, стандартный алгоритм по решению квадратного уравнения останется неизменным вне зависимости от того, какие числа будут использоваться в этом уравнении.

Понятность. Алгоритм должен включать только действия, известные и понятные исполнителю.

Конечность. Алгоритмы конечны, они должны завершаться и выдавать результат, в некоторых определениях — за заранее известное число шагов.

Виды алгоритмов и примеры

Несмотря на слово «последовательность», алгоритм не всегда описывает действия в жестко заданном порядке. Особенно это актуально сейчас, с распространением асинхронности в программировании. В алгоритмах есть место для условий, циклов и других нелинейных конструкций. Перечислим основные типы алгоритмов.

Линейные

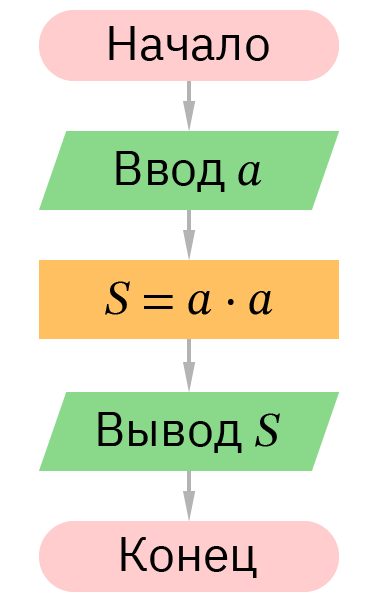
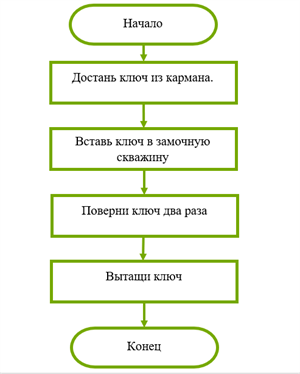
Это самый простой тип алгоритма: действия идут друг за другом, каждое начинается после того, как закончится предыдущее. Они не переставляются местами, не повторяются, выполняются при любых условиях.

Пример: обработка запроса на сервере перед логированием

1. Принять HTTP-запрос от клиента.
2. Извлечь данные из тела запроса.
3. Провалидировать данные (например, проверить, что email не пустой).
4. Сформировать объект для логирования.
5. Записать этот объект в лог-файл.
6. Вернуть клиенту ответ 200 OK.

То же самое в коде:

def handle_request(request):
    data = request.json()             # 1. получили данные
    validate(data)                    # 2. проверили
    log_entry = format_log(data)      # 3. сформировали лог
    write_to_log(log_entry)           # 4. записали
    return {"status": "ok"}           # 5. отправили ответ

Ветвящиеся

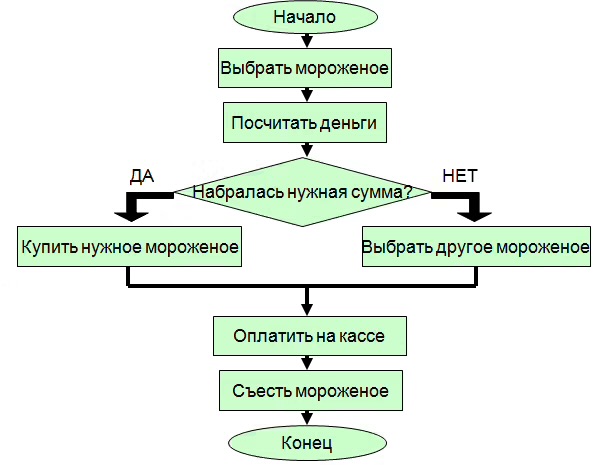
В этом типе алгоритма появляется ветвление: какие-то действия выполняются, только если верны некоторые условия. Например, если число меньше нуля, то его нужно удалить из структуры данных. Можно добавлять и вторую ветку: что делать, если условие неверно — например, число больше нуля или равно ему. Условий может быть несколько, они могут комбинироваться друг с другом.

Пример: авторизация пользователя

1. Пользователь вводит логин и пароль.
2. Система ищет пользователя в базе.
3. Если пользователь найден:
   – Сравнить введённый пароль с хешем.
   – Если пароль совпадает: впустить в систему.
   – Иначе: показать ошибку «неверный пароль».
4. Если пользователь не найден:
   – предложить зарегистрироваться или восстановить доступ.

Пример в псевдо-коде:

def login(user_input):
    user = find_in_db(user_input.login)

    if user:
        if check_password(user_input.password, user.hash):
            return "Добро пожаловать!"
        else:
            return "Неверный пароль"
    else:
        return "Пользователь не найден, создайте аккаунт"

Циклические

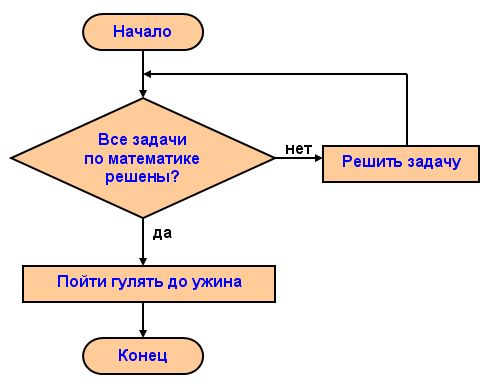
Такие алгоритмы выполняются в цикле. Когда какой-то блок действий заканчивается, эти действия начинаются снова и повторяются некоторое количество раз. Цикл может включать в себя одно действие или последовательность, а количество повторений может быть фиксированным или зависеть от условия: например, повторять этот блок кода, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечным.

Пример: обработка очереди задач в фоновом сервисе

1. Сервис обращается к очереди (например, RabbitMQ или Kafka).
2. Пока в очереди есть сообщения:
   – взять первое сообщение;
   – распарсить данные;
   – выполнить действие (например, отправить письмо или обновить статус заказа);
   – записать результат в лог;
3. Вернуться к началу цикла и снова проверить очередь.

В коде:

while queue.has_messages():
    msg = queue.get()
    data = parse(msg)
    process(data)
    log("done:", data)

Рекурсивные

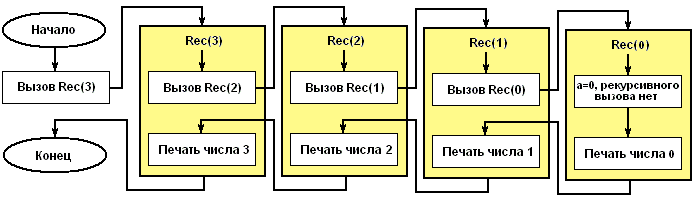
Рекурсия — это явление, когда какой-то алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные другие, но «экземпляров» работающих программ несколько, а не одна. Известный пример рекурсивного алгоритма — расчет чисел Фибоначчи.

Рекурсия позволяет изящно решать некоторые задачи, но с ней надо быть осторожнее: такие алгоритмы могут сильно нагружать ресурсы системы и работать медленнее других.

Пример: обход дерева директорий

Система должна пройтись по всем файлам и папкам в каталоге.

1. Берем папку.
2. Для каждого элемента внутри:
   – если это файл → обработать файл;
   – если это папка → вызвать алгоритм снова для этой вложенной папки.
3. Продолжать, пока не достигнем папок, в которых нет других директорий.

В коде:

import os

def walk_directory(path):
    for item in os.listdir(path):
        full_path = os.path.join(path, item)

        if os.path.isfile(full_path):
            print("Файл:", full_path)
        else:
            walk_directory(full_path)   # рекурсивный вызов

Вероятностные

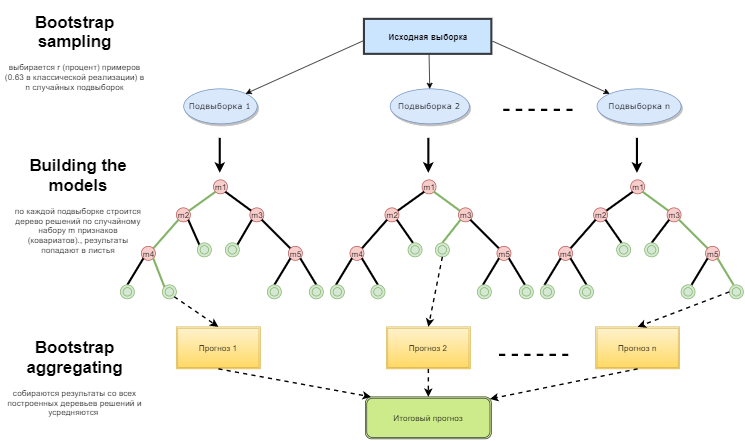
Такие алгоритмы упоминаются реже, но это довольно интересный тип: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним, например, относятся известные алгоритмы Лас-Вегас и Монте-Карло.

Пример: выбор ближайшего сервера через Randomized Load Balancing

Допустим, у вас есть несколько серверов, и нужно распределять запросы так, чтобы система была устойчивой к нагрузкам. Один из подходов — randomized load balancing:

1. Балансировщик выбирает случайных два сервера из пула.
2. Из этих двух выбирает тот, на котором меньше текущая нагрузка.
3. Отправляет запрос туда.

Почему это вероятностный алгоритм?

– На первом шаге используется случайный выбор, поэтому поведение алгоритма непредсказуемо заранее.
– Но в среднем этот подход сильно разгружает систему — и работает быстрее, чем детальный анализ всех серверов.

В коде:

import random

def choose_server(servers):
    # servers — список серверов вида {"name": "...", "load": число}
    s1, s2 = random.sample(servers, 2)  # случайный выбор двух серверов
    return s1 if s1["load"] < s2["load"] else s2

Основные и вспомогательные

Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный решает подзадачу и может использоваться внутри основного — для этого там просто указываются его название и входные данные. Пример вспомогательного алгоритма — любая программная функция.

Пример: загрузка пользовательского аватара в веб-приложении

Основной алгоритм: загрузка файла

1. Принять изображение от пользователя.
2. Проверить размер и формат.
3. Передать картинку во вспомогательную функцию обработки.
4. Сохранить обработанное изображение в хранилище.
5. Вернуть ссылку на аватар.

Вспомогательный алгоритм: ресайз изображения

1. Открыть изображение.
2. Уменьшить до нужных размеров (например, 256×256).
3. Сжать до нужного качества.
4. Вернуть оптимизированный файл.

В коде:

from PIL import Image

def resize_image(path):
    img = Image.open(path)
    img = img.resize((256, 256))
    img.save(path)
    return path


def upload_avatar(file):
    # основной алгоритм
    if file.size > 3 * 1024 * 1024:
        return "Файл слишком большой"

    saved_path = save_to_temp(file)

    # вспомогательный алгоритм
    processed_path = resize_image(saved_path)

    final_path = save_to_storage(processed_path)
    return final_path

Продвинутые алгоритмы

Для тех, кто хочет познакомиться с алгоритмами глубже, делимся продвинутыми и сложными примерами для продолжающих.

Алгоритм Евклида: простой способ найти НОД

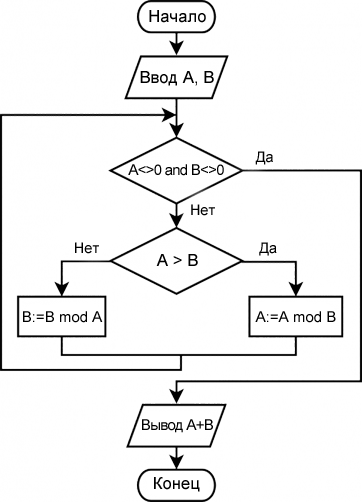
Алгоритм Евклида — один из самых известных и элегантных методов вычисления наибольшего общего делителя (НОД) двух целых чисел. Он назван в честь Евклида, который описал его в «Началах» более двух тысяч лет назад. Несмотря на возраст, алгоритм до сих пор используется в криптографии, оптимизациях и работе с числами в программировании.

Существует две основные версии алгоритма: через деление и через вычитание. В практике разработки чаще используют вариант с делением — он быстрее и короче.

Как работает алгоритм Евклида через деление

1. Берут два числа и делят большее на меньшее.
2. Если остатка нет — меньшее число и есть НОД.
3. Если остаток есть — заменяют большее число на этот остаток.
4. Возвращаются к первому шагу и повторяют процесс, пока остаток не станет равен нулю.

Идея проста: на каждом шаге мы уменьшаем задачу, пока не придtм к числу, которое делит оба исходных без остатка. Именно оно и является наибольшим общим делителем.

Пример: генерация ключей в криптографии (RSA)

При создании RSA-ключей нужно выбрать число e, которое будет взаимно простым с φ(n) — функцией Эйлера. Чтобы проверить это, используют алгоритм Евклида или его расширенную версию.

Как используют алгоритм:

1. Генерируются два больших простых числа p и q.
2. Считается φ(n) = (p−1)(q−1).
3. Нужно убедиться, что выбранное число e и φ(n) не имеют общих делителей, то есть НОД(e, φ(n)) = 1.
4. Чтобы проверить НОД, вызывают алгоритм Евклида.
5. Если НОД не равен 1 — выбирают другое e.

В коде:

# Алгоритм Евклида для поиска НОД
def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

# Пример проверки взаимной простоты e и phi_n
def is_valid_e(e, phi_n):
    return gcd(e, phi_n) == 1

phi_n = 120
e = 17

if is_valid_e(e, phi_n):
    print("Число e подходит для RSA")
else:
    print("Нужно выбрать другое e")

Перебор делителей («тестирование простоты»)

Алгоритм перебора делителей — один из самых базовых способов проверить, является ли число простым. Он перебирает возможные делители и смотрит, делится ли число без остатка. Метод кажется примитивным, но именно он лежит в основе многих более сложных алгоритмов и полезен там, где требуется простая и надежная проверка.

Как работает алгоритм

1. Берут число n, которое нужно проверить.
2. Перебирают все целые числа d от 2 до √n.
3. Если для какого-то d выполняется n mod d = 0, значит число составное.
4. Если делителей не нашлось — число простое.

Почему проверяют только до квадратного корня?
Если n имеет делитель больше √n, то второй делитель обязательно меньше √n — его мы бы уже нашли. Это сильно сокращает количество проверок.

Алгоритм подходит для небольших чисел и часто используется:

• в проверках на бэкенде, когда нужно быстро и просто протестировать число;
• как вспомогательный шаг в алгоритмах факторизации и криптографии;
• при работе с генерацией случайных простых чисел для тестов.

Пример: проверка кандидатов на простые числа при генерации тестовых данных

Во многих проектах (особенно связанных с криптографией, аналитикой или моделированием) нужно генерировать большие объёмы тестовых данных. Например, сервису требуется список случайных простых чисел для нагрузочного тестирования алгоритмов шифрования. Для простоты и скорости разработки выбирают самый надёжный базовый метод — перебор делителей.

Как это работает

1. Приложение генерирует случайное число в нужном диапазоне.
2. Перед добавлением в тестовый набор нужно проверить, простое оно или нет.
3. Для этого вызывают алгоритм перебора делителей:
   – перебирают числа от 2 до √n;
   – если ни одно не делит n — число считается простым;
   – иначе генерируется новое число.
4. Готовые простые записываются в тестовый набор или используются для моделирования нагрузки.

В коде:

# Проверка простоты через перебор делителей
def is_prime(n):
    if n < 2:
        return False
    i = 2
    while i * i <= n:
        if n % i == 0:
            return False
        i += 1
    return True

# Генерация набора простых чисел для тестовых данных
def generate_primes(limit, count):
    primes = []
    while len(primes) < count:
        num = random.randint(2, limit)
        if is_prime(num):
            primes.append(num)
    return primes

Решето Эратосфена

Алгоритм Решето Эратосфена — классический метод для нахождения всех простых чисел вплоть до заданного числа n. Алгоритм удобен тем, что легко реализуется и быстро находит все простые числа до n — без сложных конструкций, используя только массив и последовательные проходы по нему.

Он хорошо работает в задачах, где нужно заранее подготовить таблицу простых чисел: от факторизации и анализа числовых последовательностей до базовых криптографических процедур. Подходит в тех случаях, когда верхняя граница n достаточно мала, чтобы разместить массив в памяти; для больших значений используют его сегментированные версии.

Как работает алгоритм

1. Запишем все целые числа от 2 до n включительно.
2. Начинаем с p = 2 — первое простое число.
3. Зачёркиваем (отмечаем как составные) все числа, кратные p: 2p, 3p, 4p, … до n.
4. Находим следующее незачёркнутое число > p и присваиваем p новое значение.
5. Повторяем шаги 3–4 до тех пор, пока p² ≤ n.
6. После этого все оставшиеся незачеркнутые числа — простые. 

Пример: ускорение криптографических операций при генерации ключей

Многие криптографические алгоритмы (например, RSA) используют простые числа. Чтобы быстро получать кандидатов на простые числа или проверять делители больших чисел, системы подготавливают таблицу всех простых чисел до некоторой границы — и делают это с помощью Решета Эратосфена.

Как используется в процессе

1. Система задает диапазон, например до 1 000 000.
2. Прогоняет Решето Эратосфена и получает список всех простых чисел.
3. Этот список дальше используется:
   – для быстрой проверки делимости при тестах простоты;
   – при подборе криптографических параметров;
   – для ускорения вероятностных алгоритмов факторизации.

В коде:

def sieve(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False

    p = 2
    while p * p <= n:
        if prime[p]:
            for i in range(p*p, n + 1, p):
                prime[i] = False
        p += 1

    return [i for i in range(n + 1) if prime[i]]

# Получаем таблицу простых для криптографических операций
precomputed_primes = sieve(1_000_000)

Графическое изображение алгоритмов

Алгоритмы могут записывать текстом, кодом, псевдокодом или графически — в виде блок-схем. Это специальные схемы, состоящие из геометрических фигур, которые описывают те или иные действия. Например, начальная и конечная точка на схеме — соответственно, начало и конец алгоритма, параллелограмм — ввод или вывод данных, ромб — условие. Простые действия обозначаются прямоугольниками, а соединяются фигуры с помощью стрелок — они показывают последовательности и циклы.

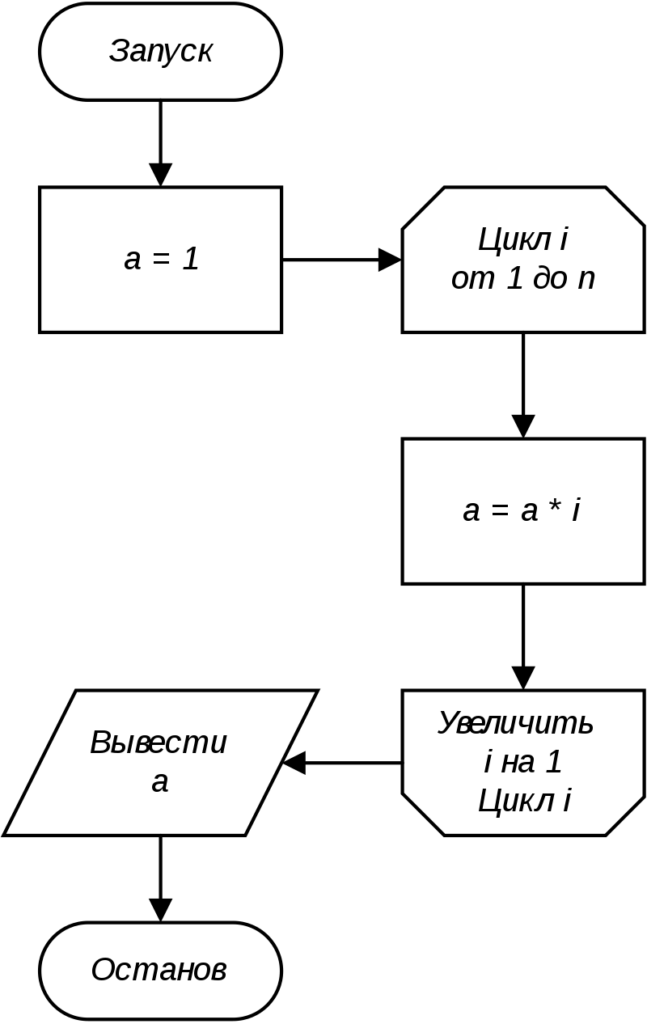
В схемах подписаны конкретные действия, условия, количество повторений циклов и другие детали. Это позволяет нагляднее воспринимать алгоритмы.

Сложность алгоритма

Понятие «сложность» — одно из ключевых в изучении алгоритмов. Оно означает не то, насколько трудно понять тот или иной метод, а ресурсы, затраченные на вычисление. Если сложность высокая, алгоритм будет выполняться медленнее и, возможно, тратить больше аппаратных ресурсов; такого желательно избегать.

Сложность обычно описывают большой буквой O. После нее в скобках указывается значение, от которого зависит время выполнения. Это обозначение из математики, которое описывает поведение разных функций.

Какой бывает сложность. Полностью разбирать математическую O-нотацию, как ее называют, мы не будем — просто перечислим основные обозначения сложности в теории алгоритмов.

•  O(1) означает, что алгоритм выполняется за фиксированное константное время. Это самые эффективные алгоритмы.
•  O(n) — это сложность линейных алгоритмов. n здесь и дальше обозначает размер входных данных: чем больше n, тем дольше выполняется алгоритм.
•  O(n²) тоже означает, что чем больше n, тем выше сложность. Но зависимость тут не линейная, а квадратичная, то есть скорость возрастает намного быстрее. Это неэффективные алгоритмы, например с вложенными циклами.
•  O(log n) — более эффективный алгоритм. Скорость его выполнения рассчитывается логарифмически, то есть зависит от логарифма n.
•  O(√n) — алгоритм, скорость которого зависит от квадратного корня из n. Он менее эффективен, чем логарифмический, но эффективнее линейного.

Существуют также O(n³), O(nn) и другие малоэффективные алгоритмы с высокими степенями. Их сложность растет очень быстро, и их лучше не использовать.

Графическое описание сложности. Лучше разобраться в сложности в O-нотации поможет график. Он показывает, как изменяется время выполнения алгоритма в зависимости от размера входных данных. Чем более пологую линию дает график, тем эффективнее алгоритм.

O-нотацию используют, чтобы оценить, эффективно ли использовать ту или иную последовательность действий. Если данные большие или их много, стараются искать более эффективные алгоритмы, чтобы ускорить работу программы.

Использование алгоритмов в IT

Мы приведем несколько примеров использования разных алгоритмов в отраслях программирования. На самом деле их намного больше — мы взяли только часть, чтобы помочь вам понять практическую значимость алгоритмов.

Разработка ПО и сайтов. Алгоритмы используются для парсинга, то есть «разбора» структур с данными, таких как JSON. Парсинг — одна из базовых задач, например в вебе. Также алгоритмы нужны при отрисовке динамических структур, выводе оповещений, настройке поведения приложения и многом другом.

Работа с данными. Очень активно алгоритмы применяются при работе с базами данных, файлами, где хранится информация, структурами вроде массивов или списков. Данных может быть очень много, и выбор правильного алгоритма позволяет ускорить работу с ними. Алгоритмы решают задачи сортировки, изменения и удаления нужных элементов, добавления новых данных. С их помощью наполняют и проходят по таким структурам, как деревья и графы. 

Отдельное значение алгоритмы имеют в Big Data и анализе данных: там они позволяют обработать огромное количество информации, в том числе сырой, и не потратить на это слишком много ресурсов.

Поисковые задачи. Алгоритмы поиска — отдельная сложная отрасль. Их выделяют в отдельную группу, в которой сейчас десятки разных алгоритмов. Поиск важен в науке о данных, в методах искусственного интеллекта, в аналитике и многом другом. Самый очевидный пример — поисковые системы вроде Google или Яндекса. Кстати, подробности об используемых алгоритмах поисковики обычно держат в секрете.

Машинное обучение. В машинном обучении и искусственном интеллекте подход к алгоритмам немного другой. Если обычная программа действует по заданному порядку действий, то «умная машина» — нейросеть или обученная модель — формирует алгоритм для себя сама в ходе обучения. Разработчик же описывает модель и обучает ее: задает ей начальные данные и показывает примеры того, как должен выглядеть конечный результат. В ходе обучения модель сама продумывает для себя алгоритм достижения этого результата.

Такие ИИ-алгоритмы могут быть еще мощнее обычных и используются для решения задач, которые разработчик не в силах разбить на простые действия сознательно. Например, для распознавания предметов нужно задействовать огромное количество процессов в нервной системе: человек просто физически не способен описать их все, чтобы повторить программно.

В ходе создания и обучения модели разработчик тоже может задействовать алгоритмы. Например, алгоритм распространения ошибки позволяет обучать нейросети. 

Алгоритмы: коротко о главном

Итак, что можно считать алгоритмом?

Алгоритм — это четкая последовательность шагов, выполнение которых даёт заранее известный результат. Он представляет собой набор инструкций для решения конкретной задачи, часто используемый в информатике и программировании.

Ключевые свойства алгоритмов:

• дискретность — алгоритм состоит из отдельных шагов, выполняемых поочерёдно;
• результативность — алгоритм должен обязательно приводить к результату и не оставлять состояние неопределённости;
• детерминированность — каждый шаг описан однозначно и не допускает неоднозначности;
• массовость — алгоритм применим к множеству входных данных, не зависит от конкретного случая;
• конечность — выполнение должно завершаться за конечное число шагов.

Среди основных видов алгоритмов выделяют:

• линейные алгоритмы — последовательное выполнение шагов без ветвлений или повторений;
• ветвящиеся алгоритмы — включают условия, по которым выбирается один из путей выполнения;
• циклические алгоритмы — предусматривают повторение блока действий до выполнения условия выхода;
• рекурсивные алгоритмы — вызывают сами себя с другими входными данными;
• вероятностные алгоритмы — результат или путь выполнения зависит также от случайных величин. 

Алгоритмы применяются во всех направлениях IT: разработке программного обеспечения, работе с данными и базами, поисковых системах, машинном обучении и анализе больших массивов информации.