Бинарный поиск — тип поискового алгоритма, который последовательно делит пополам заранее отсортированный массив данных, чтобы обнаружить нужный элемент. Другие его названия — двоичный поиск, метод половинного деления, дихотомия.
Принцип работы алгоритма бинарного поиска
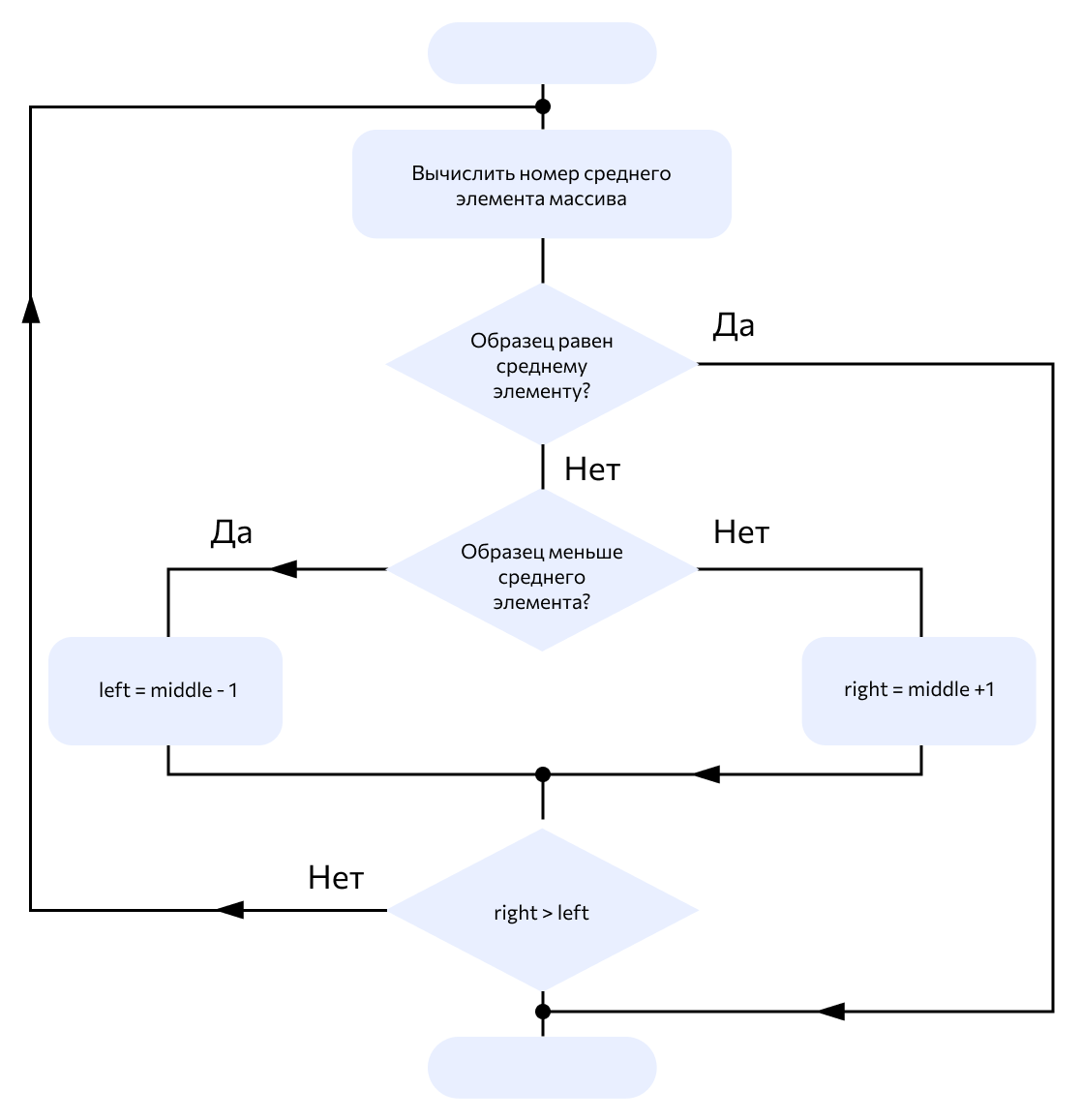
Основная последовательность действий алгоритма выглядит так:
- Сортируем массив данных.
- Делим его пополам и находим середину.
- Сравниваем срединный элемент с заданным искомым элементом.
- Если искомое число больше среднего — продолжаем поиск в правой части массива (если он отсортирован по возрастанию): делим ее пополам, повторяя пункт 3. Если же заданное число меньше — алгоритм продолжит поиск в левой части массива, снова возвращаясь к пункту 3.
Реализация бинарного поиска
Существуют два способа реализации бинарного поиска.
1. Итерационный метод. При таком подходе используется цикл, тело которого повторяется, пока не найдется заданный элемент либо не будет установлено, что его нет в массиве. Например, в Python для этой цели удобно использовать цикл while.
2. Рекурсивный подход. В этом случае пишется функция, которая вызывает сама себя (рекурсивно), пока не будет найден искомый элемент в массиве.
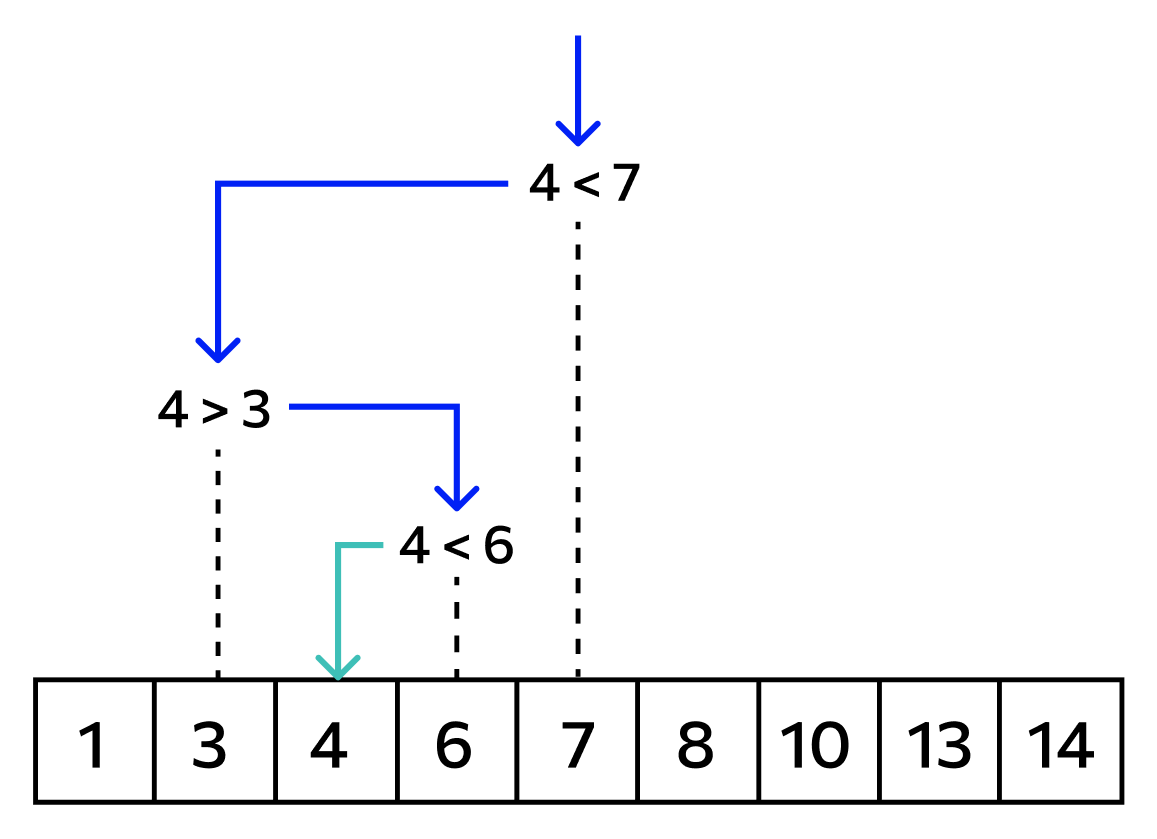
Приведем примеры реализации этих методов на Python.
Пусть есть массив чисел [5, 8, 9, 1, 23, 7, 3, 0, 15], и необходимо найти позицию числа 5 в упорядоченном списке. На вход такой функции необходимо подать уже отсортированный массив, для этого воспользуемся встроенным методом sorted(), который упорядочивает массив данных по возрастанию.
Код, использующий итерационный подход, будет выглядеть так:
def findPosition(num_list, number):
first = 0
last = len(num_list) - 1
while first <= last:
middle = first + (last - first) // 2
if num_list[middle] == number:
return middle
elif num_list[middle] < number:
first = middle + 1
else:
last = middle - 1
return -1
num_list = sorted([5, 8, 9, 1, 23, 7, 3, 0, 15])
number = 5
print(findPosition(num_list, number))При использовании рекурсивного поиска код на Python можно написать так:
def findPosition(num_list, number, first, last):
if last >= first:
middle = first + (last - first) // 2
if num_list[middle] == number:
return middle
elif num_list[middle] < number:
return findPosition(num_list, number, middle + 1, last)
else:
return findPosition(num_list, number, first, middle - 1)
else:
return -1
num_list = sorted([5, 8, 9, 1, 23, 7, 3, 0, 15])
number = 5
print(findPosition(num_list, number, 0, len(num_list) - 1))В некоторых языках программирования, включая Python, есть готовые функции для выполнения бинарного поиска. Модуль бинарного поиска называется bisect. Проиллюстрируем его работу на примере:
from bisect import bisect_left
def findPosition(num_list, number):
pos = bisect_left(num_list, number)
if pos < len(num_list):
return pos
return False
num_list = sorted([5, 8, 9, 1, 23, 7, 3, 0, 15])
number = 5
print(findPosition(num_list, number))В каких случаях используют бинарный поиск
Двоичный поиск подходит для нахождения позиций элемента в упорядоченном списке: в этом случае он эффективнее линейного, поскольку массив данных на каждом шаге разделяется надвое и одна половина сразу отбрасывается. Последовательная сложность двоичного метода в худшем и среднем случаях равна O(log n), в лучшем — O(1) (если обнаруживаем искомый элемент на первой итерации). Для сравнения: вычислительная сложность линейного поиска равна O(n) (обычный проход по всем элементам в поисках нужного).
У бинарного поиска есть недостаток — он требует упорядочивания данных по возрастанию. Сложность сортировки — не менее O(n log n). Поэтому, если список короткий, используется все-таки линейный поиск.
Разновидности алгоритма
На основе бинарного поиска разработано несколько дополнительных разновидностей поисковых алгоритмов:
- однородный бинарный поиск, при котором аргумент поиска А сравнивается с ключом Ki, где i — золотое сечение интервала (оно выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка);
- троичный поиск, когда интервал делится на три части вместо двух. Обычно применяется для поиска положения экстремума функции;
- интерполирующий поиск, который предсказывает позицию нужного элемента на основе разницы значений. Эффективен, если элементы распределены достаточно равномерно;
- дробный спуск — применяется для ускорения двоичного поиска в многомерных массивах данных, и другие.








0 комментариев