Линейная регрессия (Linear regression) — это это математическая модель, которая описывает связь нескольких переменных. Модели линейной регрессии представляют собой статистическую процедуру, помогающую прогнозировать будущее. Она применяется в научных сферах и в бизнесе, а в последние десятилетия используется в машинном обучении.
Для чего нужна линейная регрессия
Задача регрессии в машинном обучении — это предсказание одного параметра (Y) по известному параметру X, где X — набор параметров, характеризующий наблюдение.
Как работает линейная регрессия
Возьмем небольшой набор данных. Предположим, что это группа коттеджей, расположенных в одном районе. На оси Х обозначена их площадь, а на оси Y — рыночная стоимость. Чтобы увидеть, как стоимость дома зависит от его площади, построим регрессию.
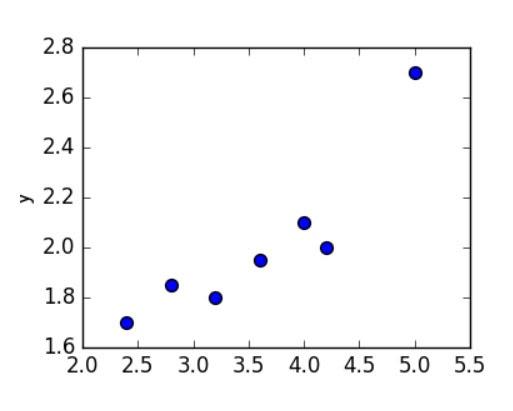
Это будет простая линейная регрессия с одной переменной. Изменится площадь дома — изменится и стоимость. Для вычисления используем стандартное уравнение регрессии: f (x) = b + m⋅x, где m — это наклон линии, а b — ее сдвиг по оси Y. То есть изменение коэффициентов m и b будет влиять на расположение прямой:
- если изменить m — прямая наклонится сильнее влево или вправо;
- если изменить b — прямая сместится вверх или вниз по оси Y.
Провести прямую линию через все точки на графике не получится, если они расположены в хаотичном порядке. Поэтому с помощью линейной регрессии определяется оптимальный вариант расположения этой прямой. Некоторые точки все равно останутся на расстоянии, но оно должно быть минимальным. Расчет этого минимального расстояния от прямой до каждой точки называется функцией потерь.
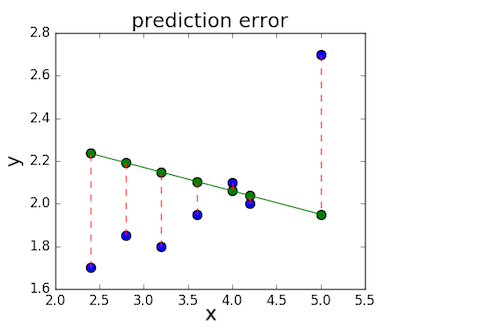
Для оценки точности регрессии используют разные метрики, например MSE (от англ. mean squared error — средняя квадратическая ошибка). Чем ниже MSE, тем лучше модель.
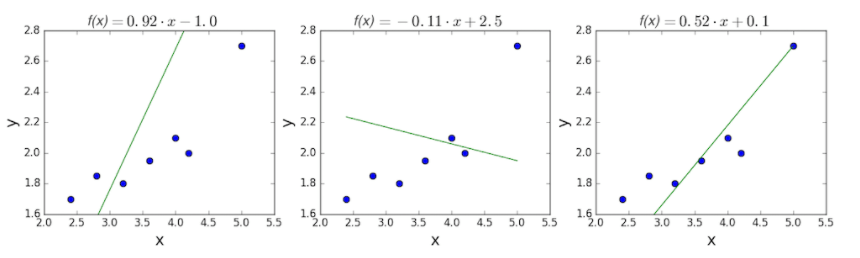
В первом случае MSE будет равна 0,17, во втором — 0,08, а в третьем — 0,02. Получается, что третья прямая лучше всего показывает зависимость цены дома от его площади.
Расчет линейной регрессии в Python
Построим регрессию, чтобы узнать, как кассовые сборы фильма зависят от бюджета, который вложили в его производство.
В открытом доступе есть информация о каждом фильме, вышедшем в прокат. Например, самый кассовый фильм планеты «Аватар» собрал в прокате $2 743 577 587 при затратах $237 000 000, то есть окупился больше чем 10 раз. Культовый фильм «Карты, деньги, два ствола» собрал кассу $28 300 000 при бюджете всего $1 350 000, то есть окупился 20 раз. При этом сборы второго фильма не дотягивают даже до бюджета первого. Как на основе этих данных выбрать оптимальный бюджет?
Для расчета понадобится csv-файл, который содержит информацию о бюджетах и сборах 5 034 фильмов, которые когда-то выходили в прокат. Эти данные станут базой для исследования.
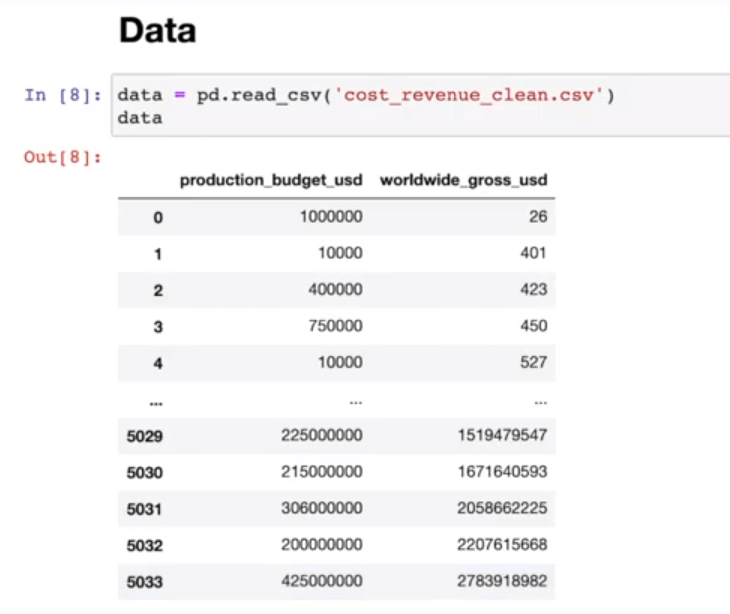
Построим модель линейной регрессии с помощью Python. Для этого нужно импортировать несколько библиотек:
- pandas поможет прочитать данные;
- matplotlib будет отвечать за визуализацию результата;
- sklearn поможет создать саму модель линейной регрессии.
Модель линейной регрессии, которую нужно будет обучить, импортируется с помощью библиотеки sklearn. В качестве X будет колонка production_budget_usd, а в качестве Y – колонка worldwide_gross_usd.
На основе этих данных определяется нужный наклон прямой и расположение относительно осей координат. Это и будет нужной линейной регрессией, по которой можно предсказать сборы собственного фильма, выбрав подходящий бюджет.
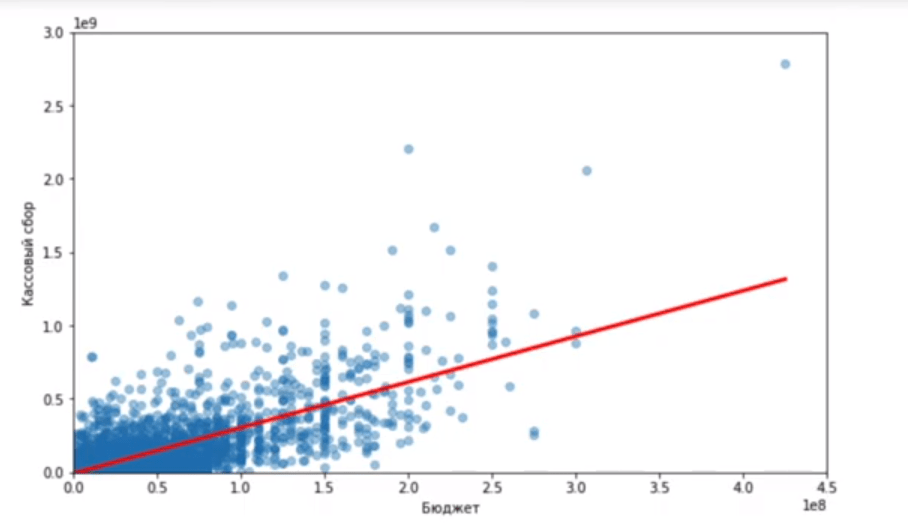
В итоге получится график того, как соотносятся бюджеты и кассы у фильмов в списке. Каждая точка — это отдельная кинолента. На оси Х показаны затраты на производство, а на оси У — сколько она заработала. Теперь через эти точки нужно провести прямую так, чтобы она была максимально близка ко всем точкам на графике.
Множественная линейная регрессия
В жизни кассовые сборы кино зависят не от одной переменной, а от совокупности разных факторов: популярности жанра, режиссера, каста актеров и затрат на промокампанию. Если рассчитать все факторы, влияющие на сборы, то уравнение изменится:
Было f (x) = b + m⋅x
Стало f(x) = b + m1*x1 + … + mn*xn
Каждый коэффициент в нем показывает важность признаков. То есть множественная регрессия демонстрирует, как каждый параметр влияет на расположение прямой, и выбирает оптимальный вариант точно так же, как и линейная — с помощью функции потерь.








0 комментариев