Логистическая регрессия

Логистическая регрессия — это статистический тест, который нужен, чтобы предсказать вероятность какого-то события. Для этого используются данные о событиях, которые уже случались.

Задача регрессии — это прогнозирование. На основе логистической регрессии построен регрессионный анализ данных и некоторые методы машинного обучения. Алгоритмы, основанные на регрессии, занимаются прогнозами. Конкретно логистическая регрессия предсказывает вероятности, чаще всего — для величин, принимающих только два значения.

Например, алгоритм может взять данные о посещениях сайта по месяцам и посчитать вероятность, что в следующем месяце сайт посетят более N раз.

Что такое логистическая регрессия и как она работает

Самый простой для понимания тип логистической регрессии — бинарная. Она прогнозирует какую-то бинарную величину, то есть принимающую только два значения. Величина, которую прогнозируют, называется зависимой переменной. А факторы, на основе которых ее предсказывают, называются независимыми переменными, или предикторами.

Пример — кредитный скоринг. Есть много независимых факторов: возраст человека, уровень дохода, профессия. И зависимая переменная: дадут человеку кредит или нет. Она основана на предикторах и принимает только два значения: «дадут» или «не дадут».

Бинарная логистическая регрессия — это способ предсказать, с какой вероятностью зависимая переменная примет одно из двух значений. Еще бывает множественная логистическая регрессия, она сложнее и может использоваться для переменных с большим количеством значений.

В примере выше бинарная логистическая регрессия поможет понять, с какой вероятностью человеку дадут кредит, если известны нужные независимые факторы.

Разделение значений

Чтобы понять, как это работает, нужно немного углубиться в статистику. Есть такая задача — бинарная классификация. Это разделение множества значений на два больших взаимоисключающих класса. 

Например, множество «шахматные фигурки» можно разделить на классы «белые» и «черные».

В сказке Золушка отделяет чечевицу от гороха — решает задачу бинарной классификации

Линейный дискриминант

Бинарную классификацию можно визуализировать на графике. Значения будут точками, которые образуют два «облака», отделенных друг от друга. Их условно называют классами «+» и «-». 

Между облаками можно провести плоскость — разделить их прямой стеной. Обычно график трехмерный, иногда используют четырехмерный, если ровную стену провести не получается.

Эта «стена» называется линейным дискриминантом. Он линейный, потому что плоскость ровная. А слово «дискриминант» означает «разделитель».

Класс «+» называется так, потому что там координаты точек больше, чем координаты расположения дискриминанта. В классе «-» всё, соответственно, наоборот.

В геометрии любой фигуре соответствует какая-то функция, которая ее описывает. По функции можно нарисовать фигуру. У линейного дискриминанта тоже есть своя функция, которая показывает, где именно проходит граница между двумя большими «группами».

С помощью функции линейного дискриминанта можно проверить, насколько далеко или близко та или иная точка находится от «стены». Для этого нужно подставить координаты точки в формулу, по которой считается плоскость. Получится число:

• если оно положительное — точка находится со стороны класса «+»;
• если отрицательное — точка находится со стороны класса «-»;
• если равно нулю — точка лежит прямо на границе.

Назовем это число t. Чем больше оно по модулю, тем дальше точка от границы. А значит — тем выше вероятность, что она принадлежит к тому классу, со стороны которого находится. Если точка лежит на границе, то вероятность принадлежности к каждой группе — 0,5.

Отношение шансов

Но число t, которое мы получили — совсем не вероятность. Оно говорит только об области и расстоянии до границы. А чтобы преобразовать это значение в вероятность, используется функция отношения шансов.

Отношение шансов можно посчитать по найденному значению. Это экспонента в степени t: et.

А из отношения шансов можно «вытащить» вероятность. Формула такая:

P+ = et1 + et

P+ — число от 0 до 1, вероятность того, что значение принадлежит классу «+». Это то, что мы искали. Так работает логистическая регрессия.

Кто и зачем пользуется логистической регрессией

Вообще логистическая регрессия пришла из статистики. Ею пользовались ученые, математики, инженеры — все, кому нужно было заниматься статистическими предсказаниями, например прогнозировать вероятные результаты эксперимента.

Сейчас сфер применения намного больше:

• машинное обучение — ML-инженеры пользуются логистической регрессией для задач предсказания и классификации. Обычно задачки на обучение с учителем, использующие регрессию, одни из первых в курсах по ML;
• нейронные сети — это ответвление ML с глубоким обучением. Нейросети состоят из искусственных нейронов, которые при работе пользуются логистической регрессией;
• анализ данных — регрессия позволяет предсказать какое-то событие на основе информации;
• бизнес-аналитика — с помощью регрессии можно, например, предсказать, купит человек товар или нет.

Медицина с помощью регрессии может предсказать вероятность какого-нибудь заболевания. Финансовая сфера — оценить платежеспособность: скоринг действительно работает именно так.

Чем логистическая регрессия отличается от линейной

Два основных метода регрессии — логистическая и линейная. Хотя названия похожи, это разные вещи.

Сходства. Линейная и логистическая регрессии похожи тем, что обе занимаются предсказаниями и пользуются при этом линейными уравнениями. Обе обычно используются для прогнозирования и иногда для классификации. Обе применяются в машинном обучении и анализе данных.

Различия. Главное различие — результат прогноза. Линейная регрессия показывает предполагаемое значение зависимой величины. А логистическая регрессия — вероятность, что величина примет одно из двух бинарных значений.

Различия хорошо видно на графике.

• График линейной регрессии — прямая линия, которая может принимать разные значения.
• График логистической регрессии — кривая, которую описывает сигмоидная функция. Ее еще называют s-curve, логистической или логит-функцией. Она принимает значения от 0 до 1.

А еще каждый вид регрессии используется «в связке» с некоторыми другими действиями: например, функцией для минимизации ошибки. Набор этих действий для линейной и логистической регрессий — разный. Линейная минимизирует ошибки с помощью метода наименьших квадратов, а логистическая — с помощью метода максимального правдоподобия.

Что нужно, чтобы посчитать регрессию

Данные. Нужен такой набор данных:

• зависимая бинарная переменная;
• несколько независимых переменных, или предикторов;
• набор значений, которые принимали независимые переменные — и значений, которые при таких условиях принимала зависимая.

Независимые переменные могут тоже быть бинарными, могут быть категориальными или интервальными. У категориальных переменных есть несколько «категорий» ответов, скажем: «в браке», «в разводе», «не женат(а)». Значения интервальных, или непрерывных переменных — числа, например атмосферное давление или курс валюты.

Условия. Чтобы данные можно было использовать, должно выполняться несколько требований. Если они не выполняются, результат регрессии будет искажен:

• зависимость между предикторами и результатами должна быть линейной (чем больше одно — тем больше или меньше другое, без колебаний);
• предикторы должны не зависеть друг от друга или от одного и того же внешнего фактора;
• значения независимых переменных должны меняться в разных наблюдениях — если переменная будет неизменной все время, не получится оценить ее влияние;
• сами наблюдения, по которым собирались данные, должны не зависеть друг от друга;
• данные должны быть гомоскедастичными — это значит, что их разброс относительно линейного графика должен быть примерно одинаковым на всей его длине.

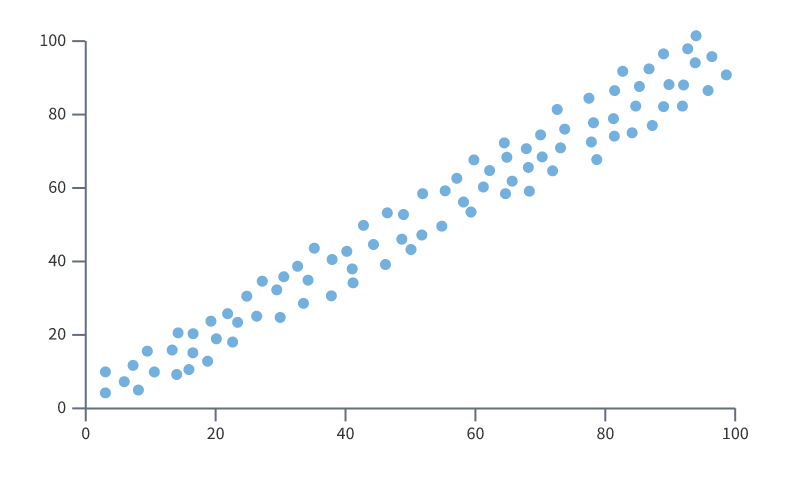
Так гомоскедастичность выглядит визуально — дисперсия данных примерно одинаковая на протяжении всего графика

Вспомогательные процедуры. Например, бывает нужно отфильтровать входные данные от «шумов» и повторов, сгруппировать их, проверить на отсутствие коллинеарности. То есть — проверить, не связаны ли разные предикторы друг с другом. По условию входные переменные должны быть независимы один от другого. Словом, нужно проверить, что выполняются требования к входным данным.

Инструменты для анализа с помощью логистической регрессии

Чтобы собрать, посчитать и интерпретировать данные, нужно понимать, как работает этот метод. Но это не значит, что рассчитывать все значения придется вручную. Ручные расчеты — долгие, неэффективные, в них высок риск человеческой ошибки.

Поэтому расчеты, вывод значения и визуализацию автоматизируют. Для этого аналитики и инженеры пользуются языками программирования и специальным ПО.

Самый знакомый пользователю вариант — Excel. В офисной программе множество функций и формул, она умеет высчитывать значения для больших объемов данных, сводить их в таблицы, объединять и разделять. Там есть все инструменты для многих типов анализа. Можно и рисовать графики на основе данных в таблице.

Можно реализовать регрессию с помощью языка Python. Его традиционно применяют в науке о данных и в машинном обучении: он гибкий и удобный, его легко приспособить под такие задачи. Есть библиотеки и фреймворки, где собраны методы для анализа, например Anaconda.

Еще можно писать на языке R. Это специализированный язык программирования, которым пользуются аналитики, математики, дата-саентисты и другие подобные специалисты. Он специально разработан для решения задач статистики и анализа.

Для аналитики есть специализированное ПО. Его можно использовать для разных видов анализа, но обычно покупают для корпоративных задач — оно платное и недешевое. Как пример — Power BI.

Как научиться логистической регрессии

Понять основы логистической регрессии можно в теории, а вот чтобы их применять — нужна практика. Можете начать с учебников и упражнений в открытом доступе, параллельно изучать другие функции, которые относятся к классу регрессий. Мы советуем практиковаться с самого начала: необязательно считать вручную, можно писать код на Python или подсчитывать значения в Excel. Но практика нужна, чтобы лучше понять тему.