Временной ряд

Временной ряд — последовательность значений, которые протекают и измеряются в определенном временном промежутке. Основная характеристика, которая отличает временной ряд от простой выборки данных – указанное время измерения или номер изменения по порядку.

Пример временного ряда: биржевой курс
Пример выборки данных: электронные почты клиентов магазина

Временные ряды используются для аналитики и прогнозирования, когда важно определить, что будет происходить с показателями в ближайший час/день/месяц или год: например, сколько пользователей скачают за день мобильное приложение. Показатели для составления временных рядов могут быть не только техническими, но и экономическими, социальными и даже природными.

Временные ряды и их характеристики

Временная последовательность данных – дополнительный источник информации. Предполагается, что временные ряды генерируются регулярно, но на практике это не всегда так. Регулярный компонент временного ряда – систематическая составляющая, которая имеет определенную прогнозируемую характеристику. В нерегулярных рядах измерения проходят не через регулярный интервал времени. Пополнение банковской карты – пример нерегулярных временных рядов.

Помимо регулярности временные ряды делятся на детерминированные и недетерминированные.

Детерминированный временной ряд – ряд, в котором нет случайных аспектов или показателей: он может быть выражен формулой. Это значит, что мы можем проанализировать, как показатели вели себя в прошлом и прогнозировать их поведение в будущем.

Недетерминированный временной ряд имеет случайный аспект и прогнозирование будущих действий становится сложнее. Природа таких показателей случайна и анализ происходит благодаря средним значениям и дисперсии.

Стационарные и нестационарные ряды

На наблюдение за показателями и их систематизацией влияют тенденции и сезонные эффекты. От этих условий зависит сложность моделирования системы прогнозирования. Временные ряды делятся по наличию или отсутствию тенденций и сезонных эффектов на стационарные и нестационарные.

В стационарных временных рядах статистические свойства не зависят от времени, поэтому результат легко предсказать. Большинство статистических методов предполагают, что все временные ряды должны быть стационарными. Пример стационарных временных рядов – рождаемость в России. Конечно, она зависит от множества факторов, но ее спад или рост возможно предсказать: у рождаемости нет ярко выраженной сезонности.

В нестационарных временных рядах статистические свойства меняются со временем. Они показывают сезонные эффекты, тренды и другие структуры, которые зависят от временного показателя. Пример – международные перелеты авиакомпаний. Количество пассажиров в те или иные направления меняются в зависимости от сезонности.

Для классических статистических методов удобнее создавать модели стационарных временных рядов. Если у нас прослеживается четкая тенденция или сезонность во временных рядах, то нам следует смоделировать эти компоненты и удалить их из наблюдений. Из наблюдений удаляют «шум» – дополнительный компонент, который мешает усреднению данных. Машинное обучение позволяет эффективно работать с моделями нестационарных рядов.

Прогнозирование временных рядов — популярная аналитическая задача, которую используют в разных сферах жизни – бизнес, наука, исследования общества и потребительского поведения. Прогнозы используются для предсказания, например, сколько серверов понадобится онлайн-магазину, когда спрос на товар вырастет. Ниже мы расскажем о нескольких моделях прогнозирования.

PACF и ACF

Функция автокорреляции и функция частичной автокорреляции необходимы для определения правильных параметров модели ARIMA. Оба являются измерениями линейной памяти стационарного процесса. Они вычисляют корреляцию наблюдения со значениями запаздывания.

Модели ARMA и ARIMA

Они сыграли фундаментальную роль в обработке сигналов связи во время Второй мировой войны. После их начали использовать в анализе временных рядов в 1970 году.

ARMA (Autoregressive Moving Average) – авторегрессионная модель скользящей средней

ARIMA (Autoregressive Integrated Moving Average) – авторегрессионная интегрированная модель скользящей средней

AR → Авторегрессионная модель

Интересующая переменная представляет собой линейную регрессию прошлых значений самой переменной, которая подразумевает, что будущее зависит от прошлого. Модель линейной регрессии состоит из наблюдений интересующей переменной с лагом, который улавливает все, что не объясняется регрессией.

I → Интегрированный

Это относится к различным методам вычисления различий между последовательными наблюдениями для получения стационарного процесса из нестационарного процесса. Он определяется параметром d, который показывает, сколько раз наблюдаются различия.

MA → Модель скользящей средней

Это регрессионная модель, которая использует прошлые ошибки прогноза для прогнозирования интересующей переменной. Скользящая средняя имеет порядок q, она определяет размер окна скользящей средней.

Для работы с временными рядами с сезонными компонентами используется SARIMA (интегрированное скользящее среднее сезонной авторегрессии). Это расширение модели ARIMA, добавляющее в ARIMA сезонные условия.

Prophet

Prophet разработан командой Facebook Core Data Science^* и представляет собой инструмент с открытым исходным кодом для бизнес-прогнозирования. Модель Prophet основана на трех переменных:

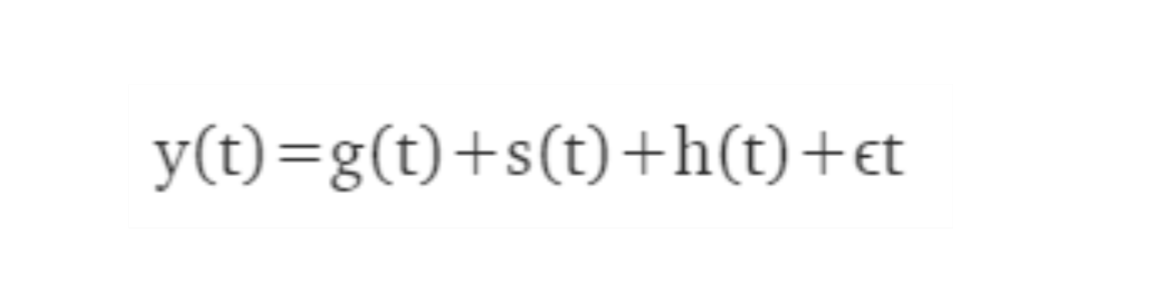
g (t) – тренд. Логистическая функция позволяет моделировать рост с насыщением, когда при увеличении показателя снижается темп его роста.

s (t) – сезонность отвечает за моделирование периодических изменений, связанных с недельной и годовой сезонностью.

h (t) – праздники и события. Учитываются аномальные дни, которые не влияют на сезонность.

ε(t) — ошибка. Содержит информацию, которую модель не учитывает.

У Prophet существует больше инструментов для обработки и сортировки данных по сезонности, чем у SARIMA. Такое преимущество позволяет анализировать временные ряды с различной сезонностью – неделей, месяцем кварталом или годом.

Прогноз по методу экспоненциального сглаживания.

Преимущество этого метода – возможность сделать прогноз на длительный период. Математически экспоненциальное сглаживание выражается так:

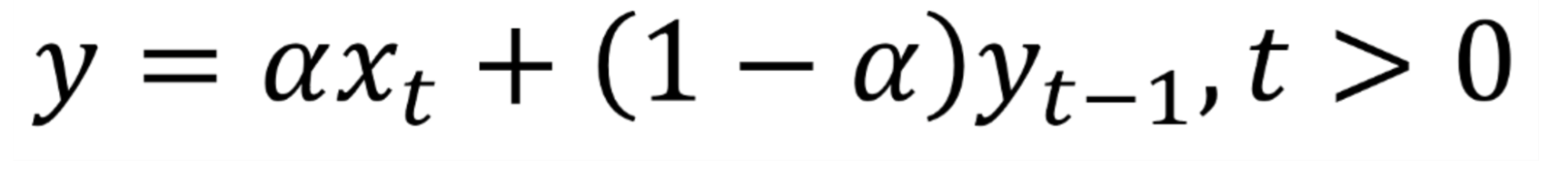
a (alfa) – коэффициент сглаживания, который принимает значения от 0 до 1. Он определяет, насколько продолжительность изменит существующие значения в базе данных.

x – текущее значение временного ряда (например, объем продаж)

y – сглаженная величина на текущий период

t – значение тренда за предыдущий период.

Пример экспоненциального сглаживания:

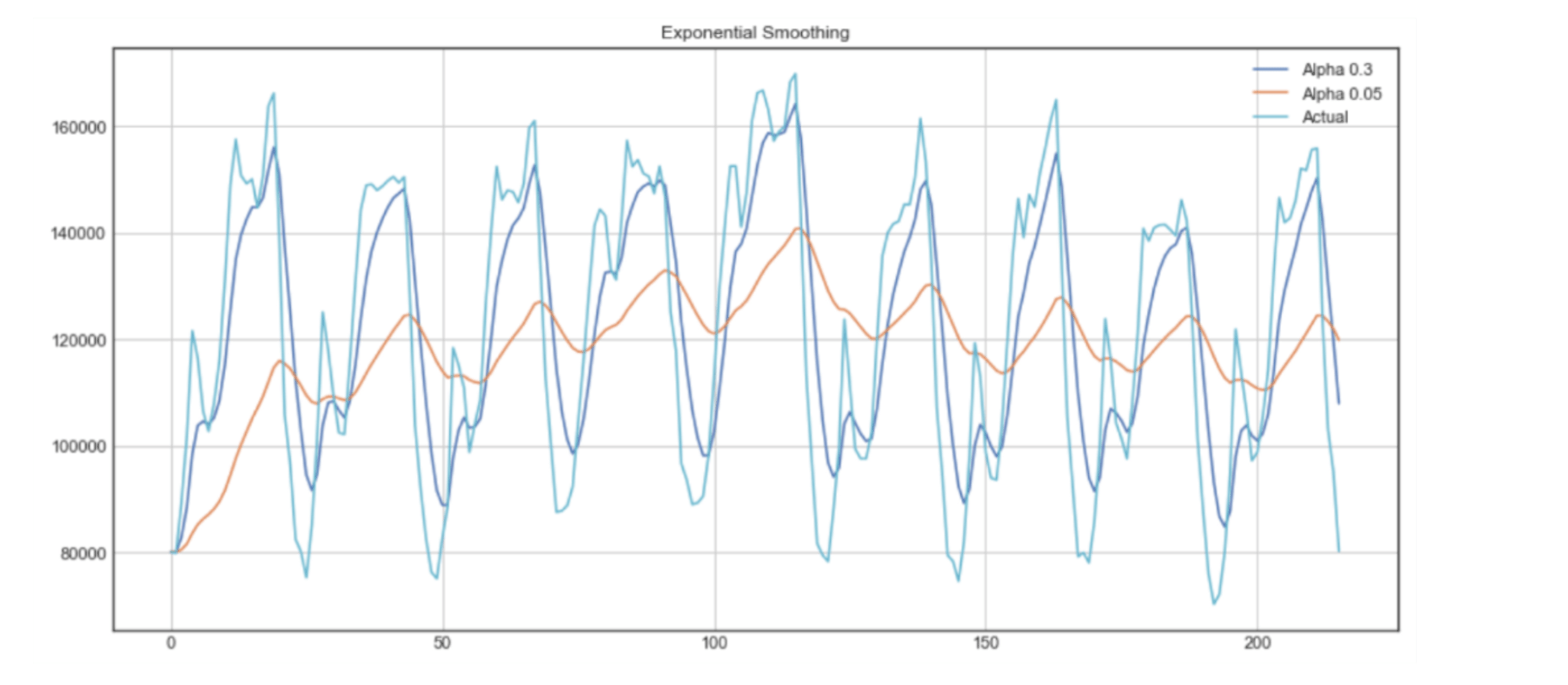
На графике темно-синяя линия представляет экспоненциальное сглаживание временного ряда с коэффициентом сглаживания 0,3, а оранжевая линия использует коэффициент сглаживания 0,05.

Как можно заметить, чем меньше коэффициент сглаживания, тем более плавным будет временной ряд. Это значит, что, когда коэффициент сглаживания приближается к 0, мы подходим к модели скользящего среднего.

Примеры использования термина

  Биржевой курс доллара – это временной ряд

  Из показателей температуры воздуха мы не можем составить временной ряд

* Принадлежит компании Meta, деятельность которой признана экстремистской в России.