Владеть основными методами машинного обучения и уметь интерпретировать результаты построенных моделей — must have для дата-сайентиста. Но чтобы решать нестандартные задачи, важно понимать законы математики и статистики «под капотом». Разбираемся, как именно математика помогает дата-сайентистам и какие разделы нужно знать.
Что из математики нужно для Data Science
Со знаниями математики нейронные сети и машинное обучение перестанут быть магией, вы будете понимать, как это работает. С ее помощью можно корректно обработать данные и правильно обучить модель — алгоритм, который находит оптимальное решение задачи.
Математика для Data Science нужна и если вы хотите быть в курсе последних событий в отрасли и читать научные статьи.
Самые важные разделы математики для Data Science — это:
- линейная алгебра;
- теория вероятностей и математическая статистика;
- математический анализ и методы оптимизации;
- временные ряды.
Линейная алгебра
Большой раздел математики, имеющий дело со скалярами, наборами скаляров (векторами), массивами чисел (матрицами) и наборами матриц (тензорами).
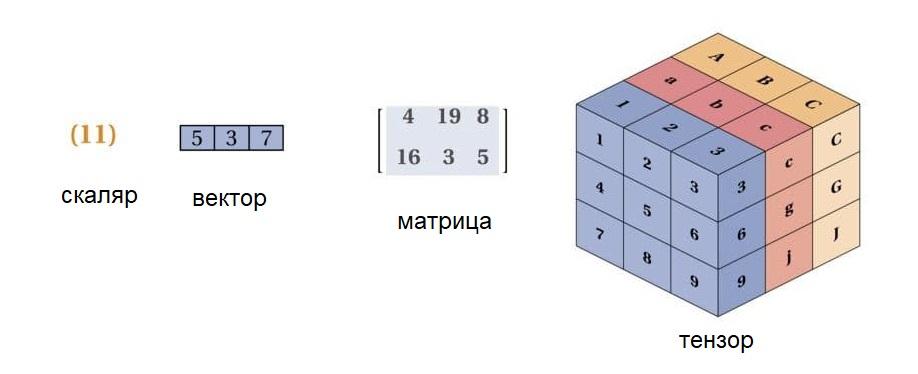
Почти любая информация может быть представлена с помощью матрицы. Объясним на примере: МРТ-снимок головного мозга — это набор плоских снимков, слоев мозга. Каждый плоский снимок можно представить как таблицу интенсивности серого цвета, а весь МРТ-снимок — это будет тензор. Затем можно найти спектр матрицы — набор всех собственных чисел векторов. С помощью спектров можно классифицировать данные на норму и патологию и выявить, например, есть ли у человека заболевание мозга.
Теперь возьмем задачу, связанную с бизнесом, — проанализировать и спрогнозировать прибыль сети магазинов. Отдельный магазин можно описать набором чисел, которые показывают размер прибыли, количество товара, количество рабочих часов в неделе, время открытия и закрытия. Набор этих чисел будет вектором. Для всей сети магазинов набор векторов составит таблицу с числами или матрицу.
Частично линейную алгебру используют в крупных компаниях при разработке рекомендательных систем (например, в YouTube). Знания о матрицах, их свойствах и операциях с ними помогут понять, как устроен механизм работы методов библиотеки NumPy, как считаются важные статистические величины для больших данных.
Теория вероятностей и математическая статистика
Статистические исследования — прообраз науки о данных: они тоже проводились, чтобы найти закономерности.
К примеру, нужно определить, какой из двух рекламных роликов более удачный. Для этого надо запустить рекламу с этими видео и получить результат. Предположим, на первый кликнула 1 тыс. пользователей, на второй — 1,1 тыс. Теория вероятностей и статистика помогают понять, случайность это или закономерность.
С помощью статистических методов можно выявлять корреляцию (зависимость) между переменными, например между днем недели и количеством покупок на маркетплейсе.
Чтобы рассчитать вероятности и проанализировать, какие колебания и связи являются случайными, а какие несут в себе смысл, нужны знания о случайных величинах, их характеристиках и распределении; также нужно уметь проверять статистические гипотезы.
Математический анализ и методы оптимизация
Математический анализ — раздел математики, он включает дифференциальное и интегральное исчисления.
В анализе данных он используется в основном (хотя далеко не только) для оптимизации — подбора наилучших параметров системы для минимизации или максимизации целевой функции. Практически каждый алгоритм машинного обучения нацелен на то, чтобы минимизировать ошибку оценки с учетом различных ограничений. В этом и состоит задача оптимизации.
Например, те, кто занимается транспортной оптимизацией, минимизируют время, затраты на проезд по платным автострадам, топливо, расходы на эксплуатацию транспортных средств.
Как глубоко нужно знать математику
Диплом механико-математического факультета МГУ точно не обязателен, чтобы стать дата-сайентистом. Джуниору-специалисту достаточно базовых знаний, но вот чтобы расти в профессии, придется углубиться.
Ответ на вопрос: «Как глубоко надо знать математику?» зависит от того, как много вы хотите зарабатывать и какую должность занять. Со специальным образованием начинать будет проще, но в целом проблем освоить специальность нет, главное — относиться к математике осознанно и понимать то, что вы делаете, а не зубрить.
Математика на собеседованиях в Data Science: к чему готовиться, в каком формате могут быть вопросы
На собеседованиях могут попросить как решить простую математическую задачу, так и предложить алгоритм решения какой-то прикладной рабочей проблемы — от подготовки данных до оценки результатов анализа. Также вас могут попросить пройти компьютерное тестирование на мышление и логику, время на выполнение которого будет ограничено, или же задать несколько устных вопросов.
Вопросы из разных разделов статистики можно посмотреть тут:
Примеры задач:
- Анализ тональности отзывов на один из продуктов (данных не всегда хватает, они могут быть грязными и немногочисленными).
- Написать тематический классификатор поисковых запросов (задача многоклассовой классификации).
Полезные ссылки
Книги:
- «Статистика и котики», Вл. Савельев.
- Книги по программированию и машинному обучению издательства O’Reilly (многие переведены на русский).
- Сборник задач по теоретическому машинному обучению В. Кантора и др.
- «Голая статистика», Ч. Уилан.
- «Математика с дурацкими рисунками», Орлин Б.
- «Время переменных. Математический анализ в безумном мире», Орлин Б.
- «Удовольствие от Х», С. Строгац.
- «Essentials of Statistics for The Behavioral Sciences», Frederick J. Gravetter.
- «Calculus», James Stewart.
Бесплатные курсы:
Видео и каналы:
- Канал по линейной алгебре на английском.
- Маткульт-привет!, канал доктора физико-математических наук Алексея Савватеева о математике.
Базовую математику для Data Science реально освоить, не имея опыта в этой сфере. На курсе «Математика для Data Science» вы узнаете, как знание математики и статистики работает в решении реальных задач. В курсе много практики, которая не ограничивается решением классических уравнений и абстрактных заданий.







