DFS

DFS, или Depth First Search, — поиск в глубину, позволяющий найти маршрут от точки A до точки B. Используется в графах — особых структурах, состоящих из точек-вершин и ребер-путей. DFS ищет маршрут по графу “в глубину”: на каждом шаге “уходит” все дальше.

Классический пример использования алгоритма — поиск случайного пути в лабиринте. DFS начинает работу в заданной точке, на каждом шаге проходит по лабиринту до следующего поворота и выбирает направление. Если путь оказывается тупиковым, алгоритм возвращается к предыдущему повороту и пробует новое направление. В результате рано или поздно находится нужный путь.

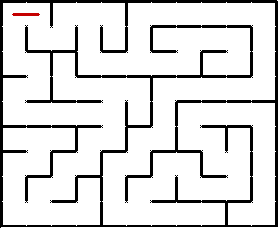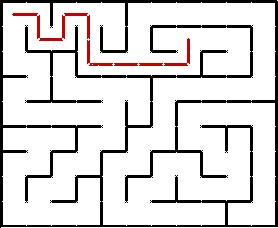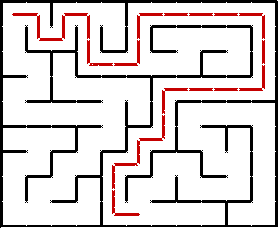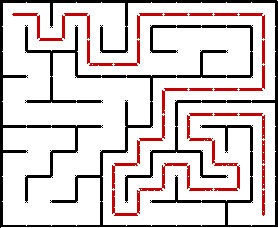
Пример использования алгоритма

DFS ищет случайный путь. Существует еще один известный алгоритм BFS, о котором у нас есть статья: тот ищет самый короткий путь.

Кроме лабиринтов, DFS может “пройти” практически по любому графу или дереву.

Кто пользуется алгоритмом

• Математики, которые работают с теорией графов для решения фундаментальных или практических задач.
• Специалисты по анализу данных и по искусственному интеллекту, так как графы часто используются в Data Science или в машинном обучении.
• Разработчики, которым бывает необходимо решать задачи поиска маршрутов, расчета потоков и другие подобные. Такие задачи могут встретиться во многих проектах: от картографического сервиса до онлайн-игры.
• Сетевые инженеры, так как в виде графов представляют компьютерные сети, а многие сетевые протоколы основаны на алгоритмах работы с графами.
• Иногда — другие специалисты, которым бывает нужно столкнуться с теорией графов. Вариации DFS используются в том числе в жизни.

Для чего нужен алгоритм DFS

• Для поиска любого маршрута в лабиринте. В отличие от алгоритма BFS, поиск в глубину ищет не самый короткий, а случайный путь. Правило прохождения лабиринта в реальной жизни “Идти с левой рукой на стене и всегда поворачивать влево” — пример DFS вне программирования.
• Для решения задач, связанных с построением маршрута: в сети, на карте, в сервисах покупки билетов и так далее. При этом непосредственно для поиска DFS используется не так часто — он чаще нужен для исследования топологии графа.
• Как составная часть расчетов в более сложных алгоритмах, например для определения максимального транспортного потока.
• Для решения ряда задач из теории графов, которые используются в программировании и математике: поиска циклов, сортировки и так далее. Мы подробно поговорим об этом ниже.

Модификации DFS

Алгоритм можно модифицировать, чтобы решить другие задачи из теории графов:

• проверить граф на двудольность. Двудольным называется граф, вершины которого можно разбить на две группы так, чтобы концы каждого ребра принадлежали вершинам из разных групп;
• найти в ориентированном графе цикл. Ориентированный граф — такой, у ребер которого есть направление. Об этом можно подробнее прочесть в нашей статье. Цикл — это замкнутый контур из вершин и ребер внутри графа: проходя по нему, в результате придешь в начальную точку;
• отсортировать и упорядочить ориентированный граф, дать вершинам номера так, чтобы ребра шли от меньшего номера к большему;
• преобразовать “синтаксическое дерево”, подвид графа, в строку;
• найти в графе определенные точки, например, так называемые мосты или шарниры.

Все эти задачи также нужны в разработке, в математике и ряде других направлений.

При чем тут рекурсия

Классическая реализация DFS — рекурсивная. Рекурсией называется процесс, когда какая-то функция вызывает себя же, но с другими аргументами. В результате одна и та же функция одновременно остается запущенной несколько раз, пока в одной из итераций не дойдет до финального решения. Тогда она вернет результат и закроется, а по каскаду закроются и все функции, приведшие к ее вызову.

С помощью рекурсии решают задачи, связанные с “глубоким” прохождением по данным. Очевидный пример — расчет чисел Фибоначчи, когда на каждом следующем шаге функция складывает два предыдущих числа. Задача DFS тоже классически решается с помощью рекурсивного алгоритма.

Но не всегда рекурсия оптимальна. Поддержка сразу нескольких запущенных одинаковых функций может отнимать много аппаратных ресурсов, поэтому существуют и нерекурсивные реализации. Их тоже нужно знать, чтобы избежать переполнения стека и других ситуаций, когда рекурсивная реализация может “упасть”.

Принцип обхода графа в глубину

Мы рассмотрим стандартный рекурсивный алгоритм обхода. О нерекурсивных реализациях поговорим ниже: их есть несколько, и у каждой свои особенности. Стандартный же принцип довольно простой для понимания, и его легко реализовать.

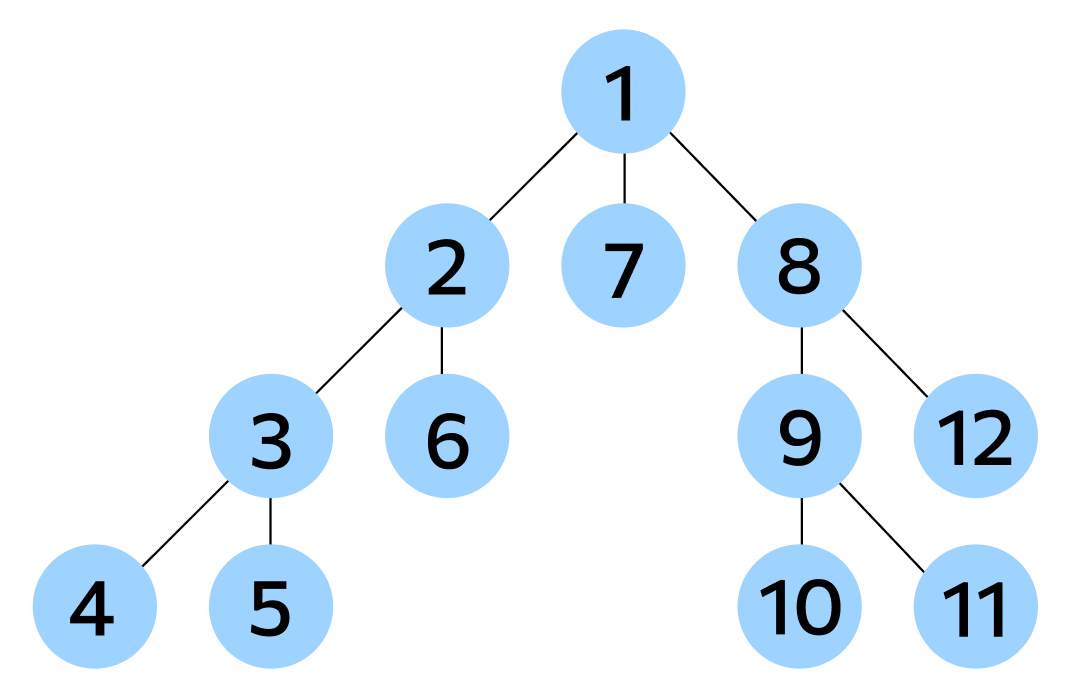
Первый шаг. Когда алгоритм начинает работу, все вершины считаются “белыми”, непосещенными. DFS начинает путь в заранее заданной вершине v и должен найти от нее путь до другой заданной вершины или же полностью составить карту графа.

Первое, что делает DFS, — красит вершину, в которой находится, в серый цвет. Это показывает, что алгоритм в ней уже был. Затем DFS проверяет соседей — вершины, которые соединены с той, где он находится.

Переход. Если какая-то из смежных вершин белая, алгоритм переходит на нее и повторяет те же действия: красит в серый, ищет соседей. Это происходит не циклически, а рекурсивно: если представить DFS как функцию, то получится, что эта функция в ходе выполнения вызывает сама себя, но для другой вершины. Поэтому сначала алгоритм работает с одним выбранным соседом и, только если упирается в тупик, возвращается обратно и пробует пройти по другому пути.

Выбор соседа происходит случайно или по заранее заданным критериям — например, это может быть самая левая или самая правая вершина. Выше мы упоминали “правило левой руки”: оно по сути является таким критерием.

Если неисследованных соседей у вершины не осталось, она красится в черный цвет как полностью посещенная.

Завершение обхода. Алгоритм завершается, если достигает нужной точки. В таком случае все вызванные “экземпляры” функции поочередно завершаются: от последнего до первого вызванного. Если задача — полностью перебрать граф, то критерий для завершения другой: все вершины должны стать черными.

Нерекурсивные реализации

Так как рекурсия отнимает много программных ресурсов, есть несколько реализаций без ее использования. Они сложнее в написании, но могут сэкономить время работы программы.

Самый простой вариант — по-особому хранить в памяти посещенные вершины. Для этого используется такая структура данных, как стек, — о ней можно прочитать в нашей статье. В стек поочередно помещаются непосещенные вершины-соседки, и тот используется как “карта” для будущих посещений. Этот способ тоже нагружает программные ресурсы, но не так сильно.

Второй вариант — хранить в стеке не сами вершины, а их номера и номера смежных с ними вершин. Это сложнее и, по сути, является имитацией так называемого стека вызовов — участка памяти, где хранятся вызванные функции. Именно его может перегрузить рекурсия.

Третий способ — реализовать сам граф на указателях: помещать в каждой вершине указатели на предыдущие и номера смежных вершин.

Это нормально, если нерекурсивные реализации кажутся вам сложными. Вы сможете разобраться с ними подробнее, когда лучше изучите программирование.

Как реализовать алгоритм DFS

Самая простая рекурсивная реализация — создать граф в виде связанного списка или другой структуры данных, а потом написать функцию для его прохождения. Как реализовать сам граф — зависит от языка программирования: обычно используются типы, позволяющие хранить множество значений. Каждый элемент такого “комплексного” типа является вершиной, а внутри вершины хранятся ссылки на другие элементы или их номера — так реализованы пути.

Сама же функция, условно названная DFS (v), довольно простая и действует по следующей логике.

1. На вход поступает белая вершина v.
2. Вершина v окрашивается в серый.
3. Ищется вершина w, смежная с v и белая.
4. Изнутри DFS (v) рекурсивно вызывается DFS (w).
5. Когда функция завершается, вершина v окрашивается в черный.

“Окрашивание” можно реализовать с помощью какой-либо переменной внутри вершины: например, значение 0 — белая, 1 — серая, и так далее.

Если сейчас часть информации кажется неочевидной — не страшно! Вы можете больше узнать про графы, рекурсию и использование DFS, если запишетесь на профессиональные курсы. Под контролем менторов вам будет легче разобраться в том, как это работает.