Системы счисления

Система счисления — это способ, которым записывают и представляют числа. Самая распространенная в нашем обществе — десятичная система, в которой используют цифры от 0 до 9. Но есть и другие системы счисления, их чаще всего используют в информатике и программировании.

Что такое система счисления

Система счисления — это способ записывать числа с помощью ограниченного набора символов и правил. Такая система позволяет выражать любые количественные значения, комбинируя несколько базовых элементов — цифры и их позиции. По сути, это универсальный «язык» чисел, который работает и в математике, и в информатике.

В математике система счисления задает, как именно записываются и читаются числа: какие символы используются, в каком порядке они стоят и как каждый из них влияет на итоговое значение. В информатике эта же идея работает на уровне данных: компьютеры хранят и обрабатывают числа в определенной системе счисления, чаще всего двоичной.

Чтобы система счисления работала, в ней есть несколько ключевых элементов:

• Основание системы. Это количество уникальных цифр, которые используются для записи чисел. Например, в десятичной системе основание равно 10 (цифры от 0 до 9), а в двоичной — 2 (цифры 0 и 1). Основание определяет, как число «растет» при увеличении разрядов: каждый следующий разряд означает умножение на основание.
• Алфавит системы. Это набор всех допустимых символов, из которых можно составлять числа. В простых системах алфавит — это сами цифры (0–9, 0–1, 0–7). В более сложных, например шестнадцатеричной, туда входят и буквы A–F, которые обозначают числа 10–15.
• Цифры. Отдельные символы из алфавита. Они не имеют большого значения сами по себе — важна их позиция в числе. В позиционных системах (а они используются практически всегда) цифра в каждом разряде умножается на основание в степени номера разряда.
• Правила записи.Это принципы, по которым цифры комбинируются. Например: «каждая цифра должна принадлежать алфавиту» и «порядок символов влияет на значение».

Такая структура позволяет системам счисления быть компактными, логичными и универсальными. Благодаря этому мы можем писать числа коротко, понимать их однозначно и передавать между людьми и компьютерами в одном формате.

Алфавит и основание системы счисления

Основание системы счисления — это число уникальных символов (цифр), которые можно использовать для записи чисел. Именно основание определяет, сколько разных значений может принимать один разряд. Например, основание 10 означает, что доступно десять цифр — от 0 до 9; основание 2 — только две: 0 и 1.

Количество символов в системе счисления всегда совпадает с её основанием. Если основание равно 8 — значит, в алфавите восемь цифр (0–7). Если основание 16 — потребуется шестнадцать символов, поэтому к цифрам 0–9 добавляются буквы A, B, C, D, E и F. Эти буквы — просто удобное обозначение чисел 10–15.

Алфавит системы счисления — это полный набор символов, которые можно использовать для записи чисел. Примеры:

• Десятичная система (основание 10): цифры 0–9
• Двоичная (основание 2): 0, 1
• Восьмеричная (основание 8): 0–7
• Шестнадцатеричная (основание 16): 0–9 и буквы A–F
• Двадцатеричная или другие экзотические системы: добавляют дополнительные буквы, чтобы расширить алфавит

Алфавиты систем счисления

Считается, что десятичная система стала основной, потому что в древности люди для подсчета предметов загибали пальцы. Пальцев у человека десять, и это стало удобной основой — люди стали считать вещи десятками.

Виды систем счисления

Системы счисления делятся на две большие группы: позиционные и непозиционные. Расскажем про все типы систем счисления, как они работают и чем они различаются.

Непозиционные

Так называют системы, в которых не важна позиция цифры в числе. Где бы цифра ни находилась, она всегда имеет одно и то же значение. Непозиционные системы счисления считаются самыми древними. Они возникли, когда люди впервые начали что-то подсчитывать и использовали для этого палочки, узелки или собственные пальцы. Позже они начали «группировать» цифры в числа, и возникли позиционные системы счисления.

Самый яркий пример — унарная система счисления, она же единичная. Ее даже иногда выделяют в отдельный вид. В ней существует только одна цифра — 1. Поэтому, например, число 5 будет записываться как 11111. Если поменять единицы местами — ничего не изменится.

Второй пример непозиционной системы, менее очевидный, — римская запись. Символ X всегда будет означать десятку, а символ V — пятерку, в каком бы месте их ни поставили. Даже в числах вроде IV, где I перед V означает «-1», I все равно будет единицей, а V — пятеркой. От положения цифры зависит только ее знак, но не ее вес.

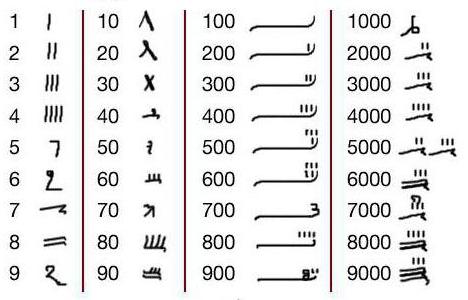
Древнеегипетская унарная система счисления основывалась на принципе прямого соответствия: одно значение — один знак. Для каждой категории чисел у египтян был свой символ: единицу обозначали вертикальной чертой, десяток — U-образным «крюком», сотню — спиралью, тысячу — цветком лотоса и так далее. Чтобы записать число, эти символы просто повторяли нужное количество раз, группируя их по значению.

Система была непозиционной: порядок знаков не менял величину, а сложные числа выглядели как набор повторяющихся фигур. Такой способ записи был наглядным и понятным, но занимал много места и требовал времени, особенно при больших числах.

Непозиционные системы используются редко. В них нет нуля, нет дробных чисел и других инструментов, которые бывают важны в современных вычислениях.

Позиционные

Сюда относятся десятичная, двоичная и большинство других современных систем счисления. В таких системах есть разряды, зависящие от позиции. Значение цифры меняется в зависимости от того, в каком месте она находится. Например, в числе 15 пятерка означает «пять единиц», а в числе 54 — «пять десятков».

Примеры позиционных систем счисления включают:

• Десятичную систему (основание 10) — самая привычная в повседневной жизни; значение цифры зависит от ее разряда (единицы, десятки, сотни).
• Двоичную систему (основание 2) — используется в компьютерах; числа записываются с помощью 0 и 1, а каждый разряд отражает степень двойки.
• Восьмеричную систему (основание 8) — применялась в ранних компьютерах и до сих пор встречается в низкоуровневом программировании.
• Шестнадцатеричную систему (основание 16) — удобна для компактной записи двоичных данных; использует цифры 0–9 и буквы A–F.
• Троичную систему (основание 3) — менее распространена, но применяется в теоретических моделях вычислений и кодировании.

Позиционные системы счисления удобны, потому что значение цифры в них зависит от ее места в записи числа. Это позволяет компактно выражать даже очень большие значения, заменяя длинные повторяющиеся знаки ограниченным набором разрядов.

Благодаря позиционности легко выполнять арифметические операции — сложение, вычитание, умножение и деление превращаются в формальные алгоритмы, которые можно автоматизировать. Именно поэтому такие системы стали основой современной математики и информатики: они экономят пространство, ускоряют вычисления и подходят как для ручного счета, так и для работы компьютеров.

В целом такие системы используют чаще, чем непозиционные, за исключением некоторых узких сфер. Например, в некоторых комбинаторных расчетах используют непозиционную биномиальную систему — она основана на биноме Ньютона.

Виды позиционных систем счисления

Позиционные системы счисления в свою очередь делятся на две категории — однородные и смешанные.

• Однородные системы — такие, в которых правила записи одинаковые для всех разрядов. В каждом разряде можно использовать один и тот же алфавит. Десятичная система именно такая. И в единицах, и в десятках, и в сотнях или тысячах мы пользуемся цифрами от 0 до 9.
• Смешанные системы — такие, где у разных разрядов различаются правила записи или даже основание. Например, система подсчета времени. У разряда «минуты» основание 60, и минуты можно обозначать числами от 0 до 59. На 60 число переходит в разряд «часы». А у разряда «часы» основание 24, и количество часов можно обозначать цифрами от 0 до 23. На 24 число переходит в разряд «сутки». И так далее.

Смешанные системы используют реже, чем однородные — исключением можно назвать разве что подсчет времени. Но, например, смешанной системой считается факториальная: 2! — это 2, 3! — уже 6, а 4! — 24. Видно, что основание меняется, а сама система нелинейная.

Основные позиционные системы счисления

Практически все системы, которые используют в компьютерной технике, — позиционные и однородные. Как правило, у них четное основание, которое соответствует какой-либо из степеней двойки. Это связано с особенностями хранения данных в памяти компьютера. Рассмотрим три наиболее популярных в информатике системы счисления: двоичную, восьмеричную и шестнадцатеричную.

Двоичная система счисления

Это система с основанием 2 и алфавитом, который состоит всего из двух цифр — 0 и 1. Необходимость использовать двоичную систему появилась из-за того, как компьютеры представляют информацию: в виде бит. Бит может принимать только значение «0» или «1» — «тут нет единицы информации» или «тут есть единица информации».

• 0 означает ноль, отсутствие информации.
• 1 означает единицу, например записанную в какую-то ячейку памяти.
• Цифры 2 в системе нет. Если число достигает значения 2, оно переходит в другой разряд и записывается как 10 — одна двойка и ноль единиц. Соответственно, число 3 будет записываться как 11 — одна двойка и одна единица.
• Дальше разряды увеличиваются по тому же принципу. Число 4 — это 100, то есть две двойки и 0 единиц. Число 8 — 1000, и так далее. Каждая новая степень двойки — новый разряд.

Напрямую работать с двоичным, или бинарным кодом разработчикам приходится редко. Но для общего понимания важно знать, как устроена двоичная система. Именно в таком виде на самом глубоком уровне хранятся данные в компьютере — как последовательности из нулей и единиц.

Восьмеричная система счисления

Эту систему используют чуть реже, чем двоичную и шестнадцатеричную. Чаще всего ее упоминание можно встретить при работе с низкоуровневыми языками программирования, которые близки к «железу» и способны обрабатывать данные напрямую. Компьютеры объединяют части бинарного кода в блоки по 8 двоичных цифр — байты. Отсюда появилась и необходимость работать с восьмеричной системой.

• Основа системы счисления — 8. Это значит, что от 0 до 7 цифры идут как обычно, а когда число доходит до 8, начинается другой разряд и число записывается как 10.
• Соответственно, число 9 будет записываться как 11, а число 10 — как 12.
• Число 16 в восьмеричной системе записывается как 20, потому что шестнадцать — это два раза по восемь. И так далее.
• Число 64 в восьмеричной системе будет выглядеть как 100, потому что это восемь раз по восемь.

Шестнадцатеричная система счисления

С этой системой счисления сталкиваются не только разработчики, но и, например, дизайнеры — в ней кодируются цвета RGB. Еще в этой системе записываются коды символов во многих кодировках. Основание шестнадцатеричной системы — число 16. Оно больше десяти, поэтому в алфавите появляются дополнительные цифры, которые обозначают буквами.

• От 0 до 9 цифры идут как обычно. Но на десяти разряд еще не меняется, поэтому для обозначения десятки нужна новая цифра. В качестве этой «цифры» используют латинскую букву A.
• Соответственно, «цифра» 11 — это B, 12 — C, и так далее до F, которая обозначает «цифру» 15.
• Когда счет доходит до шестнадцати, разряд меняется. Следующее число после F в шестнадцатеричной системе — 10.
• Числа в шестнадцатеричной системе выглядят меньше, чем в десятичной. Например, 100 в шестнадцатеричной системе — это 16 раз по 16, то есть 16 в квадрате. В десятичной системе это число 256.
• Цифры в виде букв могут встречаться в начале, конце или середине числа. Например, 1A — это 26. Единица обозначает один раз по шестнадцать, а A — «цифру» десять.

Как записывают числа в разных система счисления

Одно и то же число может иметь разные записи, потому что каждая система счисления использует свой набор символов (алфавит) и свое основание — правило, по которому растет значение разрядов. Число как абстрактная величина остается тем же, но способ его записи меняется в зависимости от того, какие «строительные блоки» доступны.

В десятичной системе мы используем десять цифр (0–9), и значение каждого разряда определяется степенью числа 10. В двоичной системе доступны только 0 и 1, поэтому любое число раскладывается на степени двойки. В шестнадцатеричной — на степени 16, а цифры дополняются буквами A–F. Из-за этих особенностей одни системы дают длинные записи (двоичная), другие — более компактные (шестнадцатеричная). Поэтому число 25 будет выглядеть как 25 в десятичной системе, как 11001 в двоичной и как 19 в шестнадцатеричной — смысл один, меняется лишь «язык», на котором оно записано.

Как переводить из одной системы счисления в другую

Общий принцип перевода чисел из одной системы счисления в другую основан на промежуточном представлении числа в десятичной форме.

Сначала число «раскладывают» по разрядам: каждую цифру умножают на основание системы и степень, соответствующую её позиции, а затем складывают — так получают десятичное значение. После этого число переводят в целевую систему: последовательно делят десятичное значение на новое основание и фиксируют остатки, которые становятся цифрами результата (записывают их в обратном порядке).

Для дробных частей используют умножение на основание и выделение целой части. Этот подход универсален и позволяет переводить числа между любыми позиционными системами.

Приведем несколько примеров алгоритмов, которые помогают быстро и удобно перевести число из одной системы счисления в другую.

Перевод из десятичной системы в другую

Алгоритм такой: нужно шаг за шагом делить число в десятичной системе на основание той системы, в которую мы его переводим. Это делается до тех пор, пока исходное число не станет равным 0. Остаток от деления — это цифра в новом числе. Остатки записывают начиная с последнего и заканчивая первым и так получают число в нужной системе счисления.

Например, число 13 в десятичной системе мы хотим перевести в двоичную. 

1. Мы делим 13 на 2 — получаем 6, остаток 1. 
2. Потом делим 6 на 2 — получаем 3, остаток 0. 
3. Потом делим 3 на 2 — получаем 1, остаток 1. 
4. Потом делим 1 на 2 — получаем 0, остаток 1.
5. Исходное число стало равным нулю — значит, мы закончили. Теперь записываем остатки в обратном порядке: 1, 1, 0, 1. Выходит число в двоичной системе — 1101.

Перевод из любой системы в десятичную

Способ немного более запутанный, но на самом деле несложный. Нужно взять число в нужной системе счисления и пронумеровать его разряды с конца, начиная с 0. Самая последняя цифра — нулевой разряд, вторая с конца — первый разряд, и так далее. Затем каждую из цифр нужно умножить на основание системы счисления, которое предварительно возвели в степень номера разряда. Полученные числа нужно сложить.

Например, есть число 93 в шестнадцатеричной системе счисления. Мы хотим перевести его в десятичную.

1. Нумеруем разряды числа. У цифры 9 номер 1, у цифры 3 номер 0.
2. Основание системы — 16. 16 в первой степени — это 16, а 16 в нулевой степени — это 1.
3. Цифру 9 мы умножаем на 16, а цифру 3 — на 1. Получаем числа 144 и 3.
4. Складываем 144 и 3, получаем число 147 в десятичной системе счисления.

Перевод в восьмеричную систему счисления

Начиная с правого конца, делим двоичное число на триады: на группы по 3 цифры. Добавляем слева недостающие нули, чтобы все группы были трехзначными.

Затем заменяем каждую триаду на соответствующую восьмеричную цифру: в этом поможет таблица соответствия между триадами и восьмеричными цифрами.

Записываем полученные восьмеричные цифры слева направо — итоговое число в восьмеричной системе готово.

Пример:

Хотим преобразовать число 1101011010 в восьмеричную систему.

Решение:

1. Делим на триады: 011 010 110 10
2. Заменяем триады: 3 2 6 2
3. Соединяем цифры: 3262

Ответ: 3262 восьмеричное = 1101011010 двоичное.

Перевод в шестнадцатеричную систему счисления

Начиная с правого конца, делим число на тетрады: группы по 4 цифры. Добавляем слева недостающие нули, чтобы все группы были четырехзначными.

Заменяем каждую тетраду на соответствующую шестнадцатеричную цифру: в этом поможет таблица соответствия между тетрадами и шестнадцатеричными цифрами.

Соединяем шестнадцатеричные цифры слева направо,— итоговое число в шестнадцатеричной системе готово.

Пример:

Хотим преобразовать число 101011101010111101010101111110111010101110111010101011101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010101010

Решение:

1. Делим число на тетрады
2. Заменяем тетрады: A 5 B A 5 F E B C E A 5 6 7 4 2 E A 5 6 7 4 2 E A 5 6 7 4 2 E A 5 6 …
3. Соединяем цифры: A5B5F7EBCE56742EA56742EA56742EA56742E

Таблица степеней оснований систем счисления

Степень (разряд)	Двоичная система (2ⁿ)	Восьмеричная (8ⁿ)	Десятичная (10ⁿ)	Шестнадцатеричная (16ⁿ)
n = 0	1	1	1	1
n = 1	2	8	10	16
n = 2	4	64	100	256
n = 3	8	512	1000	4096
n = 4	16	4096	10 000	65 536
n = 5	32	32 768	100 000	1 048 576
n = 6	64	262 144	1 000 000	16 777 216
n = 7	128	2 097 152	10 000 000	268 435 456
n = 8	256	16 777 216	100 000 000	4 294 967 296

Онлайн-сервисы для перевода чисел между системами счисления

Перевести числа быстро и удобно можно при помощи специальных сервисов. Делимся подборкой.

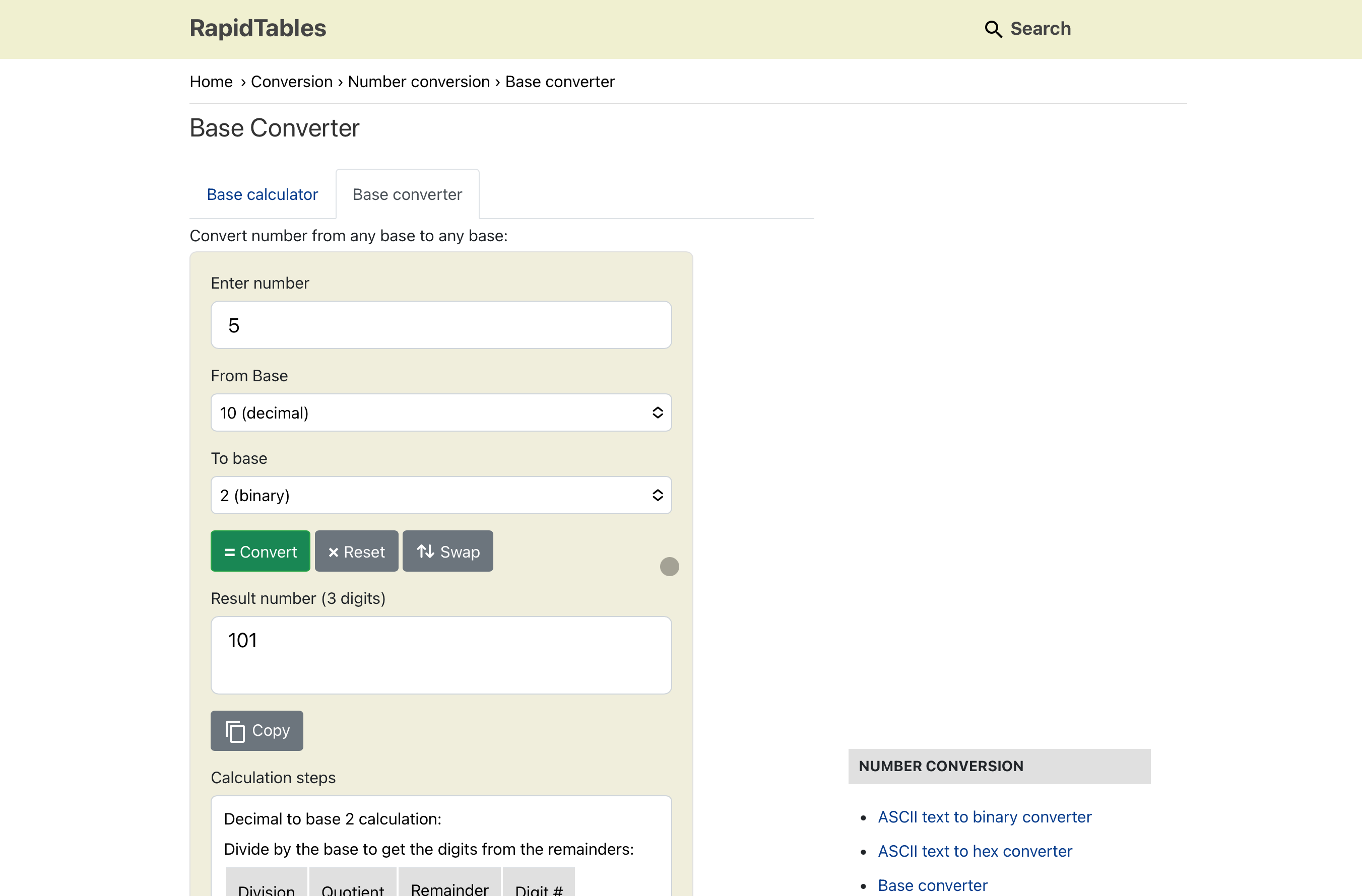
• RapidTables. Простой конвертер, показывает результат сразу в нескольких системах.
• OnlineConversion. Минималистичный сервис для быстрых конверсий.
• CyberChef. Мощный инструмент для работы с числами, кодировками и форматами данных.
• Math is Fun. Учебный инструмент, показывающий промежуточные шаги перевода.

Где и зачем используют системы счисления

По сути, система счисления — это просто способ, которым записывают число. Одно и то же число в разных системах может выглядеть по-разному, но при этом его суть останется прежней.

Исторически системы счисления появились задолго до компьютеров. Древние цивилизации создавали свои способы записи чисел: египтяне использовали унарную и иератическую систему, шумеры и вавилоняне применяли шестидесятеричную, римляне — непозиционную буквенную запись.

Эти системы позволяли вести учет, торговать, строить календари и планировать хозяйственные процессы. Современные позиционные системы выросли из этих древних практик и стали основой математики и цифровых технологий.

Где используются системы счисления

Системы счисления нужны везде, где требуется передавать, хранить или обрабатывать числовую информацию. В математике они позволяют компактно записывать большие числа и выполнять арифметические операции по универсальным правилам. В информатике система счисления — это основа представления данных: компьютеры работают с двоичным кодом, используют шестнадцатеричную запись для удобного отображения байтов и опираются на позиционный принцип при вычислениях.

В программировании системы счисления применяются для работы с памятью, адресами, машинными кодами и числами разных типов. Двоичная система лежит в основе логики процессоров, восьмеричная и шестнадцатеричная — удобны для чтения и записи низкоуровневых данных. Разработчики используют их при работе с битовыми масками, сетевыми протоколами, цветами в веб-разработке (HEX), шифрованием и декодированием данных.

Вот несколько примеров:

• цвета в формате RGB описывают числами в шестнадцатеричной системе. Например, белый — это #FFFFFF, а черный — #000000. Да, F в этом случае — тоже цифра;
• символы в разных кодировках, например ASCII или UTF-8, тоже описывают числами в шестнадцатеричном формате. Иногда их же представляют в виде двоичных чисел;
• в некоторых языках программирования, особенно в низкоуровневых вроде ассемблера, приходится работать с данными на уровне бит и байт — а способы хранения данных тесно связаны с двоичной и восьмеричной системами счисления.

Разработчики, которые имеют дело только с высокоуровневыми языками вроде JavaScript, как правило, редко сталкиваются с системами счисления. Но понимать, как они устроены, айтишнику все равно нужно — чтобы лучше разбираться в том, как функционируют компьютеры.

Интересные факты о системах счисления

Почему компьютер «думает» двоично

Компьютеры используют двоичную систему, потому что электронные схемы надежно различают только два устойчивых состояния: есть сигнал или нет, 1 или 0. Такое кодирование минимизирует ошибки, упрощает конструкцию микросхем и делает операции быстрыми и предсказуемыми. Любые числа, символы и команды процессор в итоге сводит к последовательностям битов — это универсальный «алфавит» цифровой техники.

Почему шестнадцатеричная система удобнее в программировании

Шестнадцатеричная система — компактный способ представить те же двоичные данные. Один шестнадцатеричный символ соответствует ровно четырем битам, поэтому длинные двоичные последовательности превращаются в более короткие и удобные для чтения записи. Например, 11110000 в шестнадцатеричной форме — это просто F0. Такой формат используют при работе с памятью, байт-кодами, цветовыми значениями (HEX), сетевыми протоколами и отладкой низкоуровневых процессов.

Почему десятичная — не единственно возможная

Десятичная система стала привычной не потому, что она «правильная», а по историческим причинам: людям удобно было считать на пальцах. Но математика допускает любое основание — 2, 8, 12, 60 или 36 — и у каждой системы есть свои преимущества. Шестидесятеричная система древних вавилонян до сих пор живет в часах и углах, двоичная и шестнадцатеричная — в компьютерах, троичная — в теоретических моделях вычислений. Основание — это просто инструмент, а выбор системы зависит от задач, которые нужно решать.

Как изучить системы счисления

Часто системы счисления проходят в школе на уроках информатики или математики. Но не всегда эту тему включают в программу. Тем не менее это одно из базовых понятий компьютерных наук — для успешной карьеры в IT лучше понимать, что такое системы счисления и как они работают.

Освоить системы счисления проще, если рассматривать их не как абстракцию, а как разные способы «говорить» о числе. Начать стоит с позиционного принципа: понять, как разряды зависят от основания и почему число раскладывается на степени. Полезно потренироваться переводить числа между системами — сначала вручную, затем с помощью тренажёров. Важно не просто запомнить алгоритмы, а увидеть логику: почему двоичная запись длиннее, как шестнадцатеричная группирует биты, чем отличается унарная или римская система.

Советы для студентов:

• Освойте перевод в десятичную систему — это универсальный «мост» между основаниями.
• Разбирайте примеры пошагово: записывайте степени, выделяйте разряды.
• Потренируйтесь в обоих направлениях — из десятичной и обратно.
• Используйте визуализацию: таблицы степеней, бинарные блоки по 4 бита.
• Сравнивайте системы между собой — это помогает лучше понять их структуру.

Полезные материалы и инструменты:

• Тренажёры перевода чисел: RapidTables, Math is Fun, CalculatorSoup.
• Курсы по основам программирования и информатики, где работа с числами — обязательный модуль.
• Практика на задачах: переводы, вычисления, работа с байтовыми значениями.

Системы счисления быстро становятся понятными, если регулярно практиковаться и разбирать реальные примеры — от машинного кода до цвета в HEX.

Коротко о главном: системы счисления

Система счисления — это способ записывать числа с помощью набора символов и правил. У каждой системы есть основание — количество доступных цифр. Например, 10 в десятичной, 2 в двоичной, 16 в шестнадцатеричной.

Алфавит системы — это набор символов, которые разрешено использовать. В разных системах это могут быть цифры или комбинация цифр и букв. Одно и то же число может выглядеть по-разному в зависимости от системы, но его значение остается одинаковым.

Системы бывают позиционными (двоичная, десятичная, шестнадцатеричная) и непозиционными (римская, унарная). В информатике широко используются системы со степенями двойки, потому что они соответствуют принципам работы компьютеров.

Перевод чисел между системами основан на двух шагах:

1. Представление числа как суммы разрядов (для перевода в десятичную).
2. Деление на основание с фиксацией остатков (для перевода из десятичной).

Системы счисления — фундаментальный инструмент для работы с числами. Понимание принципов помогает в программировании, работе с данными и разборе цифровых форматов.